P.1 Assess Your Understanding
Concepts and Vocabulary
Question
If \(f\) is a function defined by \(y=f ( x ) \), then \(x\) is called the _____ variable and \(y\) is the _____ variable.
Question
True or False The independent variable is sometimes referred to as the argument of the function.
Question
True or False If no domain is specified for a function \(f,\) then the domain of \(f\) is taken to be the set of all real numbers.
Question
True or False The domain of the function \(f ( x ) =\dfrac{3 ( x^{2}-1 ) }{x-1}\) is \( \{ x|x\neq \pm 1 \} .\)
Question
True or False A function can have more than one \(y\)-intercept.
Question
A set of points in the \(xy\)-plane is the graph of a function if and only if every _____ line intersects the graph in at most one point.
Question
If the point \(( 5,-3 ) \) is on the graph of \(f\), then \(f(\) _____ \()\) \(=\) _____.
Question
Find \(a\) so that the point \(( -1,2 ) \) is on the graph of \(f( x ) =ax^{2}+4\).
Question
Multiple Choice A function \(f\) is [(a) increasing, (b) decreasing, (c) nonincreasing, (d) nondecreasing, (e) constant] on an interval \(I\) if, for any choice of \(x_{1}\) and \(x_{2}\) in \(I,\) with \(x_{1}<x_{2}\), then \(f( x_{1}) <f( x_{2}) \).
Question
Multiple Choice A function \(f\) is [(a) even, (b) odd, (c) neither even nor odd] if for every number \(x\) in its domain, the number \(-x\) is also in the domain and \(f( -x) =f( x) \). A function \(f\) is [(a) even, (b) odd, (c) neither even nor odd] if for every number \(x\) in its domain, the number \(-x\) is also in the domain and \(f( -x) =-f( x) \).
13
Question
True or False Even functions have graphs that are symmetric with respect to the origin.
Question
The average rate of change of \(f( x) =2x^{3}-3\) from \(0\) to \(2\) is _____.
Practice Problems
In Problems 13–16, for each function find:
- \(f ( 0) \)
- \(f ( -x) \)
- \(-f ( x) \)
- \(f (x+1) \)
- \(f ( x+h) \)
Question
\(f( x) =3x^{2}+2x-4\)
Question
\(f( x) =\dfrac{x}{x^{2}+1}\)
Question
\(f(x) =\vert x\vert +4 \)
Question
\(f( x) = \sqrt{3-x}\)
In Problems 17–22, find the domain of each function.
Question
\(f( x) =x^{3}-1\)
Question
\(f( x) =\dfrac{x}{x^{2}+1}\)
Question
\(v( t) = \sqrt{t^{2}-9}\)
Question
\(g( x) = \sqrt{\dfrac{2}{x-1}}\)
Question
\(h( x) =\dfrac{x+2}{x^{3}-4x}\)
Question
\(s( t) =\dfrac{ \sqrt{t+1}}{t-5}\)
In Problems 23–28, find the difference quotient of f. That is, find \(\dfrac{f ( x+h) -f ( x) }{h}\), \(h\neq 0\).
Question
\(f ( x) =-3x+1\)
Question
\(f ( x) =\dfrac{1}{x+3}\)
Question
\(f ( x) = \sqrt{x+7}\)
Question
\(f ( x) =\dfrac{2}{ \sqrt{x+7}}\)
Question
\(f ( x) =x^{2}+2x\)
Question
\(f ( x) = ( 2x+3) ^{2}\)
In Problems 29–32, determine whether the graph is that of a function by using the Vertical-line Test. If it is, use the graph to find
- the domain and range
- the intercepts, if any
- any symmetry with respect to the x-axis, y-axis, or the origin.
Question
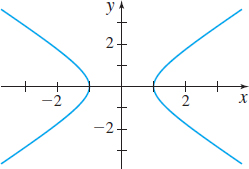
Question

Question
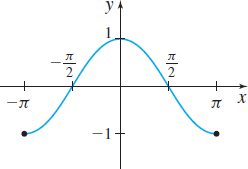
Question
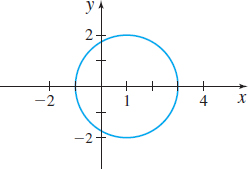
In Problems 33–36, for each piecewise-defined function:
- Find \(f ( -1 )\), \(f ( 0 ) \), \(f ( 1 ) \) and \(f ( 8 )\).
- Graph \(f\).
- Find the domain, range, and intercepts of \(f.\)
Question
\(f( x) =\left\{ \begin{array}{l@{\qquad}l@{\quad}l} x+3 & {\rm if}& -2\leq x<1 \\ 5 & {\rm if}& x=1 \\ -x+2 & {\rm if}& x>1 \end{array} \right. \)
Question
\(f( x) =\left\{ \begin{array}{l@{\qquad}l@{\quad}l} 2x+5 & {\rm if} & -3\leq x<0 \\ -3 & {\rm if} & x=0 \\ -5x & {\rm if} & x>0 \end{array} \right. \)
Question
\(f( x) =\left\{ \begin{array}{l@{\qquad}l@{\quad}l} 1+x & {\rm if} & x<0 \\ x^{2} & {\rm if} & x\geq 0 \end{array} \right.\)
Question
\(f( x) =\left\{ \begin{array}{l@{\qquad}l@{\quad}l} \dfrac{1}{x} & {\rm if} & x<0 \\ \sqrt[3]{x} & {\rm if} & x\geq 0 \end{array} \right.\)
In Problems 37–54, use the graph of the function \(f\) to answer the following questions.
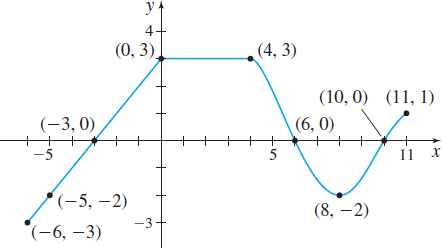
Question
Find \(f ( 0) \) and \(f( -6)\).
Question
Is \(f ( 3) \) positive or negative?
Question
Is \(f ( -4) \) positive or negative?
Question
For what values of \(x\) is \(f ( x) =0\)?
Question
For what values of \(x\) is \(f ( x) >0\)?
Question
What is the domain of \(f\)?
Question
What is the range of \(f\)?
Question
What are the \(x\)-intercepts?
Question
What is the \(y\)-intercept?
Question
How often does the line \(y=\dfrac{1}{2}\) intersect the graph?
Question
How often does the line \(x=5\) intersect the graph?
Question
For what values of \(x\) does \(f( x) =3\)?
Question
For what values of \(x\) does \(f( x) =-2\)?
Question
On what interval(s) is the function \(f\) increasing?
Question
On what interval(s) is the function \(f\) decreasing?
Question
On what interval(s) is the function \(f\) constant?
Question
On what interval(s) is the function \(f\) nonincreasing?
Question
On what interval(s) is the function \(f\) nondecreasing?
14
In Problems 55–60, answer the questions about the function \[ g( x) =\dfrac{x+2}{x-6}. \]
Question
What is the domain of \(g\)?
Question
Is the point \(( 3,14) \) on the graph of \(g\)?
Question
If \(x=4\), what is \(g( x) \)? What is the corresponding point on the graph of \(g\)?
Question
If \(g( x) =2\), what is \(x\)? What is(are) the corresponding point(s) on the graph of \(g\)?
Question
List the \(x\)-intercepts, if any, of the graph of \(g\).
Question
What is the \(y\)-intercept, if there is one, of the graph of \(g\)?
In Problems 61–64, determine whether the function is even, odd, or neither. Then determine whether its graph is symmetric with respect to the \(y\)-axis, the origin, or neither.
Question
\(h( x) =\dfrac{x}{x^{2}-1}\)
Question
\(f( x) =\sqrt[3]{3x^{2}+1} \)
Question
\(G( x) = \sqrt{x}\)
Question
\(F( x) =\dfrac{2x}{\vert x\vert }\)
Question
Find the average rate of change of \(f(x) =-2x^{2}+4\):
- From \(1\) to \(2\)
- From \(1\) to \(3\)
- From \(1\) to \(4\)
- From \(1\) to \(x\), \(x\neq 1\)
Question
Find the average rate of change of \(s( t) =20-0.8t^{2}\):
- From \(1\) to \(4\)
- From \(1\) to \(3\)
- From \(1\) to \(2\)
- From \(1\) to \(t\), \(t\neq 1\)
In Problems 67–72, the graph of a piecewise-defined function is given. Write a definition for each piecewise-defined function. Then state the domain and the range of the function.
Question
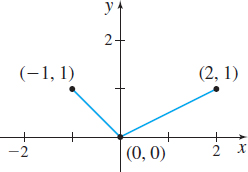
Question
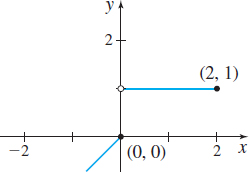
Question
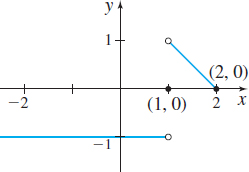
Question
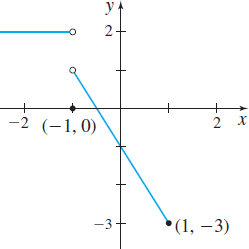
Question
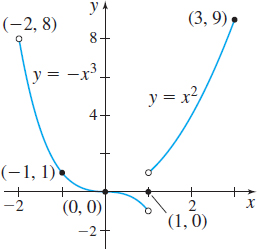
Question
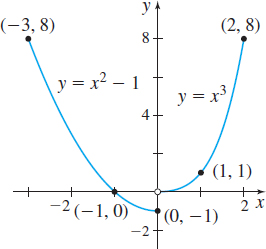
Question
The monthly cost \(C\), in dollars, of manufacturing \(x\) road bikes is given by the function \[ C( x) =0.004x^{3}-0.6x^{2}+250x+100{,}500 \]
- Find the average rate of change of the cost \(C\) of manufacturing from \( 100\) to \(101\) road bikes.
- Find the average rate of change of the cost \(C\) of manufacturing from \( 500\) to \(501\) road bikes.
- Interpret the results from parts (a) and (b).
Question
The weekly cost in dollars to produce \(x\) tons of steel is given by the function \[ C( x) =\dfrac{1}{10}x^{2}+5x+1500 \]
- Find the average rate of change of the cost \(C\) of producing from \(500\) to \(501\) tons of steel.
- Find the average rate of change of the cost \(C\) of producing from \(1000\) to \(1001\) tons of steel.
- Interpret the results from parts (a) and (b).
