P.2 Assess Your Understanding
Concepts and Vocabulary
Question
Multiple Choice The function \(f ( x) =x^{2}\) is [(a) increasing, (b) decreasing, (c) neither] on the interval \(( 0,\infty ) \).
Question
True or False The floor function \(f( x) =\lfloor x\rfloor \) is an example of a step function.
Question
True or False The cube function is odd and is increasing on the interval \(( -\infty ,\infty ) \).
Question
True or False The cube root function is odd and is decreasing on the interval \(( -\infty ,\infty ) \).
Question
True or False The domain and the range of the reciprocal function are all real numbers.
Question
A number \(r\) for which \(f( r) =0\) is called a(n) _____ of the function \(f\).
Question
Multiple Choice If \(r\) is a zero of even multiplicity of a function \(f\), the graph of \(f\) [(a) crosses, (b) touches, (c) doesn't intersect] the \(x\)-axis at \(r\).
Question
True or False The \(x\)-intercepts of the graph of a polynomial function are called zeros of the function.
Question
True or False The function \(f( x) =\left[ x+\sqrt[5]{x^{2}-\pi }\right] ^{2/3}\) is an algebraic function.
Question
True or False The domain of every rational function is the set of all real numbers.
Practice Problems
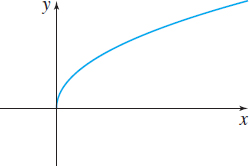
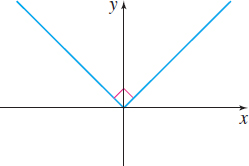
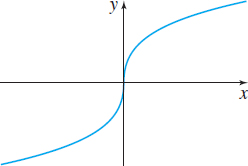
In Problems 11–18, match each graph to its function:
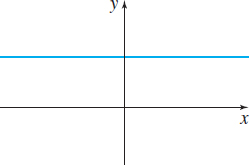
- Constant function
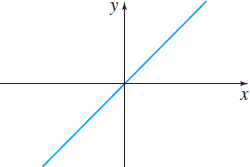
- Identity function
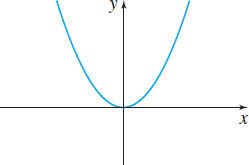
- Square function
- Cube function
- Square root function
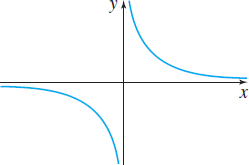
- Reciprocal function
- Absolute value function
- Cube root function
Question

Question
Question
Question
23
Question
Question
Question
Question
Question
If \(f( x) = \lfloor 2x\rfloor \), find
- \(f( 1.2) \),
- \(f( 1.6) \),
- \(f( -1.8) \).
Question
If \(f( x) =\left\lceil \dfrac{x}{2}\right\rceil \), find
- \(f( 1.2)\),
- \(f ( 1.6) \),
- \(f ( -1.8) \).
In Problems 21 and 22, for each polynomial function \(f\):
- List each real zero and its multiplicity.
- Find the \(x\)- and \(y\)-intercepts of the graph of \(f\).
- Determine whether the graph of \(f\) crosses or touches the \(x\)-axis at each \(x\)-intercept.
Question
\(f( x) =3( x-7) (x+4) ^{3}\)
Question
\(f( x)=4x( x^{2}+1) ( x-2) ^{3}\)
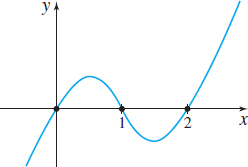
In Problems 23 and 24, decide which of the polynomial functions in the list might have the given graph. (More than one answer is possible.)
Question
- \(f( x) =-4x ( x-1) ( x-2)\)
- \(f( x) =x^{2} ( x-1) ^{2} ( x-2)\)
- \(f( x) =3x( x-1) ( x-2)\)
- \(f( x) =x( x-1) ^{2}( x-2) ^{2}\)
- \(f( x) =x^{3}( x-1) ( x-2)\)
- \(f( x) =-x ( 1-x ) ( x-2 ) \)
Question
- \(f( x) =2x^{3}( x-1) ( x-2) ^{2}\)
- \(f( x) =x^{2}( x-1) ( x-2) \)
- \(f( x) =x^{3}( x-1) ^{2}( x-2)\)
- \(f( x) =x^{2} ( x-1 ) ^{2} ( x-2 ) ^{2}\)
- \(f( x) =5x( x-1) ^{2}( x-2)\)
- \(f( x) =-2x ( x-1) ^{2} ( 2-x) \)
In Problems 25–28, find the domain and the intercepts of each rational function.
Question
\(R( x) =\dfrac{5x^{2}}{x+3}\)
Question
\(H( x) =\dfrac{-4x^{2}}{( x-2) ( x+4) }\)
Question
\(R( x) =\dfrac{3x^{2}-x}{x^{2}+4}\)
Question
\(R( x) =\dfrac{3(x^{2}-x-6) }{4( x^{2}-9) }\)
Question
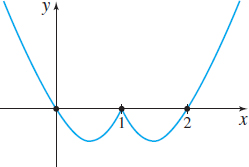
Constructing a Model The rectangle shown in the figure has one corner in quadrant I on the graph of \(y=16-x^{2}\), another corner at the origin, and corners on both the positive \(y\)-axis and the positive \(x\)-axis. As the corner on \(y=16-x^{2}\) changes, a variety of rectangles are obtained.
- Express the area \(A\) of the rectangles as a function of \(x\).
- What is the domain of \(A\)?
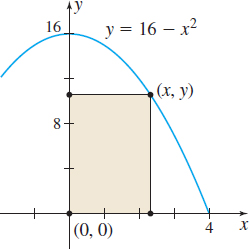
Question
Constructing a Model The rectangle shown in the figure is inscribed in a semicircle of radius \(2\). Let \(P=( x,y) \) be the point in quadrant I that is a vertex of the rectangle and is on the circle. As the point \(( x,y) \) on the circle changes, a variety of rectangles are obtained.
- Express the area \(A\) of the rectangles as a function of \(x\).
- Express the perimeter \(p\) of the rectangles as a function of \(x\).
Question
![]() Height of a Ball A ballplayer throws a ball at an inclination of \(45^\circ\) to the horizontal. The following data represent the height \(h\) (in feet) of the ball at the instant that it has traveled \(x\) feet horizontally:
Height of a Ball A ballplayer throws a ball at an inclination of \(45^\circ\) to the horizontal. The following data represent the height \(h\) (in feet) of the ball at the instant that it has traveled \(x\) feet horizontally:
| Distance, \(x\) | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| Height, \(h\) | 25 | 40 | 55 | 65 | 71 | 77 | 77 | 75 | 71 | 64 |
- Draw a scatter plot of the data. Comment on the type of relation that may exist between the two variables.
- Use technology to verify that the quadratic function of best fit to these data is \[ h( x) =-0.0037x^{2}+1.03x+5.7 \] Use this function to determine the horizontal distance the ball travels before it hits the ground.
- Approximate the height of the ball when it has traveled 10 feet.
Question
![]() Educational Attainment The following data represent the percentage of the U.S. population whose age is \(x\) (in years) who did not have a high school diploma as of January 2011:
Educational Attainment The following data represent the percentage of the U.S. population whose age is \(x\) (in years) who did not have a high school diploma as of January 2011:
| Age, \(x\) | \(30\) | \(40\) | \(50\) | \(60\) | \(70\) | \(80\) |
| Percentage without a High School Diploma, \(P\) | \(11.6\) | \(11.7\) | \(10.4\) | \(10.4\) | \(17.0\) | \(24.6\) |
Source: U.S. Census Bureau.
- Draw a scatter plot of the data, treating age as the independent variable. Comment on the type of relation that may exist between the two variables.
- Use technology to verify that the cubic function of best fit to these data is \[ P( x) =0.00026x^{3}-0.0303x^{2}+1.0877x-0.5071 \]
- Use this model to predict the percentage of 35-year-olds who do not have a high school diploma.
