P.3 Operations on Functions; Graphing Techniques
24
OBJECTIVES
When you finish this section, you should be able to:
- Form the sum, difference, product, and quotient of two functions (p. 24)
- Form a composite function (p. 25)
- Transform the graph of a function with vertical and horizontal shifts (p. 27)
- Transform the graph of a function with compressions and stretches (p. 29)
- Transform the graph of a function by reflecting it about the \(x\)-axis and the \(y\)-axis (p. 30)
1 Form the Sum, Difference, Product, and Quotient of Two Functions
Functions, like numbers, can be added, subtracted, multiplied, and divided. For example, the polynomial function \(F( x) =x^{2}+4x\) is the sum of the two functions \(f( x) =x^{2}\) and \(g( x) =4x.\) The rational function \(R( x) =\dfrac{x^{2}}{x^{3}-1}\), \(x\neq 1\), is the quotient of the two functions \(f( x) =x^{2}\) and \(g( x) =x^{3}-1\).
spanDEFINITIONspan Operations on Functions
If \(f\) and \(g\) are two functions, their sum, \(f+g\); their difference, \(f-g\); their product, \(f\cdot g\); and their quotient, \(\dfrac{f}{g}\), are defined by
- Sum: \( (f+g) ( x) =f( x) +g( x)\)
- Difference: \( (f-g)( x) = f( x) -g( x)\)
- Product: \((f\cdot g) ( x) = f( x) \cdot g( x)\)
- Quotient: \(\left(\dfrac{f}{g}\right) ( x) =\dfrac{f( x) }{g( x) },\ \ g( x) \neq 0\)
For every operation except division, the domain of the resulting function consists of the intersection of the domains of \(f\) and \(g.\) The domain of a quotient \(\dfrac{f}{g}\) consists of the numbers \(x\) that are common to the domains of both \(f\) and \(g\), but excludes the numbers \(x\) for which \( g( x) =0.\)
Forming the Sum, Difference, Product, and Quotient of Two Functions
Let \(f\) and \(g\) be two functions defined as \[ f( x) =\sqrt{x-1}\qquad\hbox{and}\qquad g( x) =\sqrt{4-x} \] Find the following functions and determine their domain:
- \(( f+g) ( x)\)
- \((f-g) ( x)\)
- \((f\cdot g)( x)\)
- \(\left( \dfrac{f}{g}\!\right) ( x)\)
Solution The domain of \(f\) is \(\{ x|x\geq 1\} \), and the domain of \(g\) is \(\{ x |x \leq 4\} \).
- \(( f+g) ( x) =f( x) +g( x) =\sqrt{x-1}+\sqrt{4-x}\). The domain of \(( f+g) ( x) \) is the closed interval \([ 1,4] \).
- \(( f-g) ( x) =f( x) -g( x) =\sqrt{x-1}-\sqrt{4-x}\). The domain of \(( f-g) ( x) \) is the closed interval \([ 1,4] \).
- \(( f\cdot g) ( x) =f( x) \cdot g( x)\, {=}\,( \sqrt{x-1}) ( \sqrt{4-x} ) =\sqrt{-x^{2}+5x-4}\). The domain of \(( f\cdot g) ( x) \) is the closed interval \([ 1,4] \).
- \(\left( \dfrac{f}{g}\right)\ ( x) =\dfrac{ f( x) }{g( x) }=\dfrac{\sqrt{x-1}}{\sqrt{4-x}}=\dfrac{ \sqrt{-x^{2}+5x-4}}{4-x}\). The domain of \(\left( \dfrac{f}{g}\right) ( x) \) is the half-open interval \([1,4)\).
25
NOW WORK
Problem 11.
2 Form a Composite Function

Suppose an oil tanker is leaking, and your job requires you to find the area of the circular oil spill surrounding the tanker. You determine that the radius of the spill is increasing at a rate of \(3\) meters per minute. That is, the radius \(r\) of the spill is a function of the time \(t\) in minutes since the leak began, and can be written as \(r( t) =3t\).
For example, after \(20\) minutes the radius of the spill is \(r( 20) =3\cdot 20=60\) meters. Recall that the area \(A\) of a circle is a function of its radius \(r\); that is, \(A( r) =\pi r^{2}\). So, the area of the oil spill after \(20\) minutes is \(A( 60) =\pi ( 60^{2}) =3600\pi \) square meters. Notice that the argument \(r\) of the function \(A\) is itself a function, and that the area \(A\) of the oil spill is found at any time \(t\) by evaluating the function \(A=A(r( t)) \).
Functions such as \(A=A(r( t)) \) are called composite functions.
Another example of a composite function is \(y=( 2x+3) ^{2}\). If \( y=f( u) =u^{2}\) and \(u=g( x) =2x+3\), then by substituting \(g( x) =2x+3\) for \(u\), we obtain the original function: \[ \begin{array}{l} y = f(u) = f(g(x)) = (2x + 3)^2 \\ {\color{#0066A7}{\,\,\,\,\,\,\,\,\,\,\,\,u\, = \mathop g\limits^ \uparrow (x)\,\,\,g(x)\mathop = \limits^ \uparrow 2x + 3}} \\ \end{array} \]
This substitution process is called composition.
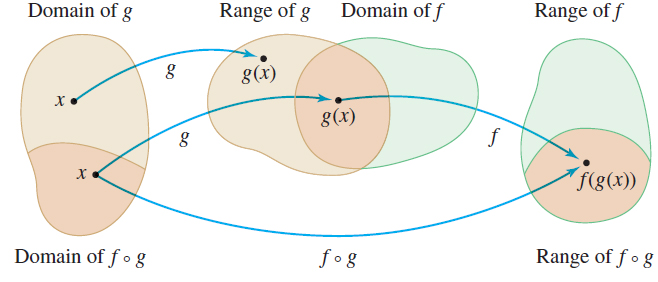
In general, suppose that \(f\) and \(g\) are two functions and that \(x\) is a number in the domain of \(g\). By evaluating \(g\) at \(x\), we obtain \(g( x)\). Now, if \(g( x) \) is in the domain of the function \(f\), we can evaluate \(f\) at \(g( x) ,\) obtaining \(f( g( x) )\). The correspondence from \(x\) to \(f( g( x) )\) is called composition.
spanDEFINITIONspan Composite Function
Given two functions \(f\) and \(g\), the composite function, denoted by \(f\circ g\) (read "\(f\) composed with \(g\)") is defined by \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{(f\, \circ \,g)(x) = f(g(x))}} \]
The domain of \(f\circ g\) is the set of all numbers \(x\) in the domain of \(g\) for which \(g( x) \) is in the domain of \(f\).
Figure 40 illustrates the definition. Only those numbers \(x\) in the domain of \(g\) for which \(g( x) \) is in the domain of \(f\) are in the domain of \(f\circ g\). As a result, the domain of \(f\circ g\) is a subset of the domain of \(g\), and the range of \(f\circ g\) is a subset of the range of \( f \).
26
Evaluating a Composite Function
NOTE
The "inside" function \(g,\) in \( f( g ( x ) ) ,\) is evaluated first.
Suppose that \(f( x) =\dfrac{1}{x+2}\) and \(g( x) =\dfrac{4}{x-1}\).
- \( ( f\circ g ) ( 0 ) =f ( g (0 ) ) =f ( -4 ) =\dfrac{1}{-4+2}=-\dfrac{1}{2} \quad \quad {\color{#0066A7}{{g} ( {x} )}} {\color{#0066A7}{=}} {\color{#0066A7}{\dfrac{4}{x-1}}}{\color{#0066A7}{;\;}} {\color{#0066A7}{{g}}} {\color{#0066A7}{( {0} )}} {\color{#0066A7}{=}}{\color{#0066A7}{-4}}\)
- \( \begin{array}{l} (g \circ f)(1) = g(f(1))\mathop = \limits_ {\color{#0066A7}{\uparrow}} g\left( {\frac{1}{3}} \right) = \frac{4}{{\frac{1}{3} - 1}} = \frac{4}{{ - \frac{2}{3}}} = - 6 \\ {\color{#0066A7}{ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f(x) = \frac{1}{{x + 2}};\,f(1) = \frac{1}{3}}} \\ \end{array} \)
- \( ( f\circ f ) ( 1 ) =f ( f ( 1 ) ) =f \left( \dfrac{1}{3} \right) =\dfrac{1}{\dfrac{1}{3}+2}= \dfrac{1}{\dfrac{7}{3}}=\dfrac{3}{7}\)
- \( \begin{array}{l} (g \circ g)( - 3) = g(g(-3))\mathop = \limits_ {\color{#0066A7}{\uparrow}} g\left( { - 1} \right) = \frac{4}{{ - 1 - 1}} = - 2 \\ {\color{#0066A7}{ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,g(x) = \frac{4}{{x - 1}};\,g( - 3) = \frac{4}{{ - 3 - 1}} = - 1}} \\ \end{array} \)
NOW WORK
Problem 15.
Finding the Domain of a Composite Function
Suppose that \(f( x) =\dfrac{1}{x+2}\) and \(g( x) = \dfrac{4}{x-1}\). Find \(f\circ g\) and its domain.
Solution \[ ( f\circ g) ( x) =f( g( x) ) =\dfrac{1}{g( x) +2}=\dfrac{1}{\dfrac{4}{x-1}+2}= \dfrac{x-1}{4+2( x-1) }=\dfrac{x-1}{2x+2} \]
To find the domain of \(f\circ g,\) first note that the domain of \(g\) is \( \{ x|x\neq 1\} ,\) so we exclude 1 from the domain of \(f\circ g.\) Next note that the domain of \(f\) is \(\{ x|x\neq -2\} \), which means \(g( x) \) cannot equal \(-2.\) To determine what additional values of \(x\) to exclude, we solve the equation \(g( x) =-2\): \[ \begin{array}{l} \frac{4}{{x - 1}} = - 2 \quad \quad {\color{#0066A7}{g(x) = - 2}} \\ \,\, \,\,\,\,\,\,\,4 = - 2(x - 1) \\ \,\,\, \,\,\,\,\,\,4 = - 2x + 2 \\ \,\,\,\,\,\,2x = - 2 \\ \,\,\,\, \,\,\,\,\,x = - 1 \\ \end{array} \]
We also exclude \(-1\) from the domain of \(f\,{\circ}\, g.\)
The domain of \(f\circ g\) is \(\{ x|x\neq -1\), \(x\neq 1\}\).
We could also find the domain of \(f\circ g\) by first finding the domain of \( g\): \(\{ x|x\neq 1\}\). So, exclude \(1\) from the domain of \( f\circ g\). Then looking at \(( f\circ g) ( x) =\dfrac{ x-1}{2x+2}=\dfrac{x-1}{2( x+1) }\), notice that \(x\neq -1\), so we exclude \(-1\) from the domain of \(f\circ g.\) Therefore, the domain of \(f\circ g\) is \(\{ x|x\neq -1\), \(x\neq 1\}\).
NOW WORK
Problem 23.
27
In general, the composition of two functions \(f\) and \(g\) is not commutative. That is, \(f\circ g\) almost never equals \(g\circ f\). For example, in Example 3, \[ ( g\circ f) ( x) =g( f( x) ) = \dfrac{4}{f( x) -1}=\dfrac{4}{\dfrac{1}{x+2}-1}=\dfrac{4( x+2) }{1-( x+2) }=-\dfrac{4( x+2) }{x+1} \]
Functions \(f\) and \(g\) for which \(f\circ g\) \(=g\circ f\) will be discussed in the next section.
Some techniques in calculus require us to "decompose" a composite function. For example, the function \(H( x) =\sqrt{x+1}\) is the composition \( f\circ g\) of the functions \(f( x) =\sqrt{x}\) and \(g( x) =x+1\).

Decomposing a Composite Function
Find functions \(f\) and \(g\) so that \(f\circ g=F\) when:
- \(F( x) =\dfrac{1}{x+1}\)
- \(F( x) =( x^{3}-4x-1) ^{100}\)
- \(F(t) =\sqrt{2-t}\)
Solution (a) If we let \(f( x) =\dfrac{1}{x}\) and \(g( x) =x+1\), then \[ ( f\circ g) ( x) =f( g( x) ) = \dfrac{1}{g( x) }=\dfrac{1}{x+1}=F( x) \]
(b) If we let \(f( x) =x^{100}\) and \(g( x) =x^{3}-4x-1,\) then \[ ( f\circ g) ( x) =f( g( x) ) =f( x^{3}-4x-1) =( x^{3}-4x-1) ^{100}=F( x) \]
(c) If we let \(f( t) =\sqrt{t}\) and \(g( t) =2-t,\) then \[ ( f\circ g) ( t) =f( g( t) ) =f( 2-t) =\sqrt{2-t}=F( t) \]
Although the functions \(f\) and \(g\) chosen in Example 4 are not unique, there is usually a "natural" selection for \(f\) and \(g\) that first comes to mind. When decomposing a composite function, the "natural" selection for \(g\) is often an expression inside parentheses, in a denominator, or under a radical.
NOW WORK
Problem 27.
3 Transform the Graph of a Function with Vertical and Horizontal Shifts
At times we need to graph a function that is very similar to a function with a known graph. Often techniques, called transformations, can be used to draw the new graph.
First we consider translations. Translations shift the graph from one position to another without changing its shape, size, or direction.
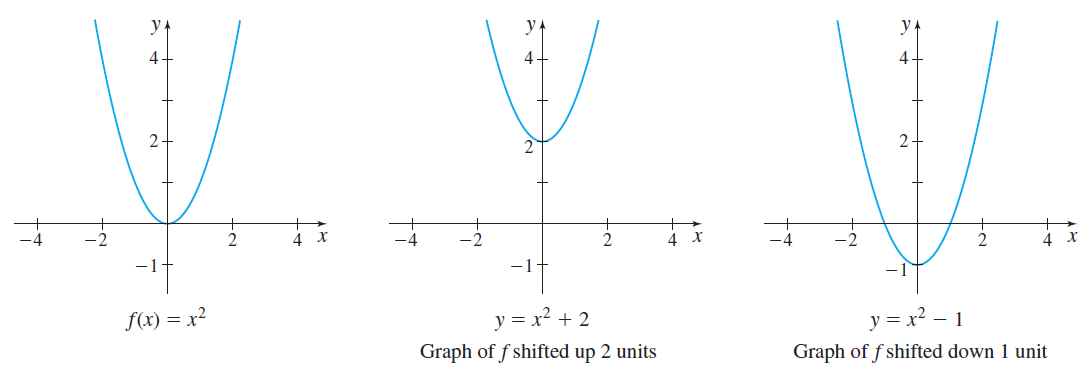
For example, let \(f\) be a function with a known graph, say, \(f( x) =x^{2}\). If \(k\) is a positive number, then adding \(k\) to \(f\) adds \(k\) to each \(y\)-coordinate, causing the graph of \(f\) to shift vertically up \(k\) units. On the other hand, subtracting \(k\) from \(f\) subtracts \(k\) from each \(y\)-coordinate, causing the graph of \(f\) to shift vertically down \(k\) units. See Figure 41 on page 28.
So, adding (or subtracting) a positive constant to a function shifts the graph of the original function vertically up (or down). Now we investigate how to shift the graph of a function right or left.
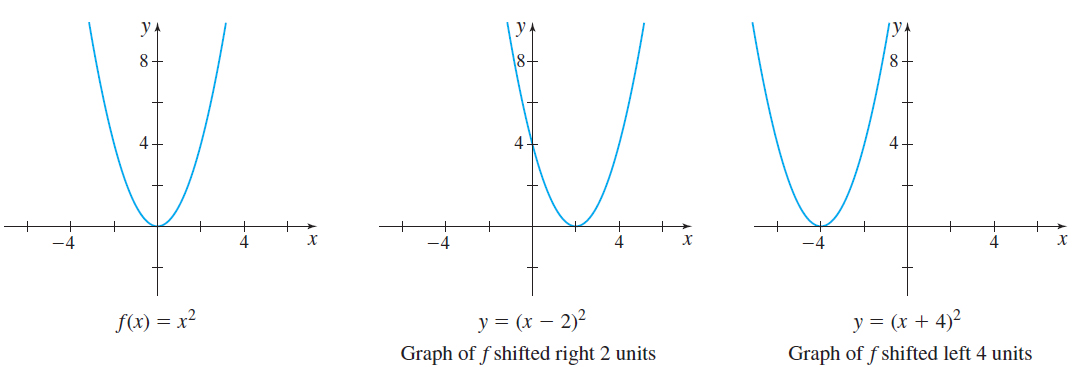
Again, let \(f\) be a function with a known graph, say, \(f( x) =x^{2} \), and let \(h\) be a positive number. To shift the graph to the right \( h\) units, subtract \(h\) from the argument of \(f.\) In other words, replace the argument \(x\) of a function \(f\) by \(x-h\), \(h>0.\) The graph of the new function \(y=f( x-h) \) is the graph of \(f\) shifted horizontally right \(h\) units. On the other hand, if we replace the argument \(x\) of a function \(f\) by \(x+h,\) \(h>0\), the graph of the new function \( y=f( x+h) \) is the graph of \(f\) shifted horizontally left \(h\) units. See Figure 42 on page 28.
28
The graph of a function \(f\) can be moved anywhere in the plane by combining vertical and horizontal shifts.
Combining Vertical and Horizontal Shifts
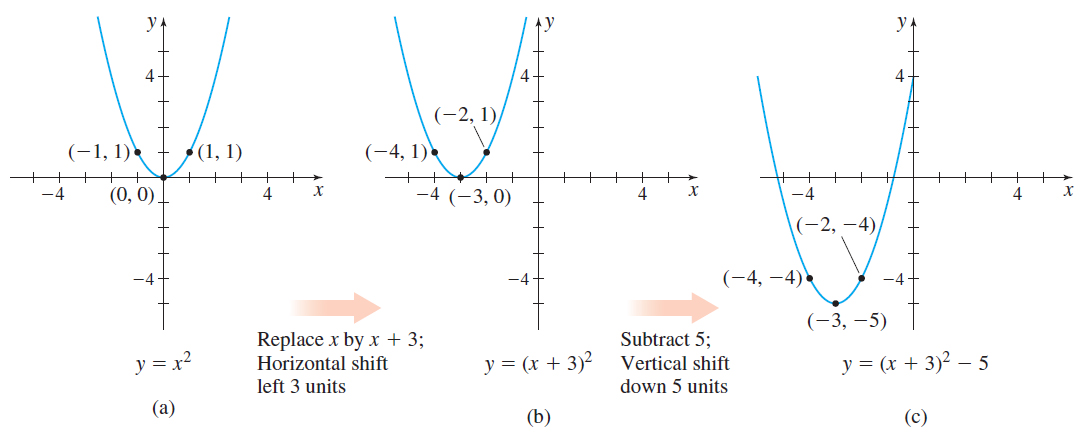
Use transformations to graph the function \(f( x) = ( x+3) ^{2}-5\).
Solution Graph \(f\) in steps:
- Observe that \(f\) is basically a square function, so begin by graphing \( y=x^{2}\) in Figure 43(a).
- Replace the argument \(x\) with \(x+3\) to obtain \(y=( x+3) ^{2}\). This shifts the graph of \(f\) horizontally to the left \(3\) units, as shown in Figure 43(b).
- Finally, subtract \(5\) from each \(y\)-coordinate, which shifts the graph in Figure 43(b) vertically down \(5\) units, and results in the graph of \( f( x) =( x+3) ^{2}-5\) shown in Figure 43(c).
29
Notice the points plotted in Figure 43. Using key points can be helpful in keeping track of the transformation that has taken place.
NOW WORK
Problem 39.
4 Transform the Graph of a Function with Compressions and Stretches
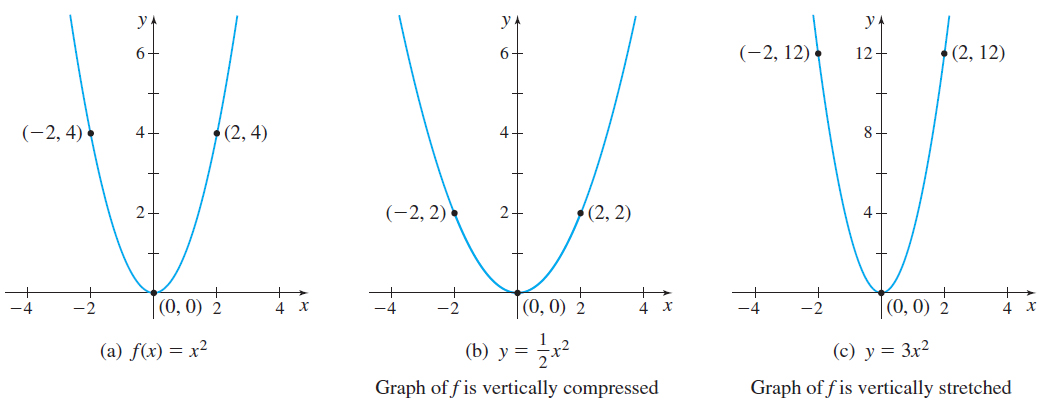
When a function \(f\) is multiplied by a positive number \(a\), the graph of the new function \(y=af( x) \) is obtained by multiplying each \(y\) -coordinate on the graph of \(f\) by \(a\). The new graph is a vertically compressed version of the graph of \(f\) if \( 0<a<1\), and is a vertically stretched version of the graph of \(f\) if \(a>1.\) Compressions and stretches change the proportions of a graph.
For example, the graph of \(f( x) = x^{2}\) is shown in Figure 44(a). Multiplying \(f\) by \(a=\dfrac{1}{2}\) produces a new function \(y=\dfrac{ 1}{2}f( x) =\dfrac{1}{2}x^{2}\), which vertically compresses the graph of \(f\) by a factor of \(\dfrac{1}{2}\), as shown in Figure 44(b). On the other hand, if \(a=3,\) then multiplying \(f\) by \(3\) produces a new function \( y=3~f( x) =3x^{2}\), and the graph of \(f\) is vertically stretched by a factor of 3, as shown in Figure 44(c).
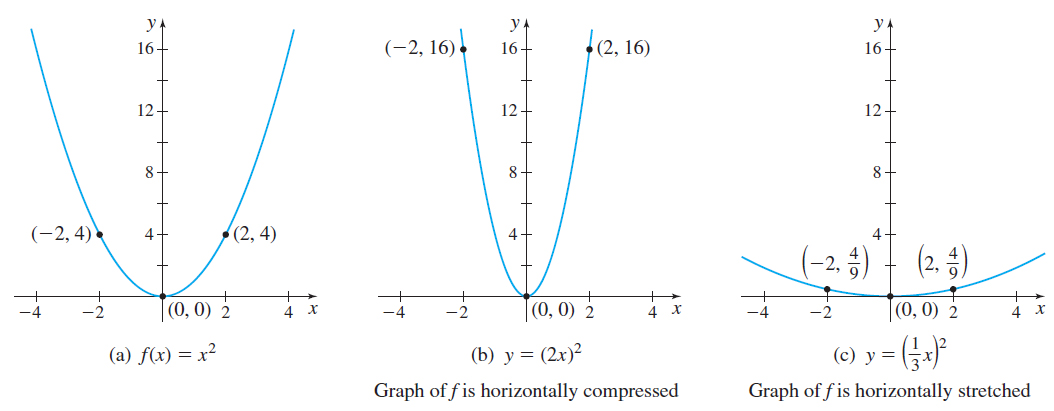
If the argument \(x\) of a function \(f\) is multiplied by a positive number \( a \), the graph of the new function \(y=f( ax) \) is a horizontal compression of the graph of \(f\) when \(a>1\), and a horizontal stretch of the graph of \(f\) when \(0<a<1\).
For example, the graph of \(y=f( 2x) =( 2x) ^{2}=4x^{2}\) is a horizontal compression of the graph of \(f( x) =x^{2}.\) See Figure 45(a) and 45(b). On the other hand, if \(a=\dfrac{1}{3}\), then the graph of \(y=\left( \dfrac{1}{3}x\right) ^{\!\!2}=\dfrac{1}{9}x^{2}\) is a horizontal stretch of the graph of \(f( x) =x^{2}.\) See Figure 45(c).
5 Transform the Graph of a Function by Reflecting It about the x-axis or the y-axis
30
The third type of transformation, reflection about the \(x\)- or \(y\)-axis, changes the orientation of the graph of the function \(f\) but keeps the shape and the size of the graph intact.
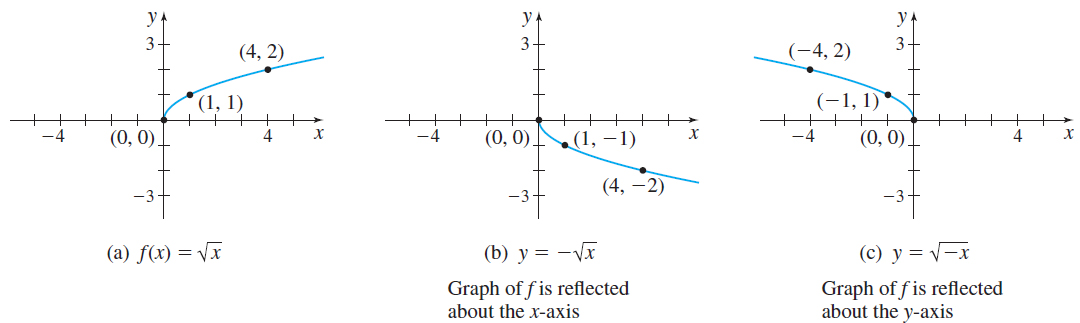
When a function \(f\) is multiplied by \(-1,\) the graph of the new function \( y=-f( x) \) is the reflection about the \(x\)-axis of the graph of \(f\). For example, if \(f( x) =\sqrt{x}\), then the graph of the new function \(y=-f( x) =-\sqrt{x}\) is the reflection of the graph of \(f\) about the \(x\)-axis. See Figures 46(a) and 46(b).
If the argument \(x\) of a function \(f\) is multiplied by \(-1\), then the graph of the new function \(y=f( -x) \) is the reflection about the \(y\)-axis of the graph of \(f\). For example, if \(f( x) =\sqrt{x}\), then the graph of the new function \(y=f( -x) \) \(=\sqrt{-x}\) is the reflection of the graph of \(f\) about the \(y\)-axis. See Figures 46(a) and 46(c). Notice in this example that the domain of \(y=\sqrt{-x}\) is all real numbers for which \(-x\geq 0\), or equivalently, \(x\leq 0.\)
Combining Transformations
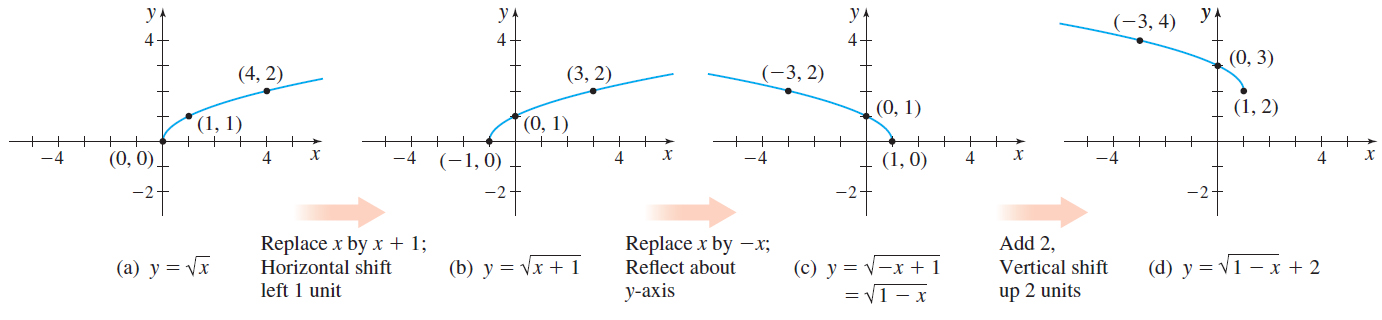
Use transformations to graph the function \(f( x) =\sqrt{1-x}+2\).
Solution We graph \(f\) in steps:
- Observe that \(f\) is basically a square root function, so we begin by graphing \(y=\sqrt{x}\). See Figure 47(a).
- Now we replace the argument \(x\) with \(x+1\) to obtain \(y=\sqrt{x+1},\) which shifts the graph of \(y=\sqrt{x}\) horizontally to the left \(1\) unit, as shown in Figure 47(b).
- Then we replace \(x\) with \(-x\) to obtain \(y=\sqrt{-x+1}=\sqrt{1-x},\) which reflects the graph about the \(y\)-axis. See Figure 47(c).
- Finally, we add \(2\) to each \(y\)-coordinate, which shifts the graph vertically up 2 units, and results in the graph of \(f( x) = \sqrt{1-x}+2\) shown in Figure 47(d).
NOW WORK
Problem 43.