P.3 Assess Your UnderstandingPrinted Page 31
31
Concepts and Vocabulary
If the domain of a function \(f\) is \(\{ x|0\leq x\leq 7\} \) and the domain of a function \(g\) is \(\{ x|{-}2\leq x\leq 5\} ,\) then the domain of the sum function \(f+g\) is _____.
\(\{x | 0 \le x \le 5\}\)
True or False \(\quad\) If \(f\) and \(g\) are functions, then the domain of \(\dfrac{f}{g}\) consists of all numbers \(x\) that are in the domains of both \(f\) and \(g\).
False
True or False \(\quad\) The domain of \( f\cdot g \) consists of the numbers \(x\) that are in the domains of both \(f\) and \(g\).
True
True or False \(\quad\) The domain of the composite function \( f\circ g\) is the same as the domain of \(g( x) \).
False
True or False \(\quad\) The graph of \(y=-f( x)\) is the reflection of the graph of \(y=f( x) \) about the \(x\)-axis.
True
True or False \(\quad\) To obtain the graph of \(y=f(x+2) -3\), shift the graph of \(y=f( x) \) horizontally to the right 2 units and vertically down 3 units.
False
True or False \(\quad\) Suppose the \(x\)-intercepts of the graph of the function \(f\) are \(-3\) and \(2\). Then the \(x\)-intercepts of the graph of the function \(y=2f( x) \) are \(-3\) and \(2.\)
True
Suppose that the graph of a function \(f\) is known. Then the graph of the function \(y=f( x-2) \) can be obtained by a(n)_____ shift of the graph of \(f\) to the _____ a distance of 2 units.
Horizontal, right
Suppose that the graph of a function \(f\) is known. Then the graph of the function \(y=f( -x) \) can be obtained by a reflection about the _____-axis of the graph of \(f\).
\(y\)
Suppose the \(x\)-intercepts of the graph of the function \(f\) are \(-2\), \(1\), and \(5\). The \(x\)-intercepts of \(y=f( x+3) \) are _____, _____, and _____.
\(-5\), \(-2\), \(2\)
Practice Problems
In Problems 11–14, the functions \(f\) and \(g\) are given. Find each of the following functions and determine their domain:
- (a) \(( f+g) ( x) \)
- (b) \((f-g) ( x) \)
- (c) \(( f\cdot g) ( x) \)
- (d) \(\left( \dfrac{f}{g}\right) ( x)\)
\(f( x) =3x+4\) and \(g( x) =2x-3\)
- (a) \((f+g)(x)=5x+1\), domain: \((-\infty, \infty)\)
- (b) \((f-g)(x)=x+7\), domain: \((-\infty, \infty)\)
- (c) \((f\cdot g)(x)=6x^2-x-12\), domain: \((-\infty, \infty)\)
- (d) \(\left(\frac{f}{g}\right)(x)=\frac{3x+4}{2x-3}\), domain: \(\left\{ x | x \neq \frac{3}{2}\right\}\)
\(f( x) =1+\dfrac{1}{x}\) and \(g( x) =\dfrac{1}{x}\)
\(f( x) =\sqrt{x+1}\) and \(g( x) =\dfrac{2}{x}\)
- (a) \((f+g)(x)=\sqrt{x+1}+ \frac{2}{x}\), domain:\(\{ x | -1 \le x < 0\}\cup \{x | x > 0\}\)
- (b) \((f-g)(x)=\sqrt{x+1}- \frac{2}{x}\), domain: \(\{ x | -1 \le x < 0\}\cup \{x | x > 0\}\)
- (c) \((f\cdot g)(x)=\frac{2\sqrt{x+1}}{x}\), domain: \(\{ x | -1 \le x < 0\}\cup \{x | x > 0\}\)
- (d) \(\left(\frac{f}{g}\right)(x)=\frac{1}{2}x\sqrt{x+1}\), domain: \(\{ x | x \ge -1,x\neq 0\}\)
\(f( x) =\vert x\vert \) and \(g( x) =x\)
In Problems 15 and 16, for each of the functions \(f\) and \(g\), find:
- (a) \(( f\circ g) ( 4)\)
- (b) \(( g\circ f) ( 2)\)
- (c) \(( f\circ f) ( 1)\)
- (d) \(( g\circ g) ( 0)\)
\(f( x) =2x\) and \(g( x) =3x^{2}+1\)
- (a) \((f\circ g)(4)=98\)
- (b) \((g\circ f)(2)=49\)
- (c) \((f\circ f)(1)=4\)
- (d) \((g\circ g)(0)=4\)
\(f( x) =\dfrac{3}{x+1}\) and \(g( x) =\sqrt{x}\)
In Problems 17 and 18, evaluate each expression using the values given in the table.
\(x\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\) \(f( x) \) \(-7\) \(-5\) \(-3\) \(-1\) \(3\) \(5\) \(7\) \(g( x)\) \(8\) \(3\) \(0\) \(-1\) \(0\) \(3\) \(8\) - (a) \(( f\circ g) ( 1) \)
- (b) \(( f\circ g) ( -1) \)
- (c) \(( g\circ f) ( -1) \)
- (d) \(( g\circ f) ( 1) \)
- (e) \(( g\circ g) ( -2) \)
- (f) \(( f\circ f) ( -1) \)
- (a) \((f\circ g)(1)=-1\)
- (b) \((f\circ g)(-1)=-1\)
- (c) \((g\circ f)(-1) = 8\)
- (d) \((g\circ f)(1)=8\)
- (e) \((g\circ g)(-2)=8\)
- (f) \((f\circ f)(-1) = -7\)
\(x\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\) \(f( x)\) \(11\) \(9\) \(7\) \(5\) \(3\) \(1\) \(-1\) \(g( x)\) \(-8\) \(-3\) \(0\) \(1\) \(0\) \(-3\) \(-8\) - (a) \(( f\circ g) ( 1) \)
- (b) \(( f\circ g) ( 2) \)
- (c) \(( g\circ f) ( 2) \)
- (d) \(( g\circ f) ( 3) \)
- (e) \(( g\circ g) ( 1) \)
- (f) \(( f\circ f) ( 3) \)
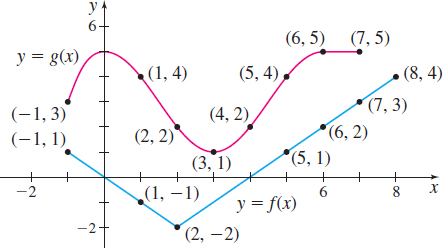
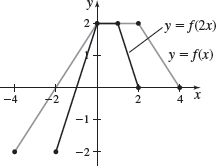
In Problems 19 and 20, evaluate each composite function using the graphs of \(y=f( x) \) and \(y=g( x) \) shown in the figure below.
- (a) \(( g\circ f) ( -1) \)
- (b) \(( g\circ f) ( 6) \)
- (c) \(( f\circ g) ( 6) \)
- (d) \(( f\circ g) ( 4) \)
- (a) \((g\circ f)(-1)=4\)
- (b) \((g\circ f)(6)=2\)
- (c) \((f\circ g)(6)=1\)
- (d) \((f\circ g)(4)=-2\)
- (a) \(( g\circ f) ( 1) \)
- (b) \(( g\circ f) ( 5) \)
- (c) \(( f\circ g) ( 7) \)
- (d) \(( f\circ g) ( 2) \)
In Problems 21–26, for the given functions \(f\) and \(g\), find:
- (a) \(f\circ g\)
- (b) \(g\circ f\)
- (c) \(f\circ f\)
- (d) \(g\circ g\)
State the domain of each composite function.
\(f( x) =3x+1\) and \(g( x) =8x\)
- (a) \((f\circ g)(x)=24x+1\), domain: \((-\infty, \infty)\)
- (b) \((g\circ f)(x)=24x+8\), domain: \((-\infty, \infty)\)
- (c) \((f\circ f)(x)=9x+4\), domain: \((-\infty, \infty)\)
- (d) \((g\circ g)(x)=64x\), domain: \((-\infty, \infty)\)
\(f( x) =-x\) and \(g( x) =2x-4\)
\(f( x) =x^{2}+1\) and \(g( x) =\sqrt{x-1}\)
- (a) \((f\circ g)(x)=x\), domain: \(\{ x | x \ge 1\}\)
- (b) \((g\circ f)(x)=|x|\), domain: \((-\infty, \infty)\)
- (c) \((f\circ f)(x)=x^4+2x^2+2\), domain: \((-\infty, \infty)\)
- (d) \((g\circ g)(x)=\sqrt{\sqrt{x-1}-1}\), domain: \(\{ x | x \ge 2\}\)
\(f( x) =2x+3\) and \(g( x) =\sqrt{x}\)
\(f( x) =\dfrac{x}{x-1}\) and \(g( x) = \dfrac{2}{x}\)
- (a) \((f\circ g)(x)=\frac{2}{2-x}\), domain: \(\{ x | x \neq 0, x \neq 2\}\)
- (b) \((g\circ f)(x)=\frac{2(x-1)}{x}\), domain: \(\{ x | x \neq 0, x \neq 1\}\)
- (c) \((f\circ f)(x)=x\), domain: \(\{ x | x \neq 1\}\)
- (d) \((g\circ g)(x)=x\), domain: \(\{ x | x \neq 0\}\)
\(f( x) =\dfrac{1}{x+3}\) and \(g( x) =-\dfrac{2}{x}\)
In Problems 27–32, find functions \(f\) and \(g\) so that \(f\circ g=F\).
\(F( x) = ( 2x+3) ^{4}\)
\(f(x) = x^4\), \(g(x) = 2x+3\)
\(F( x) = ( 1+x^{2}) ^{3}\)
\(F( x) =\sqrt{x^{2}+1}\)
\(f(x) = \sqrt{x}\), \(g(x) = x^2+1\)
\(F( x) =\sqrt{1-x^{2}}\)
\(F( x) = \vert 2x+1\vert \)
\(f(x) = |x|\), \(g(x) = 2x+1\)
\(F( x) = \vert 2x^{2}+3\vert\)
32
In Problems 33–46, graph each function using the graphing techniques of shifting, compressing, stretching, and/or reflecting. Begin with the graph of a basic function and show all stages.
\(f( x) =x^{3}+2\)
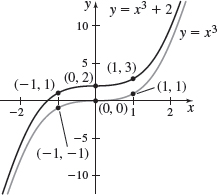
\(g( x) =x^{3}-1\)
\(h( x) =\sqrt{x-2}\)
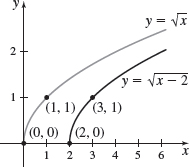
\(f( x) =\sqrt{x+1}\)
\(g( x) =4\sqrt{x}\)
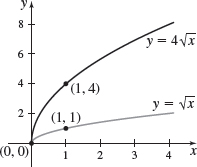
\(f( x) =\dfrac{1}{2}\sqrt{x}\)
\(f( x) =( x-1) ^{3}+2\)

\(g( x) =3( x-2) ^{2}+1\)
\(h( x) =\dfrac{1}{2x}\)
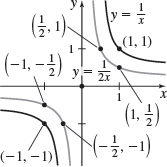
\(f( x) =\dfrac{4}{x}+2\)
\(G( x) =2 \vert 1-x\vert \)

\(g( x) =-( x+1) ^{3}-1\)
\(g( x) =-4\sqrt{x-1}\)
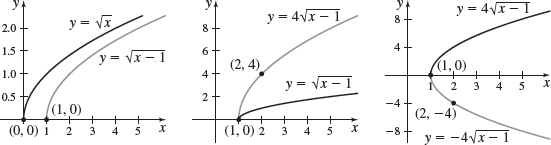
\(f( x) =4\sqrt{2-x}\)
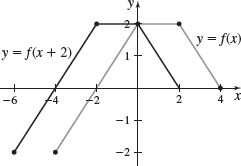
In Problems 47 and 48, the graph of a function \(f\) is illustrated. Use the graph of \(f\) as the first step in graphing each of the following functions:
- (a) \(F( x) =f( x) +3\)
- (b) \(G( x) =f( x+2) \)
- (c) \(P( x) =-f( x) \)
- (d) \(H( x) =f( x+1) -2\)
- (e) \(Q( x) =\dfrac{1}{2}f( x) \)
- (f) \(g( x) =f( -x) \)
- (g) \(h( x) =f( 2x)\)
- (a)
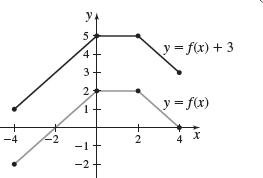
- (b)
- (c)
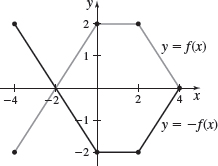
- (d)
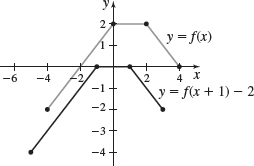
- (e)
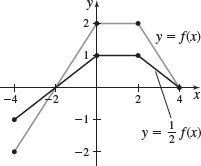
- (f)
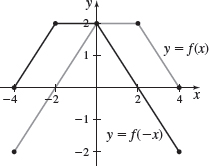
- (g)
 Period of a Pendulum \(\quad\) The period \(T\) (in seconds) of a simple pendulum is a function of its length \(l\) (in meters) defined by the equation \[ T=2\pi \sqrt{\dfrac{l}{g}} \] where \(g\approx 9.8\) meters / second\(^{2}\) is the acceleration due to gravity.
Period of a Pendulum \(\quad\) The period \(T\) (in seconds) of a simple pendulum is a function of its length \(l\) (in meters) defined by the equation \[ T=2\pi \sqrt{\dfrac{l}{g}} \] where \(g\approx 9.8\) meters / second\(^{2}\) is the acceleration due to gravity.- (a) Use a graphing utility to graph the function \(T=T ( l).\)
- (b) Now graph the functions \(T=T ( l+1) ,\) \(T=T ( l+2) ,\) and \(T=T ( l+3) \).
- (c) Discuss how adding to the length \(l\) changes the period \(T\).
- (d) Now graph the functions \(T=T ( 2l) ,\) \(T=T ( 3l) ,\) and \(T=T ( 4l) \).
- (e) Discuss how multiplying the length \(l\) by 2, 3, and 4 changes the period \(T\).
- (a)

- (b)
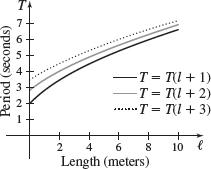
- (c) Answers will vary.
- (d)
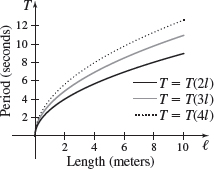
- (e) Answers will vary.
Suppose \(( 1,3) \) is a point on the graph of \(y=g( x) \).
- (a) What point is on the graph of \(y=g( x+3) -5?\)
- (b) What point is on the graph of \(y=-2g( x-2) +1?\)
- (c) What point is on the graph of \(y=g( 2x+3) ?\)


