P.4 Inverse Functions
OBJECTIVES
When you finish this section, you should be able to:
- Determine whether a function is one-to-one (p. 32)
- Determine the inverse of a function defined by a set of ordered pairs (p. 34)
- Obtain the graph of the inverse function from the graph of a one-to-one function (p. 35)
- Find the inverse of a one-to-one function defined by an equation (p. 35)
1 Determine Whether a Function Is One-to-One
By definition, for a function \(y = f(x)\), if \(x\) is in the domain of \(f\), then \(x\) has one, and only one, image \(y\) in the range. If a function \(f\) also has the property that no \(y\) in the range of \(f\) is the image of more than one \(x\) in the domain, then the function is called a one-to-one function.
spanDEFINITIONspan One-to-One Function
A function \(f\) is a one-to-one function if any two different inputs in the domain correspond to two different outputs in the range. That is, if \(x_{1} \neq x_2\), then \(f (x_{1}) \neq f (x_{2})\).
33
IN WORDS
A function is not one-to-one if there are two different inputs in the domain corresponding to the same output.
Figure 48 illustrates the distinction among one-to-one functions, functions that are not one-to-one, and relations that are not functions.
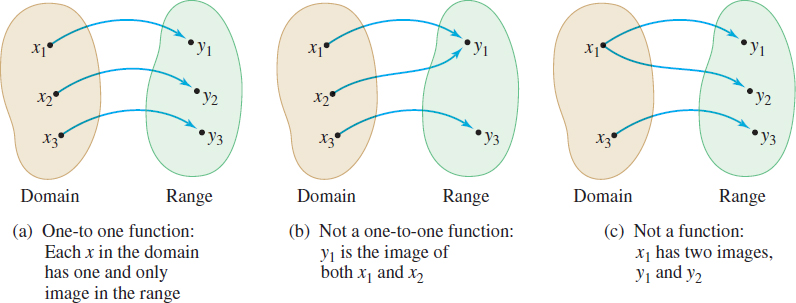
If the graph of a function \(f\) is known, there is a simple test called the Horizontal-line Test, to determine whether \(f\) is a one-to-one function.
THEOREM Horizontal-line Test
The graph of a function in the \(xy\)-plane is the graph of a one-to-one function if and only if every horizontal line intersects the graph in at most one point.
Determining Whether a Function Is One-to-One
Determine whether each of these functions is one-to-one:
- \(f(x) = x^{2}\)
- \(g(x) = x^{3}\)
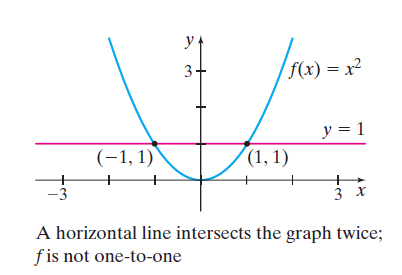
Solution (a) Figure 49 illustrates the Horizontal-line Test for the graph of \(f(x) = x^{2}\). The horizontal line \(y = 1\) intersects the graph of \(f\) twice, at \((1, 1)\) and at \((-1, 1)\), so \(f\) is not one-to-one.
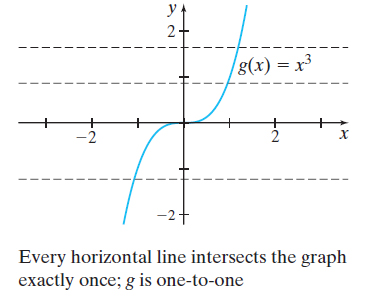
(b) Figure 50 illustrates the horizontal-line test for the graph of \(g(x) = x^{3}\). Because every horizontal line intersects the graph of \(g\) exactly once, it follows that \(g\) is one-to-one.
NOW WORK
Problem 9.
Notice that the one-to-one function \(g(x) = x^{3}\) also is an increasing function on its domain. Because an increasing (or decreasing) function will always have different \(y\)-values for different \(x\)-values, a function that is increasing (or decreasing) on an interval is also a one-to-one function on that interval.
34
THEOREM One-to-One Function
- A function that is increasing on an interval \(I\) is a one-to-one function on \(I\).
- A function that is decreasing on an interval \(I\) is a one-to-one function on \(I\).
2 Determine the Inverse of a Function Defined by a Set of Ordered Pairs
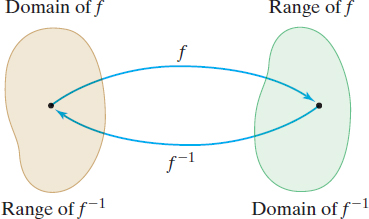
Suppose that \(f\) is a one-to-one function. Then to each \(x\) in the domain of \(f\), there is exactly one image \(y\) in the range (because \(f\) is a function); and to each \(y\) in the range of \(f\), there is exactly one \(x\) in the domain (because \(f\) is one-to-one). The correspondence from the range of \(f\) back to the domain of \(f\) is also a function, called the inverse function of \(f\). The symbol \(f^{-1}\) is used to denote the inverse of \(f\).
NOTE
\({f}^{-1}\) is not the reciprocal function. That is, \(f^{-1} (x) \neq \dfrac{1}{f(x)}\). The reciprocal function \(\dfrac{1}{f(x)}\) is written \([f(x)]^{-1}\).
spanDEFINITIONspan Inverse Function
Let \(f\) be a one-to-one function. The inverse of \(f\), denoted by \(f^{-1}\), is the function defined on the range of \(f\) for which \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{x = f^{ - 1} (y)\quad {\rm{if}}\;{\rm{and}}\;{\rm{only}}\;{\rm{if}}\quad y = f{\rm{(}}x{\rm{)}}}} \]
We will discuss how to find inverses for three representations of functions: (1) sets of ordered pairs, (2) graphs, and (3) equations. We begin with finding the inverse of a function represented by a set of ordered pairs.
If the function \(f\) is a set of ordered pairs \((x, y)\), then the inverse of \(f\), denoted \(f^{\,-1}\), is the set of ordered pairs \((y,x)\).
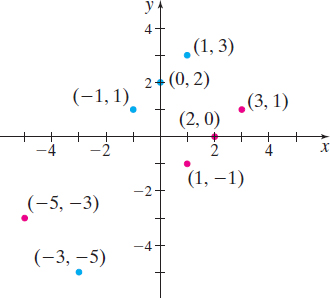
Finding the Inverse of a Function Defined by a Set of Ordered Pairs
Find the inverse of the one-to-one function: \[ \{(-3,-5), (-1,1), (0,2), (1,3)\} \]
State the domain and the range of the function and its inverse.
Solution The inverse of the function is found by interchanging the entries in each ordered pair. The inverse is \[ \{(-5,-3), (1,-1), (2,0), ( 3,1)\} \]
The domain of the function is \(\{-3, -1,0, 1\}\); the range of the function is \(\{-5, 1,2,3\}\). The domain of the inverse function is \(\{-5, 1,2,3\}\); the range of the inverse function is \(\{ -3, -1,0,1\}\).
Figure 51 shows the one-to-one function (in blue) and its inverse (in red).
NOW WORK
Problem 19.
Remember, if \(f\) is a one-to-one function, it has an inverse \(f^{-1}\). See Figure 52. Based on the results of Example 2 and Figure 51, two properties of a one-to-one function \(f\) and its inverse function \(f^{-1}\) become apparent: \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{{\rm{Domain}}\;{\rm{of}}\;f\; = \;{\rm{Range\;of}}\;f^{ - 1} \quad {\rm{Range}}\;{\rm{of}}\;f\; = \;{\rm{Domain}}\;{\rm{of}}\;f^{ - 1}}} \]
The next theorem provides a means for verifying that two functions are inverses of one another.
THEOREM
Given a one-to-one function \(f\) and its inverse function \(f^{-1}\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\begin{array}{*{20}c} { \bullet \;(f^{ - 1} \circ \;f)(x)\; = \;f^{ - 1} (f(x))\; = \;x} & {{\rm{where}}\;x\;{\rm{is}}\;{\mathop{\rm in}\nolimits} \;{\rm{the}}\;{\rm{domain}}\;{\rm{of}}\;f}\\ { \bullet \;(f \circ \;f^{ - 1} )(x)\; = \;f(f^{ - 1} (x))\; = \;x} & \;\;\;{{\rm{where}}\;x\;{\rm{is}}\;{\mathop{\rm in}\nolimits} \;{\rm{the}}\;{\rm{domain}}\;{\rm{of}}\;f^{ - 1} } \\ \end{array}}} \]
35
Verifying Inverse Functions
Verify that the inverse of \(f(x) = \dfrac{1}{x-1}\) is \(f^{-1}(x) = \dfrac{1}{x}+1\). For what values of \(x\) is \(f^{-1} (f( x)) = x?\) For what values of \(x\) is \(f (f^{-1}(x)) = x?\)
Solution The domain of \(f\) is \(\{x|x\neq 1\}\) and the domain of \(f^{\,-1}\) is \(\{ x|x\neq 0\}\). Now \[ \begin{array}{*{20}c} \;\;\;\;\;\;\;\;\;\;{f^{ - 1} (f(x)) = f^{ - 1} \left( {\frac{1}{{x - 1}}} \right) = \frac{1}{{\left( {\frac{1}{{x - 1}}} \right)}} + 1 = x - 1 + 1 = x,} & {{\rm{provided }}\;\;x \ne \;1} \\ {f(f^{ - 1} (x)) = f\left( {\frac{1}{x} + 1} \right) = \frac{1}{{\left( {\frac{1}{x} + 1} \right) - 1}} = \frac{1}{{\frac{1}{x}}} = x,} & {{\rm{provided}}\;x\; \ne 0} \\ \end{array} \]
NOW WORK
Problem 15.
3 Obtain the Graph of the Inverse Function from the Graph of a One-to-One Function
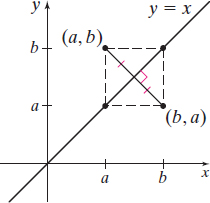
Suppose \((a,b)\) is a point on the graph of a one-to-one function \(f\) defined by \(y = f(x)\). Then \(b = f(a)\). This means that \(a = f^{-1}(b)\), so \((b,a)\) is a point on the graph of the inverse function \(f^{-1}\). Figure 53 shows the relationship between the point \((a,b)\) on the graph of \(f\) and the point \((b,a)\) on the graph of \(f^{-1}\). The line segment containing \((a,b)\) and \((b,a)\) is perpendicular to the line \(y = x\) and is bisected by the line \(y = x\). (Do you see why?) The point \((b,a)\) on the graph of \(f^{\,-1}\) is the reflection about the line \(y=x\) of the point \((a,b)\) on the graph of \(f\).
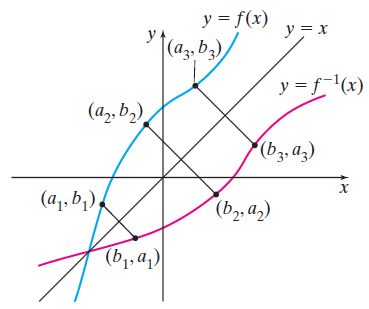
THEOREM Symmetry of Inverse Functions
The graph of a one-to-one function \(f\) and the graph of its inverse function \(f^{-1}\) are symmetric with respect to the line \(y = x\).
We can use this result to find the graph of \(f^{-1}\) given the graph of \(f\). If we know the graph of \(f\), then the graph of \(f^{-1}\) is obtained by reflecting the graph of \(f\) about the line \(y = x\). See Figure 54.
Graphing the Inverse Function from the Graph of a Function
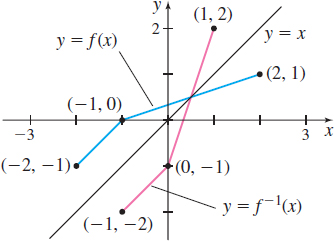
The graph in Figure 55 is that of a one-to-one function \(y = f(x)\). Draw the graph of its inverse function.
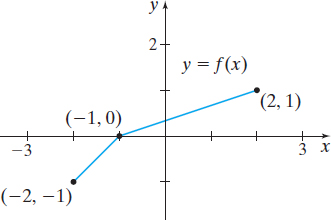
Solution Since the points \((-2,-1)\), \((-1,0)\), and \(( 2,1)\) are on the graph of \(f\), the points \((-1,-2)\), \(( 0,-1)\), and \(( 1,2)\) are on the graph of \(f^{\,-1}\). Using the points and the fact that the graph of \(f^{-1}\) is the reflection about the line \(y = x\) of the graph of \(f\), draw the graph of \(f^{-1}\), as shown in Figure 56.
NOW WORK
Problem 27.
4 Find the Inverse of a One-to-One Function Defined by an Equation
Since the graphs of a one-to-one function \(f\) and its inverse function \(f^{-1}\) are symmetric with respect to the line \(y = x\), the inverse function \(f^{-1}\) can be obtained by interchanging the roles of \(x\) and \(y\) in \(f\). If \(f\) is defined by the equation \[ y = f(x) \]
36
then \(f^{-1}\) is defined by the equation \[ x = f(y)\quad \quad {\color{#0066A7}{{\rm{Interchange}}\;x\;{\rm{and}}\;y}} \]
The equation \(x = f (y)\) defines \(f^{-1}\) implicitly. If the implicit equation can be solved for \(y\), we will have the explicit form of \(f^{-1}\), that is, \[ y = f^{-1}(x) \]
Steps for Finding the Inverse of a One-to-One Function
- Step 1 Write \(f\) in the form \(y = f(x)\).
- Step 2 Interchange the variables \(x\) and \(y\) to obtain \(x = f(y)\) This equation defines the inverse function \(f^{-1}\) implicitly.
- Step 3 If possible, solve the implicit equation for \(y\) in terms of \(x\) to obtain the explicit form of \(f^{-1}\): \(y = f^{-1}( x)\).
- Step 4 Check the result by showing that \(f^{-1} (f(x)) = x\) and \(f( f^{-1}(x)) = x\).

Finding the Inverse Function
The function \(f(x) = 2x^{3}-1\) is one-to-one. Find its inverse.
Solution We follow the steps given above.
Step 1 Write \(f\) as \(y = 2x^{3}-1\).
Step 2 Interchange the variables \(x\) and \(y\). \[ \ x = 2y^{3}-1 \]
This equation defines \(f^{-1}\) implicitly.
Step 3 Solve the implicit form of the inverse function for \(y\). \begin{eqnarray*} x+1 &=&2y^{3} \\[5pt] y^{3} &=&\dfrac{x+1}{2} \\[5pt] y &=&\sqrt[3]{\dfrac{x+1}{2}}=f^{-1}( x) \end{eqnarray*}
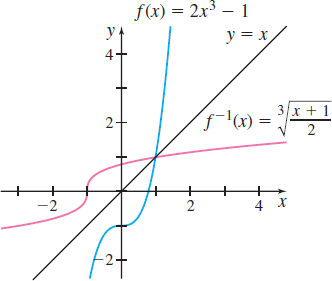
Step 4 Check the result. \[ \begin{array}{c} \;\;\;\;\;\;\;\;\;\;f^{ - 1} (f(x)) = f^{ - 1} (2x^3 - 1) = \sqrt[3]{{\frac{{(2x^3 - 1) + 1}}{2}}} = \sqrt[3]{{\frac{{2x^3 }}{2}}} = \sqrt[3]{{x^3 }} = x \\ f(f^{ - 1} (x)) = f\left( {\sqrt[3]{{\frac{{x + 1}}{2}}}} \right) = 2\left( {\sqrt[3]{{\frac{{x + 1}}{2}}}} \right)^3 - 1 = 2\left( {\frac{{x + 1}}{2}} \right) - 1 \\ \;\;\;\;\;\;\;\;\;= x + 1 - 1 = x \\ \end{array} \]
See Figure 57 for the graphs of \(f\) and \(f^{-1}\).
NOW WORK
Problem 31.
If a function \(f\) is not one-to-one, it has no inverse function. But sometimes we can restrict the domain of such a function so that it is a one-to-one function. Then on the restricted domain the new function has an inverse function.
37
Finding the Inverse of a Domain-Restricted Function
Find the inverse of \(f(x) = x^{2}\) if \(x\geq 0\).
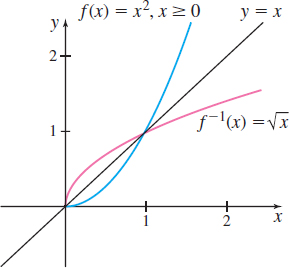
Solution The function \(f(x) = x^{2}\) is not one-to-one (see Example 1(a)). However, by restricting the domain of \(f\) to \(x\geq 0\), the new function \(f\) is one-to-one, so \(f^{-1}\) exists. To find \(f^{-1}\), follow the steps.
- Step 1 \(y=x^{2}\), where \(x\geq 0\).
- Step 2 Interchange the variables \(x\) and \(y\): \(x = y^{2}\), where \(y\geq 0\). This is the inverse function written implicitly.
- Step 3 Solve for \(y\): \(y=\sqrt{x}=f^{-1}(x)\). (Since \(y\geq 0\), only the principal square root is obtained.)
- Step 4 Check that \(f^{-1}(x) = \sqrt{x}\) is the inverse function of \(f\). \[ \begin{array}{rcl@{\qquad}l} f^{-1}( f( x))~&=&\sqrt{f( x) }=\sqrt{x^{2}}=\vert x\vert =x, & \hbox{where }x\geq 0 \\[2pt] f( f^{-1}( x))~&=&[ f^{-1}( x) ] ^{2}=[ \sqrt{x}] ^{2}=x, & \hbox{where }x\geq 0 \end{array} \]
NEED TO REVIEW?
Principal roots are discussed in Appendix A.1, p. A-9.
The graphs of \(f(x) = x^{2},\) \(x\geq 0,\) and \(f^{-1}(x) = \sqrt{x}\) are shown in Figure 58.
NOW WORK
Problem 37.