P.4 Assess Your Understanding
Concepts and Vocabulary
Question
True or False If every vertical line intersects the graph of a function \(f\) at no more than one point, \(f\) is a one-to-one function.
Question
If the domain of a one-to-one function \(f\) is \([4,\infty)\), the range of its inverse function \(f^{-1}\) is _____.
Question
True or False If \(f\) and \(g\) are inverse functions, the domain of \(f\) is the same as the domain of \(g\).
Question
True or False If \(f\) and \(g\) are inverse functions, their graphs are symmetric with respect to the line \(y = x\).
Question
True or False If \(f\) and \(g\) are inverse functions, then \((f \circ g) (x) = f(x) \,\cdot\, g(x)\).
Question
True or False If a function \(f\) is one-to-one, then \(f (f^{-1}( x)) = x\), where \(x\) is in the domain of \(f\).
Question
Given a collection of points \((x,y)\), explain how you would determine if it represents a one-to-one function \(y = f(x)\).
Question
Given the graph of a one-to-one function \(y = f(x)\), explain how you would graph the inverse function \(f^{-1}\).
Practice Problems
In Problems 9–14, the graph of a function f is given. Use the Horizontal-line Test to determine whether f is one-to one.
Question
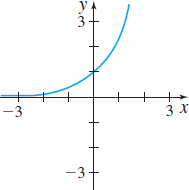
Question
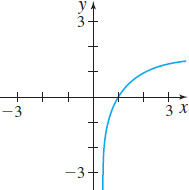
Question
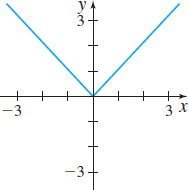
Question
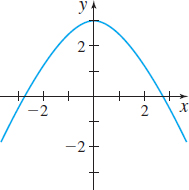
Question

Question
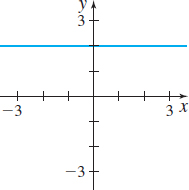
In Problems 15–18, verify that the functions f and g are inverses of each other by showing that \((f\circ g)(x) = x\) and \((g\circ f)(x) = x\).
Question
\(f( x) =3x+4\); \(g( x) = \dfrac{1}{3}( x-4)\)
Question
\(f( x) = x^{3}-8\); \(g(x) = \sqrt[3]{x+8}\)
Question
\(f(x) = \dfrac{1}{x}\); \(g(x) = \dfrac{1}{x}\)
Question
\(f(x) = \dfrac{2x+3}{x+4}\); \(g(x) = \dfrac{4x-3}{2-x}\)
In Problems 19–22, (a) determine whether the function is one-to-one. If it is one-to-one, (b) find the inverse of each one-to-one function. (c) State the domain and the range of the function and its inverse.
Question
\(\{(-3,5), (-2,9), (-1,2), (0,11), ( 1,-5)\}\)
Question
\(\{(-2,2), (-1,6), ( 0,8), ( 1,-3), ( 2,8)\}\)
Question
\(\{(-2,1), (-3,2), (-10,0), (1,9), ( 2,1)\}\)
Question
\(\{(-2,-8), (-1,-1), (0,0), (1,1), (2,8)\}\)
In Problems 23–28, the graph of a one-to-one function f is given. Draw the graph of the inverse function. For convenience, the graph of \(y=x\) is also given.
Question
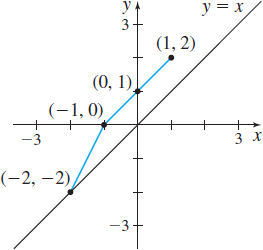
Question
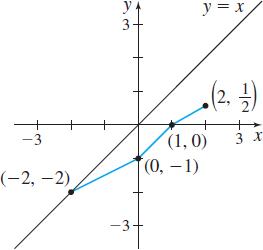
Question
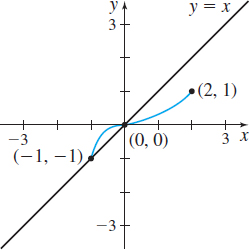
Question
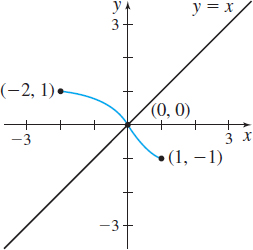
Question
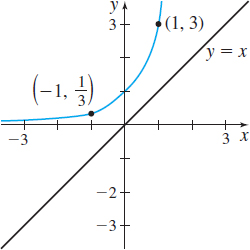
Question
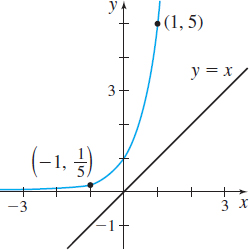
In Problems 29–38, the function f is one-to-one.
- Find its inverse and check the result.
- Find the domain and the range of f and the domain and the range of \(f^{-1}\).
Question
\(f(x) = 4x + 2\)
Question
\(f(x) = 1-3x\)
Question
\(f(x) = \sqrt[3]{x+10}\)
Question
\(f(x) = 2x^{3}+4\)
Question
\(f(x) = \dfrac{1}{x-2}\)
Question
\(f(x) = \dfrac{2x}{3x-1}\)
Question
\(f(x) = \dfrac{2x+3}{x+2}\)
Question
\(f(x) = \dfrac{-3x-4}{x-2}\)
Question
\(f(x) = x^{2}+4\), \(x\geq 0\)
Question
\(f(x) = (x-2)^{2}+4\), \(x\leq 2\)
