Chapter 13

Section 13.1

1. True

2. True

3. False

4. True

5. False

6.

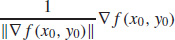
7. −▽ f (x₀, y₀)

8.

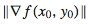
9. (a)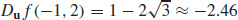

(b) Starting at the point (−1, 2) and moving in the direction u = 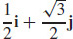, the function is changing at a rate of approximately −2.46 units per unit length.

(c) The slope of the tangent line to the curve C that is the intersection of the surface f (x, y) = xy² + x², and the plane perpendicular to the xy-plane that contains the line through point (−1, 2, 0) in the direction u = 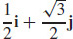, is approximately −2.46.

11. (a) D_uf(-1, 3) =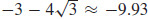

(b) Starting at the point (−1, 3) and moving in the direction θ = 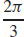, the function is changing at a rate of approximately −9.93 units per unit length.

(c) The slope of the tangent line to the curve C that is the intersection of the surface f (x, y) = 2xy − y², and the plane perpendicular to the xy-plane that contains the line through point (−1, 3, 0) in the direction θ = 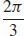, is approximately −9.93.

13. (a) D_uf(0, 0) =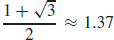

(b) Starting at the point (0, 0) and moving in the direction θ = 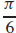, the function is changing at a rate of approximately 1.37 units per unit length.

(c) The slope of the tangent line to the curve C that is the intersection of the surface f(x, y) = xe^y + ye^x, and the plane perpendicular to the xy-plane that contains the line through point (0, 0, 0) in the direction θ = 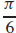, is approximately 1.37.

15. (a)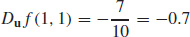

(b) Starting at the point (1, 1) and moving in the direction a = 3i − 4j, the function is changing at a rate of −0.7 units per unit length.

(c) The slope of the tangent line to the curve C that is the intersection of the surface 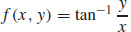, and the plane perpendicular to the xy-plane that contains the line through point (1, 1, 0) in the direction a = 3i − 4j, is −0.7.

17. (a) ▽ f(1, 2) = 6i + 4j

(b)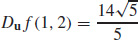

19. (a) ▽ f(0, 3) = 6i

(b)

21. (a) ▽ f(0, 1) = 2i

(b)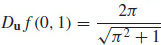

23. (a) ▽ f(1, 0) = j

(b)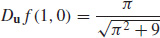

25. (a) ▽ f(2, 0) = 4i + 4j

(b) D_u f(2, 0) = 4

27. (a) ▽ f(0, 1, 2) = −4i

(b)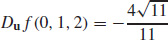

29. (a)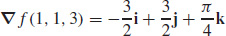

(b)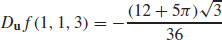

31. (a)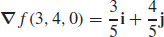

(b)

33. (a)

(b)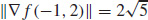

35. (a)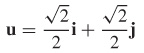

(b)

37. (a)

(b)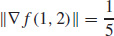

39. (a)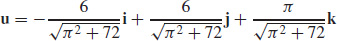

(b)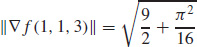

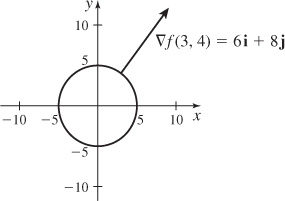
41.

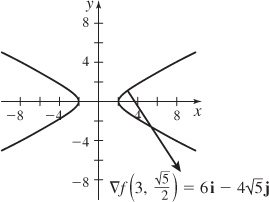
43.

45.

47. (a) The rate of change of temperature is 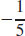◦C per unit length in the direction 3i – 4j.

(b) The temperature is increasing most rapidly in the direction \(\nabla T (0, 0) = {\bf i} + {\bf j} \).

(c) The temperature is decreasing most rapidly in the direction \(-\nabla T (0, 0) = -{\bf i} - {\bf j} \).

(d) The rate of change of temperature remains the same in the directions \(-{\bf i}+{\bf j}\) and \({\bf i}-{\bf j}\).

49. Water will flow in the direction \(-\nabla{\bf z}(1,2)=4{\bf i}+4{\bf j}\).

51. The rate of change of temperature is 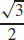◦C per unit of distance in the u-direction.

53. (a) The direction is .

(b) See Student Solutions Manual.

(c) The maximum rate of change is .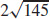

55. Vector is normal to the level curve of f at P, as is

57. (a) The level curves are circles of the form x² + y² = .

(b)

(c) The level curve x² + y² = 25.

(d)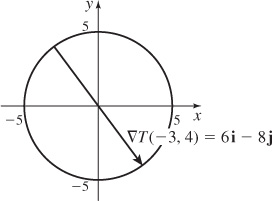

(e) Answers will vary.

59. The charge moves in the direction 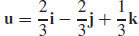. The electrical potential changes at a rate of −3e⁻² volts per unit change in the u-direction.

61.

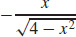
63. See Student Solutions Manual.

65. See Student Solutions Manual.

67. See Student Solutions Manual.

69. See Student Solutions Manual.

71. Function f is not necessarily differentiable. See Student Solutions Manual.

73. See Student Solutions Manual.

75. See Student Solutions Manual.

77. See Student Solutions Manual.

Section 13.2

1. True

2. True

3. 4y + z = 14

5. 8x + 18y − z = 13

7. (a) x − 2y + 3z = 14

(b)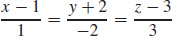

9. (a) 4x + y + 2z = 3

(b)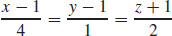

11. (a) 4x − 2y + z = −5

(b)

13. (a) 4x − z = 2

(b)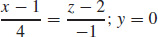

15. (a) 3x − 3y − 4z = 2

(b)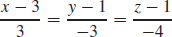

17. (a)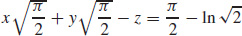

(b)

19. (a) y + z =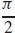

(b)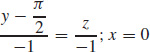

(c)

21. (a) 2x + y − z = 18

(b)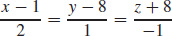

(c)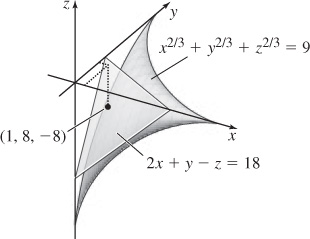

23. See Student Solutions Manual.

25. The tangent plane is parallel to the xy-plane at (x, y, z) = (3,−1, 11).

27. The tangent plane is parallel to the xy-plane for all (x, y, z) such that y = −x and z = 0.

29. The tangent plane is parallel to the xy-plane at (x, y, z) = (0, −1, 1), 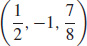and .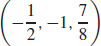

31. The engineer should drill in the direction .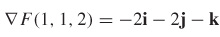

33. (a) See Student Solutions Manual.

(b)

35. See Student Solutions Manual.

37. The equation of the tangent plane is y + z = π. The symmetric equations for the normal line are .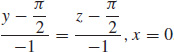

39. See Student Solutions Manual.

41. See Student Solutions Manual.

43. An equation of the tangent plane is (ln 2)x + 2y + (1 + ln 2)z = 4(1 + ln 2). Symmetric equations of the normal line are .

Section 13.3

1. (a)

2. f_x (x, y) = f_y(x, y) = 0.

3. False

4. (c)

5. True

6. boundary

7. The critical points are (0, 0),(1, 0), and (−1, 0).

9. The critical points are (0, 0),(1, 1), and (−1,−1).

11. There are no critical points.

13. There is a local minimum at (1,−2); the local minimum value is z = −3.

15. There is a local minimum at (2,−1); the local minimum value is z = −9.

17. The point (0, 0, 0) is a saddle point of z. There is a local minimum at (2, 2); the local minimum value is z = −8.

19. The point (0, 2, 4) is a saddle point of z.

21. The point (0, 0, 0) is a saddle point of z. There is a local maximum at (−1,−1); the local maximum value is z = 1.

23. The points (3,−4.5, 6.75) and (0, 0, 0) are saddle points of z.

25. There are no critical points.

27. The function has critical points at (x, y) = (mπ, nπ) for integers m and n. For odd values of m and n, the function has a local minimum; the local minimum value is z = −2. For even values of m and n, the function has a local maximum; the local maximum value is z = 2. For odd m and even n OR even m and odd n, (mπ, nπ, 0) is a saddle point of z.

29. For integer n, the function has a local minimum at (2πn, 3) and (π + 2πn,−3); the local minimum value is −3. For integer n, the points 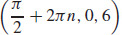and 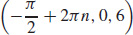are saddle points of z.

31. The point (0, 0, 1) is a saddle point of z.

33. The absolute maximum value of f is 4; the absolute minimum value of f is 0.

35. The absolute maximum value of f is 4 + 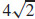; the absolute minimum value of f is −2.

37. The absolute maximum value of f is 33; the absolute minimum value of f is −7.

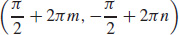39. For integers m and n, there are local minima at and ; the local minimum value is −1. For integers m and n, there are local maxima at 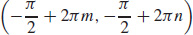and ; the local maximum value is 1. For integers m and n, (x, y, z) = (πm, πn, 0) are saddle points of z.

41. At its highest peak, the mountain is 14 km above sea level.

43. The volume is a maximum when the length and width are 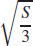and the depth is .

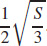45. The dimensions of the closed box of volume V = 500 cm³ that uses the least amount of material occur when the length, width, and depth are all cm.

47. (a) The rectangular box with maximum volume has a cross section of dimensions 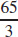inches by 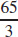inches and a length of 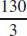inches.

(b) The cylindrical box with maximum volume has a radius of 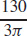inches and a length of 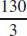inches.

49. (a) For a fixed amount x of Drug A, y = units of Drug B produces the maximum reaction.

(b) For a fixed amount y of Drug B, x = 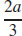units of Drug A produces the maximum reaction.

(c) Reaction is a maximum when x = 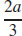units of Drug A and y = units of Drug B are used.

51. The location 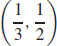will minimize the cost of connecting the plants to D.

53. The location with the highest reading is .

55. Production is maximized when 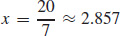thousand units are sold at a price of 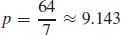thousand dollars and thousand units are sold at a price of 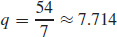thousand dollars. The maximum profit is $18,286.

57. See Student Solutions Manual.

59. (a) See Student Solutions Manual.

(b) The equation of the least squares estimate is y = 0.7x + 1.2.

Section 13.4

1. (c)

2. True

3. False

4. False

5. The maximum value of f is 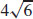. The minimum value of f is .

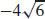7. The maximum value of f is 4 + . The minimum value of f is 4 − .

9. The maximum value of f is 1. The minimum value of f is .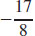

11. The maximum value of f is 2. The minimum value of f is −2.

13. The maximum value of f is 20. The minimum value of f is 0.

15. The minimum value of f is .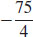

17. The absolute minimum value of f is −2. The absolute maximum value of f is 6.

19. The absolute minimum value of f is 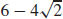. The absolute maximum value of f is .

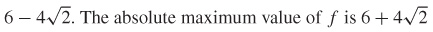21. The point is closest to the origin.

23. The maximum product is .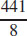

25. (a) The points (0, 3, 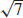) and (0, 3, ) are farthest from the origin.

(b) The points and 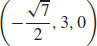are closest to the origin.

27. The product is a maximum at 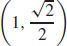and .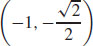

29. The optimal dimensions are obtained when 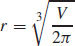and .

31. An open-topped box with a square base of 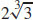m by 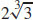m and a height of 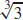m will minimize the cost.

33. A cubical suitcase with each side measuring 15 inches will maximize the volume.

35. (a) Width x must be no less than 20 m and no more than 50 m.

(b) The greatest number of square meters that can be enclosed by the two fields is 3400 m².

37. Production levels of x = 1800 thousand units and y = 3600 thousand units will minimize production cost.

39. (a) Invest 250 units of capital and 1050 units of labor to maximize production.

(b) The maximum production is 740.8 units.

41. The minimum value of w is 9.

43. See Student Solutions Manual.

45. On the union of the two curves, f attains a maximum value at (±1, 0) and (0, ±1) and a minimum value at .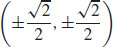

47.

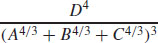
49.

Review Exercises

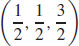
1.

3.

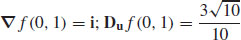
5.

7. (a)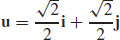

(b) 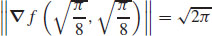is the maximum value; is the minimum value.

9. (a) u = i

(b) ||∇ f(0, 1)|| = 1 is the maximum value; −||∇ f(0, 1)|| = −1 is the minimum value.

11. (a) 4x − z = 2

(b)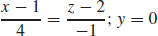

13. The critical point is (−4, 2).

15. The critical point is (0, 0).

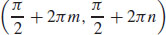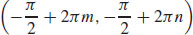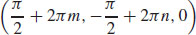17. For integers m and n, there is a local maximum value at ; the local maximum value is z = 2. For integers m and n, there is a local minimum value at ; the local minimum value is z = −2. For integers m and n, and are saddle points of z.

19. The absolute maximum value is 9; the absolute minimum value is −7.

21. There is a minimum value at 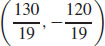; the minimum value is z = .

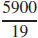23. There is a minimum value at 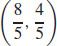; the minimum value is z = .

25. (a)

(b) The temperature is increasing most rapidly in the direction u = .

(c) The temperature is decreasing most rapidly in the direction u = .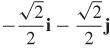

(d) The rate of change of temperature is 0 in the directions u = 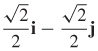and u = .

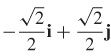27. (a) Invest 306 units of capital and 357 units of labor to maximize production.

(b) The maximum production is 3408.7 units.

29. The points (1, 1, 1), (−1, 1,−1), (−1,−1, 1), and (1,−1,−1) are all closest to the origin.

31. A box with a square base with each side measuring and a height of will minimize the total cost of the box.