1.5 Infinite Limits; Limits at Infinity; Asymptotes
117
OBJECTIVES
When you finish this section, you should be able to:
- Investigate infinite limits (p. 117)
- Find the vertical asymptotes of a function (p. 119)
- Investigate limits at infinity (p. 120)
- Find the horizontal asymptotes of a function (p. 125)
- Find the asymptotes of a rational function using limits (p. 126)
RECALL
The symbols \(\infty\) (infinity) and \(-\infty\) (negative infinity) are not numbers. The symbol \(\infty\) expresses unboundedness in the positive direction, and \(-\infty\) expresses unboundedness in the negative direction.
We have described \(\lim\limits_{x\rightarrow c}f(x) = L\) by saying if a function \(f\) is defined everywhere in an open interval containing \(c\), except possibly at \(c\), then the value \(f(x)\) can be made as close as we please to \(L\) by choosing numbers \(x\) sufficiently close to \(c\). In this section, we extend the language of limits to allow \(c\) to be \(\infty\) or \(-\infty \) (limits at infinity) and to allow \(L\) to be \(\infty \) or \(-\infty \) (infinite limits). These limits are useful for locating asymptotes that aid in graphing some functions.
Limits at infinity have practical use in many fields. They are used to determine what happens in the long run. For example, environmentalists are often interested in the effects of development on the long-term population of a certain species.
We begin with infinite limits.
1 Investigate Infinite Limits
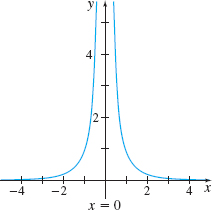
Consider the function \(f(x) = \dfrac{1}{x^{2}}\). Table 11 lists values of \(f\) for selected numbers \(x\) that are close to 0 and Figure 46 shows its graph.
| \(\underrightarrow{x~\hbox{approaches 0 from the left}}\) | \(\underleftarrow{x~\hbox{approaches 0 from the right}}\) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| \(x\) | \(-0.01\) | \(-0.001\) | \(-0.0001\) | \(\rightarrow\) | 0 | \(\leftarrow\) | \(0.0001\) | \(0.001\) | \(0.01\) |
| \(f(x) = \dfrac{1}{x^{2}}\) | \(10,000\) | \(1,000,000\) | \(100,000,000\) | \(f(x)\) becomes unbounded | \(100,000,000\) | \(1,000,000\) | \(10,000\) | ||
As \(x\) approaches \(0\), the value of \(\dfrac{1}{x^{2}}\) increases without bound. Since the value of \(\dfrac{1}{x^{2}}\) is not approaching a single real number, the limit of \(f(x)\) as \(x\) approaches \(0\) does not exist. However, since the numbers are increasing without bound, we describe the behavior of the function near zero by writing \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow 0}\frac{1}{x^{2}} = \infty} \] and say that \(f(x) = \dfrac{1}{x^{2}}\) has an infinite limit as \(x\) approaches \(0\).
In other words, a function \(f\) has an infinite limit at \(c\) if \(f\) is defined everywhere in an open interval containing \(c\), except possibly at \(c\), and \(f(x)\) becomes unbounded when \(x\) is sufficiently close to \(c\). *
*A precise definition of an infinite limit is given in Section 1.6.
As a second example, consider the function \(f(x) = \dfrac{1}{x}\). Table 12 shows values of \(f\) for selected numbers \(x\) that are close to \(0\) and Figure 47 shows its graph.
118

| \(\underrightarrow{x~\hbox{approaches 0 from the left}}\) | \(\underleftarrow{x~\hbox{approaches 0 from the right}}\) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(x\) | \(-0.01\) | \(-0.001\) | \(\ -0.0001\) | \(\rightarrow \) | 0 | \(\leftarrow\) | \(0.0001\) | \(0.001\) | \(0.01\) | \(0.1\) |
| \(f( x) =\dfrac{1}{x}\) | \(-100\) | \(-1000\) | \(\ -10{,}000\) | \(f(x)\) becomes unbounded | \(\ 10{,}000\) | \(1000\) | \(100\) | \(10\) | ||
Here as \(x\) gets closer to \(0\) from the right, the value of \(f(x)=\dfrac{1}{x}\) can be made as large as we please. That is, \(\dfrac{1}{x}\) becomes unbounded in the positive direction. So, \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow 0^{+}}\frac{1}{x}=\infty} \]
Similarly, the notation \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow 0^{-}}\frac{1}{x}=-\infty} \]
is used to indicate that \(\dfrac{1}{x}\) becomes unbounded in the negative direction as \(x\) approaches \(0\) from the left.
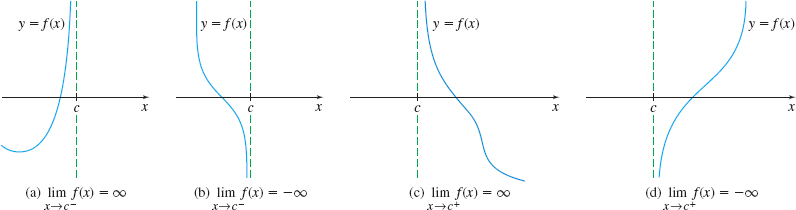
So, there are four possible one-sided infinite limits of a function \(f\) at \(c\): \[ \begin{equation*} \lim_{x\rightarrow c^{-}}f(x)=\infty,\qquad \lim_{x\rightarrow c^{-}}f(x)=-\infty,\qquad \lim_{x\rightarrow c^{+}}f(x)=\infty,\qquad \!\lim_{x\rightarrow c^{+}}f(x)=-\infty \end{equation*} \]
See Figure 48 for illustrations of these possibilities.
Investigating an Infinite Limit
Investigate \(\lim\limits_{x\rightarrow 0^{+}}\ln x\).
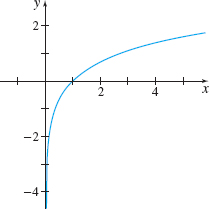
Solution The domain of \(f(x)=\ln x\) is \(\{x|x>0\}\). Notice that the graph of \(f(x)=\ln x\) in Figure 49 decreases without bound as \(x\) approaches \(0\) from the right. The graph suggests that \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow 0^{+}}\ln x=-\infty} \]
NOW WORK
Problem 27.
Based on the graphs of the trigonometric functions in Figure 50, we have the following infinite limits: \begin{equation*} \begin{array}{rcl@{\hspace*{8pt}}rcl@{\hspace*{8pt}}rcl@{\hspace*{8pt}}rcl} \lim\limits_{x\rightarrow {\pi }/{2}^{-}}\tan x&=&\infty & \lim\limits_{x\rightarrow {\pi }/{2}^{+}}\tan x&=&-\infty & \lim\limits_{x\rightarrow {\pi }/{2}^{-}}\sec x&=&\infty & \lim\limits_{x\rightarrow {\pi }/{2}^{+}}\sec x&=&-\infty \\[14pt] \lim\limits_{x\rightarrow 0^{-}}\csc x&=&-\infty & \lim\limits_{x\rightarrow 0^{+}}\csc x&=&\infty & \lim\limits_{x\rightarrow 0^{-}}\cot x&=&-\infty & \lim\limits_{x\rightarrow 0^{+}}\cot x&=&\infty \end{array} \end{equation*}
119

2 Find the Vertical Asymptotes of a Function
Figure 51 illustrates the possibilities that can occur when a function has an infinite limit at \(c\). In each case, notice that the graph of \(f\) has a vertical asymptote at \(c\).

spanDEFINITIONspan Vertical Asymptote
The line \(x=c\) is a vertical asymptote of the graph of the function \(f\) if any of the following is true: \begin{equation*} \begin{array}{l} \lim\limits_{^{{}}x\rightarrow c^{-}}f(x)=\infty\qquad \lim\limits_{^{{}}x \rightarrow c^{+}}f(x)=\infty\qquad \lim\limits_{^{{}}x\rightarrow c^{-}}f(x)=-\infty\qquad \lim\limits_{^{{}}x\rightarrow c^{+}}f(x)=-\infty \end{array} \end{equation*}
For rational functions, vertical asymptotes may occur where the denominator equals 0.
Finding a Vertical Asymptote
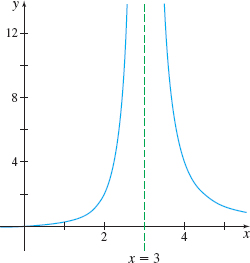
Find any vertical asymptote(s) of the graph of \(f(x)=\dfrac{x}{(x-3)^{2}}\).
Solution The domain of \(f\) is \(\{x|x\neq 3\}\). Since \(3\) is the only number for which the denominator of \(f\) equals zero, we construct Table 13 and investigate the one-sided limits of \(f\) as \(x\) approaches \(3\). Table 13 suggests that \[ \lim\limits_{x\rightarrow 3}\dfrac{x}{(x-3)^{2}}=\infty \]
So, \(x=3\) is a vertical asymptote of the graph of \(f\).
| \(\underrightarrow{x~\hbox{approaches 3 from the left}}\) | \(\underleftarrow{x~\hbox{approaches 3 from the right}}\) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| \(x\) | \(2.9\) | \(2.99\) | \(2.999\) | \(\ \rightarrow \) | 3 | \(\leftarrow\) | \(3.001\) | \(3.01\) | \(3.1\) |
| \(f( x) =\dfrac{x}{(x-3)^{2}}\) | \(290\) | \(29{,}900\) | \(2{,}999{,}000\) | \(f(x)\) becomes unbounded | \(3{,}001{,}000\) | \(30{,}100\) | \(310\) | ||
120
Figure 52 shows the graph of \(f( x) =\dfrac{x}{( x-3)^{2}}\) and its vertical asymptote.
NOW WORK
Problems 15 and 63 (find any vertical asymptotes).
3 Investigate Limits at Infinity
Now we investigate what happens as \(x\) becomes unbounded in either the positive direction or the negative direction. Suppose as \(x\) becomes unbounded, the value of a function \(f\) approaches some real number \(L\). Then the number \(L\) is called the limit of \(f\) at infinity.
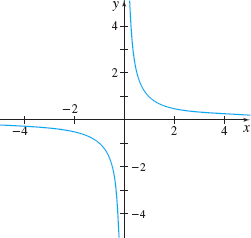
For example, the graph of \(f( x) =\dfrac{1}{x}\) in Figure 53 suggests that, as \(x\) becomes unbounded in either the positive direction or the negative direction, the values \(f(x)\) get closer to \(0\). Table 14 illustrates this for a few numbers \(x\).
| \(x\) | \(\pm 100\) | \(\pm 1000\) | \(\pm 10{,}000\) | \(\pm 100{,}000\) | \(x\) becomes unbounded |
| \(f( x) =\dfrac{1}{x}\) | \(\pm 0.01\) | \(\pm 0.001\) | \(\pm 0.0001\) | \(\pm 0.00001\) | \(f(x)\) approaches \(0\) |
Since \(f\) can be made as close as we please to \(0\) by choosing \(x\) sufficiently large, we write \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow \infty }\dfrac{1}{x}=0} \]
and say that the limit as \(x\) approaches infinity of \(f\) is equal to \(0\) . Similarly, as \(x\) becomes unbounded in the negative direction, the function \(f(x)=\dfrac{1}{x}\) can be made as close as we please to \(0\), and we write \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow -\infty }\dfrac{1}{x}=0} \]
Although we do not prove \(\lim\limits_{x\rightarrow -\infty }\dfrac{1}{x}=0\) here, it can be proved using the \(\epsilon\)-\(\delta\) Definition of a Limit at Infinity, and is left as an exercise in Section 1.6.
The limit properties discussed in Section 1.2, with “\( x\rightarrow c\)” replaced by “\( x\rightarrow \infty \)” or “\(x\rightarrow -\infty \),” hold for infinite limits. Although these properties are stated below for limits as \(x\rightarrow \infty\), they are also valid for limits as \(x\rightarrow -\infty\).
THEOREM Properties of Limits at Infinity
If \(k\) is a real number, \(n\geq 2\) is an integer, and the functions \(f\) and \(g\) approach real numbers as \(x\rightarrow \infty\), then the following properties are true:
- \(\lim\limits_{x\rightarrow \infty }A=A\) where \(A\) is a real number
- \(\lim\limits_{x\rightarrow \infty }\left[ kf(x)\right]=k\lim\limits_{x\rightarrow \infty }f(x)\)
- \(\lim\limits_{x\rightarrow \infty }[f(x)\pm g(x)]=\lim\limits_{x\rightarrow \infty }f(x)\pm \lim\limits_{x\rightarrow \infty }g(x)\)
- \(\lim\limits_{x\rightarrow \infty }[f(x)g(x)]=\left[ \lim\limits_{\kern.5ptx\rightarrow \infty }f(x)\right] \left[ \lim\limits_{\kern.5ptx\rightarrow \infty }g(x)\right]\)
- \(\lim\limits_{x\rightarrow \infty }\dfrac{f(x)}{g(x)}=\dfrac{\lim\limits_{x\rightarrow \infty }f(x)}{\lim\limits_{x\rightarrow \infty}g(x)}\), provided \(\lim\limits_{x\rightarrow \infty }g(x)\neq 0\)
- \(\lim\limits_{x\rightarrow \infty }[f(x)]^{n}=\left[ \lim\limits_{\kern.5ptx\rightarrow \infty }f(x)\right] ^{n}\)
- \(\lim\limits_{x\rightarrow \infty }\sqrt[n]{f(x)}=\sqrt[n]{\lim\limits_{x\rightarrow \infty }f(x)}\), where \(f(x)\geq 0\) if \(n\) is even
121
Finding Limits at Infinity
Find:
- \(\lim\limits_{x\rightarrow -\infty }\dfrac{4}{x^{2}}\)
- \(\lim\limits_{x\rightarrow \infty }\left( -\dfrac{10}{\sqrt{x}} \right)\)
- \(\lim\limits_{x\rightarrow \infty }\left( 2+\dfrac{3}{x}\right)\)
Solution (a)\(\lim\limits_{x\rightarrow -\infty }\dfrac{4}{x^{2}}=4\left(\lim\limits_{x\rightarrow -\infty }\dfrac{1}{x}\right)^2=4\,{\cdot}\,0=0\)
(b)\(\lim\limits_{x\rightarrow \infty }\left( -\dfrac{10}{\sqrt{x}}\right) =-10\lim\limits_{x\rightarrow \infty }\dfrac{1}{\sqrt{x}}=-10\,{\cdot}\,\lim\limits_{x\rightarrow \infty }\sqrt{\dfrac{1}{x}}=-10\,{\cdot}\,\sqrt{\lim\limits_{x\rightarrow \infty }\dfrac{1}{x}}\) \(=-10\,{\cdot}\,0=0\)
(c) \(\lim\limits_{x\rightarrow \infty }\left( 2+\dfrac{3}{x}\right) =\lim\limits_{x\rightarrow \infty }2+\lim\limits_{x\rightarrow \infty } \dfrac{3}{x}=2+3\cdot \lim\limits_{x\rightarrow \infty }\dfrac{1}{x} =2+3\cdot 0=2\)
NOW WORK
Problem 45.
Finding Limits at Infinity
Find:
- \(\lim\limits_{x\rightarrow \infty }\) \(\dfrac{3x^{2}-2x+8}{x^{2}+1}\)
- \(\lim\limits_{x\rightarrow -\infty }\dfrac{4x^{2}-5x}{x^{3}+1}\)
Solution (a) We find this limit by dividing each term of the numerator and the denominator by the term with the highest power of \(x\) that appears in the denominator, in this case, \(x^{2}\). Then \[ \begin{eqnarray*} \lim\limits_{x\rightarrow \infty }\dfrac{3x^{2}\,{-}\,2x\,{+}\,8}{x^{2}+1}\hspace{-2.8pc}\underset{\underset{\color{#0066A7}{\raise-12pt\scriptsize\hbox{Divide the numerator and }}}{\color{#0066A7}{\uparrow}}}{=}\hspace{-3pc}\lim\limits_{x\rightarrow \infty }\dfrac{\dfrac{ 3x^{2}\,{-}\,2x\,{+}\,8}{x^{2}}}{\dfrac{x^{2}+1}{x^{2}}}&=&\lim\limits_{x\rightarrow \infty }\dfrac{3\,{-}\,\dfrac{2}{x}\,{+}\,\dfrac{8}{x^{2}}}{1+\dfrac{1}{x^{2}}}\hbox{ }\hspace{-2.5pc} \underset{\raise-5pt\underset{\color{#0066A7}{\raise-13pt\scriptsize\hbox{Limit of a Quotient}}}{\color{#0066A7}{\uparrow}}}{=}\hspace{-2pc}\dfrac{\lim\limits_{x\rightarrow \infty }\left[ 3\,{-}\,\dfrac{2}{x}\,{+}\,\dfrac{8}{x^{2}}\right] }{\lim\limits_{x\rightarrow \infty }\left[ 1+\dfrac{1 }{x^{2}}\right] }\\[-1pc] \hspace{-8pc}{\color{#0066A7}{\scriptsize\hbox{denominator by \(x^{2}\)}}} \\ &&\\[-21pc] &=&\dfrac{\lim\limits_{x\rightarrow \infty }3-\lim\limits_{x\rightarrow \infty }\dfrac{2}{x}+\lim\limits_{x\rightarrow \infty }\dfrac{8}{x^{2}}}{\lim\limits_{x\rightarrow \infty }1+\lim\limits_{x\rightarrow \infty }\dfrac{1}{x^{2}}}=\dfrac{ 3-2\lim\limits_{x\rightarrow \infty }\dfrac{1}{x}+8\left(\lim\limits_{x\rightarrow \infty }\dfrac{1}{x}\right)^2}{1+\left(\lim\limits_{x\rightarrow \infty }\dfrac{1}{x}\right)^2}\\[3pt] &=&\dfrac{3-0+0}{1+0}=3 \end{eqnarray*} \]
(b) \[ \lim\limits_{x\rightarrow -\infty }\dfrac{4x^{2}-5x}{ x^{3}+1}\hspace{-3pc}\raise-4pt\underset{\underset{\color{#0066A7}{\scriptsize\hbox{Divide the numerator and}}}{\color{#0066A7}{\uparrow}}} {=}\hspace{-2.9pc}\lim\limits_{x\rightarrow -\infty }\dfrac{\dfrac{4x^{2}-5x}{x^{3}}}{\dfrac{x^{3}+1}{x^{3}}} =\lim\limits_{x\rightarrow -\infty }\dfrac{\dfrac{4}{x}-\dfrac{5}{x^{2}}}{1+ \dfrac{1}{x^{3}}}=\dfrac{\lim\limits_{x\rightarrow -\infty }\left( \dfrac{4}{ x}-\dfrac{5}{x^{2}}\right) }{\lim\limits_{x\rightarrow -\infty }\left( 1+ \dfrac{1}{x^{3}}\right) }=\dfrac{0}{1}=0\\[-20pt] \hspace{-15pc}{\raise0pt\color{#0066A7}{\scriptsize\hbox{denominator by \(x^{3}\)}}} \]
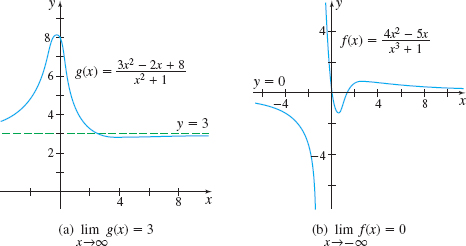
The graphs of the functions \(g(x) =\dfrac{3x^{2}-2x+8}{x^{2}+1}\) and \(f( x) =\dfrac{4x^{2}-5x}{x^{3}+1}\) are shown in Figures 54(a) and 54(b), respectively. In each graph, notice how the graph of the function behaves as \(x\) becomes unbounded.
122
NOW WORK
Problems 47 and 49.
Limits at infinity have the following property.
If \(p>0\) is a rational number and \(k\) is any real number, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow \infty }\dfrac{k}{x^{p}}=0 \qquad\hbox{ and } \qquad \lim\limits_{x\rightarrow -\infty }\dfrac{k}{x^{p}}=0 } \] provided \(x^{p}\) is defined when \(x\lt 0\).
For example, \(\lim\limits_{x\rightarrow \infty }\dfrac{5}{x^{3}}=0\), \(\lim\limits_{x\rightarrow \infty }\dfrac{-6}{x^{2/3}}=0\), and \(\lim\limits_{x\rightarrow -\infty }\dfrac{4}{x^{8/3}}=0\).

Finding the Limit at Infinity
Find \(\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt{4x^{2}+10}}{x-5}\).
Solution Divide each term of the numerator and the denominator by \(x\), the term with the highest power of \(x\) that appears in the denominator. But remember, since \(\sqrt{x^{2}}=\vert x\vert =x\) when \(x\geq 0\), in the numerator the divisor in the square root will be \(x^{2}\). \[ \begin{eqnarray*} \lim\limits_{x\rightarrow \infty }\dfrac{\sqrt{4x^{2}+10}}{x-5} &=&\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt{\dfrac{4x^{2}+10}{x^{2}} }}{\dfrac{x-5}{x}}=\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt{\dfrac{ 4x^{2}}{x^{2}}+\dfrac{10}{x^{2}}}}{1-\dfrac{5}{x}}= \dfrac{\lim\limits_{x\rightarrow \infty }\sqrt{4+ \dfrac{10}{x^{2}}}}{\lim\limits_{x\rightarrow \infty }\left[ 1-\dfrac{5}{x} \right] } \\ &=&{\sqrt{\lim\limits_{x\rightarrow \infty }\left[ 4+\dfrac{10}{x^{2}}\right] }}={\sqrt{4}} =2 \end{eqnarray*} \]
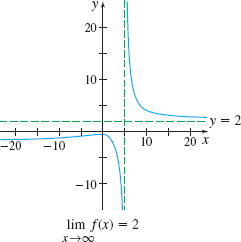
The graph of \(f( x) =\dfrac{\sqrt{4x^{2}+10}}{x-5}\) and its behavior as \(x\rightarrow \infty \) is shown in Figure 55.
NOW WORK
Problem 57.
Infinite Limits at Infinity
In each of the examples above, \(f( x)\) approached a real number as \(x\) became unbounded in either the positive or the negative direction. There are times, however, that this is not the case.
123
For example, consider the function \(f(x) =x^{2}\). As \(x\) becomes unbounded in either the positive or negative direction, \(f( x)\) increases without bound, as Figure 56 and Table 15 suggest. If a function grows without bound as \(x\) becomes unbounded, we say that \(f\) has an infinite limit at infinity.
| \(x\) | \(\pm 100\) | \(\pm 1000\) | \(\pm 10{,}000\) | \(x\) becomes unbounded |
| \(f(x) =x^{2}\) | 10,000 | 1,000,000 | 100,000,000 | \(f(x)\) becomes unbounded |
Compare the graph of \(f( x) =x^{2}\) in Figure 56 to the graph of \(g( x) =x^{3}\) shown in Figure 57. As \(x\) becomes unbounded in the positive direction, \(g\) increases without bound, but as \(x\) becomes unbounded in the negative direction \(g\) becomes unbounded in the negative direction.


Infinite limits at infinity can take on any of the following four forms: \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow \infty }f( x) =\infty\qquad\!\!\!\! \lim\limits_{x\rightarrow \infty }f( x) =-\infty\qquad\!\!\!\! \lim\limits_{x\rightarrow -\infty }f( x) =\infty\qquad\!\!\!\! \lim\limits_{x\rightarrow -\infty }f( x) =-\infty} \]
Finding a Limit at Infinity
Find \(\lim\limits_{x\rightarrow \infty }\dfrac{5x^{4}-3x^{2}}{2x^{2}+1}\).

Solution \(R( x) =\dfrac{5x^{4}-3x^{2}}{2x^{2}+1}\) is a rational function defined for all real numbers. Find the limit by dividing each term of the numerator and the denominator by the term with the highest power of \(x\) that appears in the denominator, in this case, \(2x^{2}\). Then \[ \begin{eqnarray*} \lim\limits_{x\rightarrow \infty }\dfrac{5x^{4}-3x^{2}}{2x^{2}+1} \underset{\underset{\underset{\color{#0066A7}{\hbox{and denominator by \(2x^{2}\)}}}{\color{#0066A7}{\hbox{Divide the numerator}}}}{\color{#0066A7}{\uparrow}}}{=}\lim\limits_{x\rightarrow \infty }\dfrac{ \dfrac{5x^{4}-3x^{2}}{2x^{2}}}{\dfrac{2x^{2}+1}{2x^{2}}}=\lim\limits_{x \rightarrow \infty }\dfrac{\dfrac{5x^{2}}{2}-\dfrac{3}{2}}{1+\dfrac{1}{2x^{2} }}=\infty \end{eqnarray*} \]
because \(\dfrac{5x^{2}}{2}-\dfrac{3}{2}\) \(\rightarrow \infty \) and \(1+\dfrac{ 1}{2x^{2}}\) \(\rightarrow \) \(1\) as \(x\rightarrow \infty \).
The graph of \(R\) is shown in Figure 58.
NOW WORK
Problem 59.
124
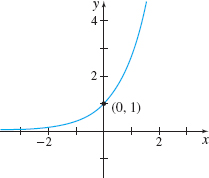
The graph of the exponential function, shown in Figure 59, suggests that \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow -\infty }e^{x}=0\qquad \lim\limits_{x\rightarrow \infty }e^{x}=\infty} \]
These limits are supported by the information in Table 16.
| \(x\) | \(-1\) | \(-5\) | \(-10\) | \(-20\) | \(x\) approaches \(-\infty\) |
| \(f(x) =e^{x}\) | 0.36788 | 0.00674 | 0.00005 | \(-2\times 10^{-9}\) | \(f(x)\) approaches 0 |
| \(x\) | 1 | 5 | 10 | 20 | \(x\) approaches \(\infty \) |
| \(f(x) =e^{x}\) | \(e\approx 2.71812\) | 148.41 | 22,026 | \(4.85\times 10^{8}\) | \(f(x)\) becomes unbounded |
Finding the Limit at Infinity of \(f(x)=\ln x\)
Find \(\lim\limits_{x\rightarrow \infty }\ln x\).
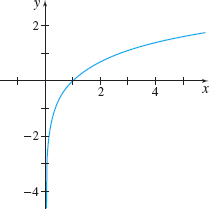
Solution Table 17 and the graph of \(f( x) =\ln x\) in Figure 60 suggest that \(\ln x\) has an infinite limit at infinity. That is, \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow \infty }\ln x =\infty} \]
| \(x\) | \(e^{10}\) | \(e^{100}\) | \(e^{1000}\) | \(e^{10{,}000}\) | \(e^{100{,}000}\) | \(\rightarrow x\) becomes unbounded |
| \(f( x) =\ln x\) | 10 | 100 | 1000 | 10,000 | 100,000 | \(\rightarrow f(x)\) becomes unbounded |
Application: Decomposition of Salt in Water
Salt (NaCl) decomposes in water into sodium (Na\(^{+})\) ions and chloride (Cl\( ^{-})\) ions according to the law of uninhibited decay \begin{equation*} A( t) =A_{0}e^{kt} \end{equation*}
where \(A=A( t) \) is the amount (in kilograms) of salt present at time \(t\) (in hours), \(A_{0}\) is the original amount of salt in the solution, and \(k\) is a negative number that represents the rate of decomposition.
- If initially there are 25 kilograms (kg) of salt and after 10 hours (h) there are 15 kg of salt remaining, how much salt is left after one day?
- How long will it take until \(\dfrac{1}{2} {kg}\) of salt remains?
- Find \(\lim\limits_{t\rightarrow \infty }A( t) \).
- Interpret the answer found in (c).
NEED TO REVIEW?
Solving exponential equations is discussed in Section P.5, pp. 45-46.
Solution
- Initially, there are 25 kg of salt, so \(A(0) =A_{0}=25\). To find the number \(k\) in \(A(t)=A_{0}e^{kt}\), we use the fact that at \(t=10\), then \(A(10) =15\). That is, \begin{eqnarray*} A( 10) &=&15=25e^{10k}\qquad {\color{#0066A7}{\hbox{\(A (t) =A_{0}{e}^{kt}, A_{0}=25; A(10)=15\)}}}\\[3pt] e^{10k} &=&\dfrac{3}{5} \\[3pt] 10k &=&\ln \dfrac{3}{5} \\[3pt] k &=&\dfrac{1}{10}\ln 0.6 \end{eqnarray*}
So, \(A(t)=25e^{(\frac{1}{10}\ln 0.6)t}\). The amount of salt that remains after one day (24 h) is \begin{equation*} A( 24) =25e^{(\frac{1}{10}\ln 0.6) 24}\approx 7.337 kilograms \end{equation*}
125
- We want to find \(t\) so that \(A(t) =\dfrac{1}{2} kg\). Then \begin{eqnarray*} \dfrac{1}{2} &=&25e^{(\frac{1}{10}\ln 0.6)t} \\[3pt] e^{(\frac{1}{10}\ln 0.6)t} &=&\dfrac{1}{50} \\[3pt] \left(\dfrac{1}{10}\ln 0.6\right)t &=&\ln \dfrac{1}{50} \\[3pt] t &\approx &76.582 \end{eqnarray*}
After approximately \(76.6{h}\), \(\dfrac{1}{2}{kg}\) of salt will remain.
- Since \(\dfrac{1}{10}\ln 0.6\approx -0.051\), we have \(\lim\limits_{t\rightarrow \infty }A( t) =\lim\limits_{t\rightarrow \infty }(25e^{-0.051t})=\lim\limits_{t\rightarrow \infty }\dfrac{25}{e^{0.051t} }=0\)
- As \(t\) becomes unbounded, the amount of salt in the water approaches 0 kg. Eventually, there will be no salt present in the water.
NOW WORK
Problem 79.
4 Find the Horizontal Asymptotes of a Function
Limits at infinity have an important geometric interpretation. When \( \lim\limits_{x\rightarrow \infty }f(x)=M\), it means that as \(x\) becomes unbounded in the positive direction, the value of \(f(x)\) can be made as close as we please to a number \(M\). That is, the graph of \(y=f(x)\) is as close as we please to the horizontal line \(y=M\) by choosing \(x\) sufficiently large. Similarly, \(\lim\limits_{x\rightarrow -\infty }f(x)=L\) means that the graph of \(y=f(x)\) is as close as we please to the horizontal line \(y=L\) for \(x\) unbounded in the negative direction. These lines are horizontal asymptotes of the graph of \(f.\)
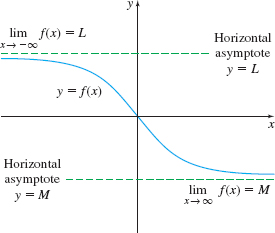
spanDEFINITIONspan Horizontal Asymptote
The line \(y=L\) is a horizontal asymptote of the graph of a function \(f\) for \(x\) unbounded in the negative direction if \(\lim\limits_{x\rightarrow -\infty }f(x)=L\).
The line \(y=M\) is a horizontal asymptote of the graph of a function \(f\) for \(x\) unbounded in the positive direction if \(\lim\limits_{x\rightarrow \infty }f(x)=M.\)
In Figure 61, \(y=L\) is a horizontal asymptote as \(x\rightarrow -\infty \) because \(\lim\limits_{x\rightarrow -\infty }f(x)=L\). The line \(y=M\) is a horizontal asymptote as \(x\rightarrow \infty \) because \(\lim\limits_{x\rightarrow \infty }f(x)=M\). To identify horizontal asymptotes, we find the limits of \(f\) at infinity.
Finding the Horizontal Asymptotes of a Function
Find the horizontal asymptotes, if any, of \(f(x)=\dfrac{3x-2}{4x-1}.\)
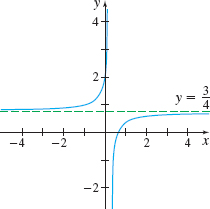
Solution We examine the two limits at infinity: \( \lim\limits_{x\rightarrow -\infty }\dfrac{3x-2}{4x-1}\) and \( \lim\limits_{x\rightarrow \infty }\dfrac{3x-2}{4x-1}.\)
Since \(\lim\limits_{x\rightarrow -\infty }\dfrac{3x-2}{4x-1}=\dfrac{3}{4},\) the line \(y=\dfrac{3}{4}\) is a horizontal asymptote of the graph of \(f\) for \( x\) unbounded in the negative direction.
Since \(\lim\limits_{x\rightarrow \infty }\dfrac{3x-2}{4x-1}=\dfrac{3}{4},\) the line \(y=\dfrac{3}{4}\) is a horizontal asymptote of the graph of \(f\) for \( x\) unbounded in the positive direction.
Figure 62 shows the graph of \(f(x)=\dfrac{3x-2}{4x-1}\) and the horizontal asymptote \(y=\dfrac{3}{4}.\)
NOW WORK
Problem 63 (find any horizontal asymptotes).
5 Find the Asymptotes of a Rational Function Using Limits
126
In the next example we find the horizontal asymptotes and vertical asymptotes, if any, of a rational function.
Finding the Asymptotes of a Rational Function Using Limits
Find any asymptotes of the rational function \(R(x)=\dfrac{3x^{2}-12}{ 2x^{2}-9x+10}\).
Solution We begin by factoring \(R.\) \begin{equation*} R(x)=\dfrac{3x^{2}-12}{2x^{2}-9x+10}=\dfrac{3(x-2)(x+2)}{(2x-5)(x-2)} \end{equation*}
The domain of \(R\) is \(\left\{ x |\ x\neq \dfrac{5}{2}\hbox{ and }x\neq 2\right\} \). Since \(R\) is a rational function, it is continuous on its domain, that is, all real numbers except \(x=\dfrac{5}{2}\) and \(x=2\).
To check for vertical asymptotes, we find the limits as \(x\) approaches \( \dfrac{5}{2}\) and \(2\). First we consider \(\lim\limits_{x\rightarrow \frac{ 5}{2}^{-}}R(x)\). \begin{equation*} \lim\limits_{x\rightarrow \frac{5}{2}^{-}}R(x)=\!\!\lim\limits_{x\rightarrow \frac{5}{2}^{-}}\left[ \frac{3(x-2)(x+2)}{(2x-5)(x-2)}\right] =\!\!\lim\limits_{x\rightarrow \frac{5}{2}^{-}}\left[ \frac{3(x+2)}{(2x-5)} \right] =3\!\!\lim\limits_{x\rightarrow \frac{5}{2}^{-}}\frac{x+2}{2x-5}=-\infty \end{equation*}
That is, as \(x\) approaches \(\dfrac{5}{2}\) from the left, \(R\) becomes unbounded in the negative direction.
The graph of \(R\) has a vertical asymptote at \(x=\dfrac{5}{2}\).
To determine the behavior to the right of \(x=\dfrac{5}{2}\), we find the right-hand limit. \begin{equation*} \lim\limits_{x\rightarrow \frac{5}{2}^{+}}R(x)=\lim\limits_{x\rightarrow \frac{5}{2}^{+}}\left[ \frac{3(x+2)}{(2x-5)}\right] = 3\lim\limits_{x\rightarrow \frac{5}{2}^{+}}\frac{x+2}{2x-5}=\infty \end{equation*}
As \(x\) approaches \(\dfrac{5}{2}\) from the right, the graph of \(R\) becomes unbounded in the positive direction.
Next we consider \(\lim\limits_{x\rightarrow 2}R(x)\). \begin{equation*} \lim\limits_{x\rightarrow 2}R(x)=\lim\limits_{x\rightarrow 2}\frac{ 3(x-2)(x+2)}{(2x-5)(x-2)}=\lim\limits_{x\rightarrow 2}\frac{3(x+2)}{2x-5}= \frac{3(2+2)}{2\cdot 2-5}=\frac{12}{-1}=-12 \end{equation*}
The function \(R\) does not have a vertical asymptote at \(2.\)
Since \(2\) is not in the domain of \(R,\) the graph of \(R\) has a hole at the point \((2,-12)\).

To check for horizontal asymptotes, we find the limits at infinity. \[ \begin{eqnarray*} \lim_{x\rightarrow \infty }R( x) &=&\lim_{x\rightarrow \infty } \frac{3x^{2}-12}{2x^{2}-9x+10}\underset{\underset{\underset{\color{#0066A7}{\hbox{and denominator by \(2x^{2}\)}}}{\color{#0066A7}{\hbox{Divide the numerator}}}}{\color{#0066A7}{\uparrow}}} {=} \lim_{x\rightarrow \infty }\frac{\dfrac{3}{2}-\dfrac{6}{x^{2}}}{1-\dfrac{9}{ 2x}+\dfrac{5}{x^{2}}}=\frac{\lim\limits_{x\rightarrow \infty }\left( \dfrac{3 }{2}-\dfrac{6}{x^{2}}\right) }{\lim\limits_{x\rightarrow \infty }\left( 1- \dfrac{9}{2x}+\dfrac{5}{x^{2}}\right) }\\ &=&\dfrac{\dfrac{3}{2}-0}{1-0+0}=\frac{3 }{2} \\ \end{eqnarray*} \]
127
\[ \begin{eqnarray*} \lim_{x\rightarrow \infty }R( x) &=&\lim_{x\rightarrow \infty } \frac{3x^{2}-12}{2x^{2}-9x+10}\underset{\underset{\underset{\color{#0066A7}{\hbox{and denominator by \(2x^{2}\)}}}{\color{#0066A7}{\hbox{Divide the numerator}}}}{\color{#0066A7}{\uparrow}}} {=} \lim_{x\rightarrow \infty }\frac{\dfrac{3}{2}-\dfrac{6}{x^{2}}}{1-\dfrac{9}{ 2x}+\dfrac{5}{x^{2}}}\\ &=&\frac{\lim\limits_{x\rightarrow \infty }\left( \dfrac{3 }{2}-\dfrac{6}{x^{2}}\right) }{\lim\limits_{x\rightarrow \infty }\left( 1- \dfrac{9}{2x}+\dfrac{5}{x^{2}}\right) }=\frac{3 }{2} \end{eqnarray*} \]
The line \(y=\dfrac{3}{2}\) is a horizontal asymptote of the graph of \(R\) for \(x\) unbounded in the negative direction and for \(x\) unbounded in the positive direction.
The graph of \(R\) and its asymptotes is shown in Figure 63. Notice the hole at the point \((2,-12)\).
NOW WORK
Problem 69.