1.5 Assess Your Understanding
Concepts and Vocabulary
Question
True or False \(\infty \) is a number.
Question
- \(\lim\limits_{x\rightarrow 0^{-}}\dfrac{1}{x}=\) _____;
- \(\lim\limits_{x\rightarrow 0^{+}}\dfrac{1}{x}=\) _____;
- \(\lim\limits_{x\rightarrow 0^{+}}\ln x=\) _____;
Question
True or False The graph of a rational function has a vertical asymptote at every number \(x\) at which the function is not defined.
Question
If \(\lim\limits_{x\rightarrow 4}f(x)=\infty \), then the line \(x=4\) is a(n)______ asymptote of the graph of \(f.\)
Question
- \(\lim\limits_{x\rightarrow \infty }\dfrac{1}{x}=\)_______;
- \(\lim\limits_{x\rightarrow \infty }\dfrac{1}{x^{2}}=\)_______;
- \(\lim\limits_{x\rightarrow \infty }\ln x=\)_______
Question
True or False \(\lim\limits_{x\rightarrow -\infty }5=0\).
Question
- \(\lim\limits_{x\rightarrow -\infty }e^{x}=\)_______;
- \(\lim\limits_{x\rightarrow \infty }e^{x}=\)_______;
- \(\lim\limits_{x\rightarrow \infty }e^{-x}=\)_______
Question
True or False The graph of a function can have at most two horizontal asymptotes.
Skill Building
In Problems 9–16, use the accompanying graph of \(y=f(x)\).
Question
Find \(\lim\limits_{x\rightarrow \infty }f(x)\).
Question
Find \(\lim\limits_{x\rightarrow -\infty }f(x)\).
Question
Find \(\lim\limits_{x\rightarrow -1^{-}}f(x)\).
Question
Find \(\lim\limits_{x\rightarrow -1^{+}}f(x)\).
Question
Find \(\lim\limits_{x\rightarrow 3^{-}}f(x)\).
Question
Find \(\lim\limits_{x\rightarrow 3^{+}}f(x)\).
Question
Identify all vertical asymptotes.
Question
Identify all horizontal asymptotes.

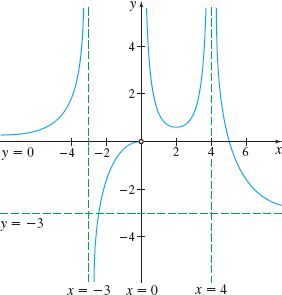
In Problems 17–26, use the accompanying graph of \(y=f(x)\).
Question
Find \(\lim\limits_{x\rightarrow \infty }f(x)\).
Question
Find \(\lim\limits_{x\rightarrow -\infty }f(x)\)
Question
Find \(\lim\limits_{x\rightarrow -3^{-}}f(x)\).
Question
Find \(\lim\limits_{x\rightarrow -3^{+}}f(x)\).
Question
Find \(\lim\limits_{x\rightarrow 0^{-}}f(x)\).
Question
Find \(\lim\limits_{x\rightarrow 0^{+}}f(x)\).
Question
Find \(\lim\limits_{x\rightarrow 4^{-}}f(x)\).
Question
Find \(\lim\limits_{x\rightarrow 4^{+}}f(x)\).
Question
Identify all vertical asymptotes.
Question
Identify all horizontal asymptotes.
In Problems 27–42, find each limit.
Question
\(\lim\limits_{x\rightarrow 2^{-}}\dfrac{3x}{x-2}\)
Question
\(\lim\limits_{x\rightarrow -4^{+}}\dfrac{2x+1}{x+4}\)
Question
\(\lim\limits_{x\rightarrow 2^{+}}\dfrac{5}{x^{2}-4}\)
Question
\(\lim\limits_{x\rightarrow 1^{-}}\dfrac{2x}{x^{3}-1}\)
Question
\(\lim\limits_{x\rightarrow -1^{+}}\dfrac{5x+3}{x(x+1)}\)
Question
\(\lim\limits_{x\rightarrow 0^{-}}\dfrac{5x+3}{5x(x-1)}\)
Question
\(\lim\limits_{x\rightarrow -3^{-}}\dfrac{1}{x^{2}-9}\)
Question
\(\lim\limits_{x\rightarrow 2^{+}}\dfrac{x}{x^{2}-4}\)
128
Question
\(\lim\limits_{x\rightarrow 3}\dfrac{1-x}{(3-x)^{2}}\)
Question
\(\lim\limits_{x\rightarrow -1}\dfrac{x+2}{(x+1)^{2}}\)
Question
\(\lim\limits_{x\rightarrow \pi ^{-}}\cot x\)
Question
\(\lim\limits_{x\rightarrow -\pi /2^{-}}\tan x\)
Question
\(\lim\limits_{x\rightarrow {\pi }/{2}^{+}}\csc ( 2x)\)
Question
\(\lim\limits_{x\rightarrow -{\pi }/{2}^{-}}\sec x\)
Question
\(\lim\limits_{x\rightarrow -1^{+}}\ln ( x+1)\)
Question
\(\lim\limits_{x\rightarrow 1^{+}}\ln ( x-1) \)
In Problems 43–60, find each limit.
Question
\(\lim\limits_{x\rightarrow \infty }\dfrac{5}{x^{2}+4}\)
Question
\(\lim\limits_{x\rightarrow -\infty }\dfrac{1}{x^{2}-9}\)
Question
\(\lim\limits_{x\rightarrow \infty }\dfrac{2x+4}{5x}\)
Question
\(\lim\limits_{x\rightarrow \infty }\dfrac{x+1}{x}\)
Question
\(\lim\limits_{x\rightarrow \infty }\dfrac{x^{3}+x^{2}+2x-1}{x^{3}+x+1}\)
Question
\(\lim\limits_{x\rightarrow \infty }\dfrac{2x^{2}-5x+2}{5x^{2}+7x-1}\)
Question
\(\lim\limits_{x\rightarrow -\infty }\dfrac{x^{2}+1}{x^{3}-1}\)
Question
\(\lim\limits_{x\rightarrow \infty }\dfrac{x^{2}-2x+1}{x^{3}+5x+4}\)
Question
\(\lim\limits_{x\rightarrow \infty }\left[ \dfrac{3x}{2x+5}-\dfrac{x^{2}+1}{4x^{2}+8}\right]\)
Question
\(\lim\limits_{x\rightarrow \infty }\left[ \dfrac{1}{x^{2}+x+4}-\dfrac{x+1}{3x-1}\right]\)
Question
\(\lim\limits_{x\rightarrow -\infty }\left[ 2e^{x}\left( \dfrac{5x+1}{3x}\right) \right]\)
Question
\(\lim\limits_{x\rightarrow -\infty }\left[ e^{x}\left( \dfrac{x^{2}+x-3}{2x^{3}-x^{2}}\right) \right]\)
Question
\(\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt{x}+2}{3x-4}\)
Question
\(\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt{3x^{3}}+2}{x^{2}+6}\)
Question
\(\lim\limits_{x\rightarrow \infty }\sqrt{\dfrac{3x^{2}-1}{x^{2}+4}}\)
Question
\(\lim\limits_{x\rightarrow \infty }\left( \dfrac{16x^{3}+2x+1}{2x^{3}+3x}\right) ^{2/3}\)
Question
\(\lim\limits_{x\rightarrow -\infty }\dfrac{5x^{3}}{x^{2}+1}\)
Question
\(\lim\limits_{x\rightarrow -\infty }\dfrac{x^{4}}{x-2}\)
In Problems 61–66, find any horizontal or vertical asymptotes of the graph of \(f\).
Question
\(f(x)=3+\dfrac{1}{x}\)
Question
\(f(x)=2-\dfrac{1}{x^{2}}\)
Question
\(f(x)=\dfrac{x^{2}}{x^{2}-1}\)
Question
\(f(x)=\dfrac{2x^{2}-1}{x^{2}-1}\)
Question
\(f( x) =\dfrac{\sqrt{2x^{2}-x+10}}{2x-3}\)
Question
\(f( x) =\dfrac{\sqrt[3]{x^{2}+5x}}{x-6}\)
In Problems 67–72, for each rational function \(R\):
- Find the domain of \(R.\)
- Find any horizontal asymptotes of \(R.\)
- Find any vertical asymptotes of \(R\)
- Discuss the behavior of the graph at numbers where \(R\) is not defined.
Question
\(R( x) =\dfrac{-2x^{2}+1}{2x^{3}+4x^{2}}\)
Question
\(R( x) =\dfrac{x^{3}}{x^{4}-1}\)
Question
\(R( x) =\dfrac{x^{2}+3x-10}{2x^{2}-7x+6}\)
Question
\(R( x) =\dfrac{x( x-1) ^{2}}{( x+3) ^{3}}\)
Question
\(R( x) =\dfrac{x^{3}-1}{x-x^{2}}\)
Question
\(R( x) =\dfrac{4x^{5}}{x^{3}-1}\)
Applications and Extensions
In Problems 73 and 74:
- Sketch a graph of a function \(f\) that has the given properties.
- Define a function that describes the graph.
Question
\(f(3)=0,\quad \lim\limits_{x\rightarrow \infty }f(x)=1\),\(\lim\limits_{x\rightarrow -\infty }f(x)=1\), \(\lim\limits_{x\rightarrow 1^{-}}f(x)=\infty \), \(\lim\limits_{x\rightarrow 1^{+}}f(x)=-\infty \)
Question
\(f(2)=0,\quad \lim\limits_{x\rightarrow \infty }f(x)=0\), \(\lim\limits_{x\rightarrow -\infty }f(x)=0\), \(\lim\limits_{x\rightarrow 0}f(x)=\infty \), \(\lim\limits_{x\rightarrow 5^{-}}f(x)=-\infty \), \(\lim\limits_{x\rightarrow 5^{+}}f(x)=\infty \)
Question
Newton's Law of Cooling Suppose an object is heated to a temperature \(u_0\). Then at time \(t=0\), the object is put into a medium with a constant lower temperature \(T\) causing the object to cool. Newton's Law of Cooling states that the temperature \(u\) of the object at time \(t\) is given by \(u=u(t)=(u_0-T)e^{kt}+T\), where \(k \lt 0\) is a constant.
- Find \(\lim\limits_{t\to \infty}u(t)\). Is this the value you expected? Explain why or why not.
- Find \(\lim\limits_{t\to 0^+}u(t)\). Is this the value you expected? Explain why or why not.
Source: Submitted by the students of Millikin University.
Question
Environment A utility company burns coal to generate electricity. The cost \(C,\) in dollars, of removing \(p\%\) of the pollutants emitted into the air is \begin{equation*} C=\dfrac{70{,}000p}{100-p},\qquad 0\leq p \lt 100\ \end{equation*}
Find the cost of removing:
- 45% of the pollutants,
- 90% of the pollutants.
- Find \(\lim\limits_{p\rightarrow 100^{-}}C\).
- Interpret the answer found in (c).
Question
Pollution Control The cost \(C,\) in thousands of dollars, to remove a pollutant from a lake is \begin{equation*} C( x) =\dfrac{5x}{100-x},\qquad 0\leq x \lt 100\ \end{equation*}
where \(x\) is the percent of pollutant removed. Find \(\lim\limits_{x \rightarrow 100^{-}}C( x) \). Interpret your answer.
Question
Population Model A rare species of insect was discovered in the Amazon Rain Forest. To protect the species, entomologists declared the insect endangered and transferred \(25\) insects to a protected area. The population \(P\) of the new colony \(t\) days after the transfer is \begin{equation*} P( t) =\dfrac{50 ( 1+0.5t) }{2+0.01t}\ \end{equation*}
- What is the projected size of the colony after \(1\) year (365 days)?
- What is the largest population that the protected area can sustain? That is, find \(\lim\limits_{t\rightarrow \infty }P( t).\)
129
 Graph the population \(P\) as a function of time \(t.\)
Graph the population \(P\) as a function of time \(t.\)- Use the graph from (c) to describe the regeneration of the insect population. Does the graph support the answer to (b)?
Question
Population of an Endangered Species Often environmentalists capture several members of an endangered species and transport them to a controlled environment where they can produce offspring and regenerate their population. Suppose six American bald eagles are captured, tagged, transported to Montana, and set free. Based on past experience, the environmentalists expect the population to grow according to the model \begin{equation*} P( t) =\dfrac{500}{1+82.3e^{-0.162t}} \end{equation*}
where \(t\) is measured in years.
- If the model is correct, how many bald eagles can the environment sustain? That is, find \(\lim\limits_{t\rightarrow \infty }P( t) .\)
 Graph the population \(P\) as a function of time \(t.\)
Graph the population \(P\) as a function of time \(t.\)- Use the graph from (b) to describe the growth of the bald eagle population. Does the graph support the answer to (a)?
Question
Hailstones Hailstones typically originate at an altitude of about 3000 meters (m). If a hailstone falls from 3000 m with no air resistance, its speed when it hits the ground would be about 240 meters/second (m/s), which is 540 miles/hour (mi/h)! That would be deadly! But air resistance slows the hailstone considerably. Using a simple model of air resistance, the speed \(v=v( t)\) of a hailstone of mass \(m\) as a function of time \(t\) is given by \(v(t)=\dfrac{mg}{k}(1-e^{-kt/m}) {m}/{\!s}\), where \(g=9.8{m}/{\!s}^{2}\) and \(k\) is a constant that depends on the size of the hailstone, its mass, and the conditions of the air. For a hailstone with a diameter \(d\)= 1 centimeter (cm) and mass \({\rm m}=4.8\times 10^{-4}\) kg, \(k\) has been measured to be \(3.4\times 10^{-4}{kg}/{\!s}\).
- Determine the limiting speed of the hailstone by finding \( \lim\limits_{t\rightarrow \infty }v(t)\). Express your answer in meters per second and miles per hour, using the fact that \(1{mi}/{\!h } \approx 0.447{m}/{\!s}\). This speed is called the terminal speed of the hailstone.
 Graph \(v=v( t)\). Does the graph support the answer to (a)?
Graph \(v=v( t)\). Does the graph support the answer to (a)?
Question
![]() Damped Harmonic Motion The motion of a spring is given by the function \begin{equation*} x( t) =1.2e^{-t/2}\cos t+2.4e^{-t/2}\sin t\ \end{equation*}
Damped Harmonic Motion The motion of a spring is given by the function \begin{equation*} x( t) =1.2e^{-t/2}\cos t+2.4e^{-t/2}\sin t\ \end{equation*}
where \(x\) is the distance in meters from the the equilibrium position and \(t\) is the time in seconds.
- Graph \(y=x( t).\) What is \(\lim\limits_{t \rightarrow \infty }x( t)\), as suggested by the graph?
- Find \(\lim\limits_{t\rightarrow \infty }x( t).\)
- Compare the results of (a) and (b). Is the answer to (b) supported by the graph in (a)?
Question
Decomposition of Chlorine in a Pool Under certain water conditions, the free chlorine (hypochlorous acid, HOCl) in a swimming pool decomposes according to the law of uninhibited decay, \( C=C( t) =C( 0) e^{kt},\) where \(C=C( t)\) is the amount (in parts per million, ppm) of free chlorine present at time \(t\) (in hours) and \(k\) is a negative number that represents the rate of decomposition. After shocking his pool, Ben immediately tested the water and found the concentration of free chlorine to be \(C_{0}=C( 0) =2.5\) ppm. Twenty-four hours later, Ben tested the water again and found the amount of free chlorine to be \(2.2\) ppm.
- What amount of free chlorine will be left after \(72\) hours?
- When the free chlorine reaches \(1.0\) ppm, the pool should be shocked again. How long can Ben go before he must shock the pool again?
- Find \(\lim\limits_{t\rightarrow \infty }C( t)\).
- Interpret the answer found in (c).
Question
Decomposition of Sucrose Reacting with water in an acidic solution at \(35^{\circ}{\rm C},\) the amount \(A\) of sucrose (C\(_{12}\)H\(_{22}\)O\(_{11}\)) decomposes into glucose (C\(_{6}\)H\(_{12}\)O\(_{6}\)) and fructose (C\(_{6}\)H\(_{12}\)O\(_{6}\)) according to the law of uninhibited decay \(A=A( t) =A( 0) e^{kt},\) where \(A=A( t) \) is the amount (in moles) of sucrose present at time \(t\) (in minutes) and \(k\) is a negative number that represents the rate of decomposition. An initial amount \(A_{0}=A( 0)\) = 0.40 mole of sucrose decomposes to 0.36 mole in 30 minutes.
- How much sucrose will remain after 2 hours?
- How long will it take until 0.10 mole of sucrose remains?
- Find \(\lim\limits_{t\rightarrow \infty }A( t).\)
- Interpret the answer found in (c).
Question
Macrophotography A camera lens can be approximated by a thin lens. A thin lens of focal length \(f\) obeys the thin-lens equation \(\dfrac{1 }{f}=\dfrac{1}{p}+\dfrac{1}{q}\), where \(p>f\) is the distance from the lens to the object being photographed and \(q\) is the distance from the lens to the image formed by the lens. See the figure below. To photograph an object, the object's image must be formed on the photo sensors of the camera, which can only occur if \(q\) is positive.

- Is the distance \(q\) of the image from the lens continuous as the distance of the object being photographed approaches the focal length \(f\) of the lens? (Hint: First solve the thin-lens equation for \(q\) and then find \(\lim\limits_{p\rightarrow f^{+}}q.\))
- Use the result from (a) to explain why a camera (or any lens) cannot focus on an object placed close to its focal length.
In Problems 85 and 86, find conditions on \(a,b,c\), and \(d\) so that the graph of \(f\) has no horizontal or vertical asymptotes.
Question
\(f(x)=\dfrac{ax^{3}+b}{cx^{4}+d}\)
Question
\(f(x)=\dfrac{ax+b}{cx+d}\)
Question
Explain why the following properties are true. Give an example of each.
130
- If \(n\) is an even positive integer, then \(\lim\limits_{x\rightarrow c} \dfrac{1}{(x-c)^{n}}=\infty \).
- If \(n\) is an odd positive integer, then \(\lim\limits_{x\rightarrow c^{-}}\dfrac{1}{(x-c)^{n}}=-\infty \).
- If \(n\) is an odd positive integer, then \(\lim\limits_{x\rightarrow c^{+}}\dfrac{1}{(x-c)^{n}}=\infty\).
Question
Explain why a rational function, whose numerator and denominator have no common zeros, will have vertical asymptotes at each point of discontinuity.
Question
Explain why a polynomial function of degree \(1\) or higher cannot have any asymptotes.
Question
If \(P\) and \(Q\) are polynomials of degree \(m\) and \(n\), respectively, discuss \(\lim\limits_{x\rightarrow \infty }\dfrac{P(x)}{ Q( x) }\) when:
- \(m \gt n\)
- \(m = n\)
- \(m \lt n\)
Question
 Use a table to investigate \(\lim\limits_{x \rightarrow \infty }\left( 1+\dfrac{1}{x}\right) ^{\!\!\!x}\).
Use a table to investigate \(\lim\limits_{x \rightarrow \infty }\left( 1+\dfrac{1}{x}\right) ^{\!\!\!x}\). Find \(\lim\limits_{x\rightarrow \infty }\left( 1+ \dfrac{1}{x}\right) ^{\!\!\!x}.\)
Find \(\lim\limits_{x\rightarrow \infty }\left( 1+ \dfrac{1}{x}\right) ^{\!\!\!x}.\)- Compare the results from (a) and (b). Explain the possible causes of any discrepancy.
Challenge Problems
Question
\(\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{x}\right) =1\), but \(\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{x} \right) ^{\!\!\!x}>1\). Discuss why the property \(\lim\limits_{x\rightarrow \infty }[f(x)]^{n}=\left[ \lim\limits_{\kern.5ptx\rightarrow \infty }f(x)\right] ^{n}\) cannot be used to find the second limit.
Question
Kinetic Energy At low speeds the kinetic energy \(K\), that is, the energy due to the motion of an object of mass \(m\) and speed \(v,\) is given by the formula \(K=K( v) =\dfrac{1}{2}mv^{2}.\) But this formula is only an approximation to the general formula, and works only for speeds much less than the speed of light, \(c\). The general formula, which holds for all speeds, is \[ K_{\hbox{gen}}( v) =mc^{2}\left[ \dfrac{1}{\sqrt{1-\dfrac{v^{2}}{ c^{2}}}}-1\right] \]
- As an object is accelerated closer and closer to the speed of light, what does its kinetic energy \(K_{\hbox{gen}}\) approach?
- What does the result suggest about the possibility of reaching the speed of light?
