1.2 Limits of Functions Using Properties of Limits

81

OBJECTIVES

When you finish this section, you should be able to:

  1. Find the limit of a sum, a difference, and a product (p. 82)
  2. Find the limit of a power and the limit of a root (p. 84)
  3. Find the limit of a polynomial (p. 86)
  4. Find the limit of a quotient (p. 87)
  5. Find the limit of an average rate of change (p. 89)
  6. Find the limit of a difference quotient (p. 89)

In Section 1.1, we used a numerical approach (tables) and a graphical approach to investigate limits. We saw that these approaches are not always reliable. The only way to be sure a limit is correct is to use the \(\epsilon - \delta\) definition of a limit. In this section, we state without proof results based on the \(\epsilon -\delta\) definition. Some of the results are proved in Section 1.6 and others in Appendix B.

We begin with two basic limits.

THEOREM The Limit of a Constant

If \(f(x)=A,\) where \(A\) is a constant, then for any real number \(c,\) \[ \fbox{\({\lim\limits_{x\rightarrow c}f(x)=\lim\limits_{x\rightarrow c}A=A}\)}\tag{1} \]

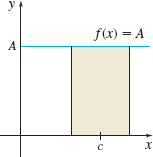
Figure 17 For \(x\) close to \(c\), the value of \(f\) remains at \(A\); \(\lim\limits_{x\to c} A = A\).

The theorem is proved in Section 1.6. See Figure 17 and Table 7 for graphical and numerical support of \(\lim\limits_{x\rightarrow c}A=A\).

Table 7: TABLE 7
\(\underrightarrow{x~\hbox{approaches \(0\) from the left}}\) \(\underleftarrow{x~\hbox{approaches \(0\) from the right}}\)
\(x\) \(c-0.01\) \(c-0.001\) \(c-0.0001\) \(\rightarrow\) \(c\) \(\leftarrow\) \(c+0.0001\) \(c+0.001\) \(c+0.01\)
\(f(x) =A\) \(A\) \(A\) \(A\) \(f(x)\) remains at \(A\) \(A\) \(A\) \(A\)

For example,

\[ \lim_{x\rightarrow 5}2=2\qquad \lim_{x\rightarrow \sqrt{2}}\frac{1}{3}=\frac{ 1}{3}\qquad \lim_{x\rightarrow 5}(-\pi )=-\pi \]

THEOREM The Limit of the Identity Function

If \(f(x)=x\), then for any number \(c\), \[ \fbox{${\lim\limits_{x\rightarrow c}f(x)=\lim\limits_{x\rightarrow c}x=c}$}\tag{2} \]

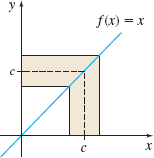
Figure 18 For \(x\) close to \(c\), the value of \(f\) is just as close to \(c\); \(\lim\limits_{x\to c} x = c\).

This theorem is proved in Section 1.6. See Figure 18 and Table 8 for graphical and numerical support of \(\lim\limits_{x\rightarrow c}x=c.\)

Table 8: TABLE 8
\(\underrightarrow{x~\hbox{approaches \(c\) from the left}}\) \(\underleftarrow{x~\hbox{approaches \(c\) from the right}}\)
\(x\) \(c-0.01\) \(c-0.001\) \(c-0.0001\) \(\rightarrow\) \(c\) \(\leftarrow\) \(c+0.0001 \) \(c+0.001\) \(c+0.01\)
\(f(x) = x\) \(c-0.01\) \(c-0.001\) \(c-0.0001\) \(f(x)\) approaches \(c\) \(c+0.0001\) \(c+0.001\) \(c+0.01\)

For example, \[ \lim_{x\rightarrow -5}x=-5\qquad \lim_{x\rightarrow \sqrt{3}}x=\ \sqrt{3} \qquad \lim_{x\rightarrow 0}x=0 \]

1 Find the Limit of a Sum, a Difference, and a Product

82

Many functions are combinations of sums, differences, and products of a constant function and the identity function. The following properties can be used to find the limit of such functions.

IN WORDS

The limit of the sum of two functions equals the sum of their limits.

THEOREM Limit of a Sum

If \(f\) and \(g\) are functions for which \(\lim\limits_{x\rightarrow c} f(x)\) and \(\lim\limits_{x\rightarrow c}g(x)\) both exist, then \(\lim\limits_{x\rightarrow c}[f(x)+g(x)]\) exists and \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow c}[f(x)+g(x)]=\lim\limits_{x\rightarrow c}f(x)+\lim\limits_{x\rightarrow c}g(x)} \]

A proof is given in Appendix B.

Finding the Limit of a Sum

Find \(\lim\limits_{x\rightarrow -3}(x+4)\).

Solution \(F(x)=x+4\) is the sum of two functions \(f(x)=x\) and \( g(x)=4\). From the limits given in (1) and (2), we have \[ \begin{equation*} \lim_{x\rightarrow -3}f(x)=\lim_{x\rightarrow -3}x=-3\qquad \hbox{and}\qquad \lim_{x\rightarrow -3}g(x)=\lim_{x\rightarrow -3}4=4 \end{equation*} \]

Then, using the Limit of a Sum, we have \[ \begin{equation*} \lim_{x\rightarrow -3}(x+4)=\lim_{x\rightarrow -3}x+\lim_{x\rightarrow -3}4=-3+4=1 \end{equation*} \]

IN WORDS

The limit of the difference of two functions equals the difference of their limits.

THEOREM Limit of a Difference

If \(f\) and \(g\) are functions for which \(\lim\limits_{x\rightarrow c}f( x)\) and \(\lim\limits_{x\rightarrow c}g(x)\) both exist, then \(\lim\limits_{x\rightarrow c}[f(x)-g(x)]\) exists and \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow c}[f(x)-g(x)]=\lim\limits_{x\rightarrow c}f(x)-\lim\limits_{x\rightarrow c}g(x)} \]

Finding the Limit of a Difference

Find \(\lim\limits_{x\rightarrow 4} (6-x)\).

Solution \(F(x)=6-x\) is the difference of two functions \(f(x)=6\) and \(g(x)=x\). \[ \lim_{x\rightarrow 4}f(x)=\lim_{x\rightarrow 4}6=6\qquad \hbox{and}\qquad \lim_{x\rightarrow 4}g(x)=\lim_{x\rightarrow 4}x=4 \]

Then, using the Limit of a Difference, we have \[ \begin{equation*} \lim_{x\rightarrow 4}(6-x)=\lim_{x\rightarrow 4}6-\lim_{x\rightarrow 4}x=6-4=2 \end{equation*} \]

IN WORDS

The limit of the product of two functions equals the product of their limits.

THEOREM Limit of a Product

If \(f\) and \(g\) are functions for which \(\lim\limits_{x\rightarrow c}f( x) \) and \(\lim\limits_{x\rightarrow c}g(x)\) both exist, then \(\lim\limits_{x\rightarrow c}[f(x)\cdot g(x)]\) exists and \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow c}[f(x)\cdot g(x)]=\lim\limits_{x\rightarrow c}f(x)\cdot \lim\limits_{x\rightarrow c}g(x)} \]

A proof is given in Appendix B.

83

Finding the Limit of a Product

Find:

  1. \(\lim\limits_{x\rightarrow 3}x^{2}\)
  2. \(\lim\limits_{x\rightarrow -5}(-4x)\)

Solution

  1. \(F( x) =x^{2}\) is the product of two functions, \(f(x)=x\) and \(g(x)=x\). Then, using the Limit of a Product, we have \[ \lim_{x\rightarrow 3}x^{2}=\lim_{x\rightarrow 3}x\cdot \lim_{x\rightarrow 3}x=(3)(3)=9\]
  2. \(F(x)=-4x\) is the product of two functions, \(f(x)=-4\) and \( g(x)=x\). Then, using the Limit of a Product, we have \[ \lim\limits_{x\rightarrow -5}(-4x)=\lim_{x\rightarrow -5}(-4)\cdot \lim\limits_{x\rightarrow -5}x=(-4)(-5)=20\]

A corollary* of the Limit of a Product Theorem is the special case when \(f(x)=k\) is a constant function.

*A corollary is a theorem that follows directly from a previously proved theorem.

IN WORDS

The limit of a constant times a function equals the constant times the limit of the function.

COROLLARY Limit of a Constant Times a Function

If \(g\) is a function for which \(\lim\limits_{x\rightarrow c}g(x)\) exists and if \(k\) is any real number, then \(\lim\limits_{x\rightarrow c}[kg(x)]\) exists and \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow c} [kg(x)]=k\lim\limits_{x\rightarrow c} g(x)} \]

You are asked to prove this corollary in Problem 103.

Limit properties often are used in combination.

Finding a Limit

Find:

  1. \(\lim\limits_{x\rightarrow 1}[2x(x+4)]\)
  2. \(\lim\limits_{x\rightarrow 2^{+}}[4x(2-x)]\)

Solution

NOTE

The limit properties are also true for one-sided limits.

  1. \[ \begin{array}{rcl@{\qquad}l} \lim\limits_{x\rightarrow 1}[(2x)(x+4)] &=&\left[ \lim\limits_{\kern.5ptx\rightarrow 1}(2x)\right] \left[ \lim\limits_{\kern.5ptx\rightarrow 1}(x+4)\right] &{\color{#0066A7}{\hbox{Limit of a Product}}}\\ &=&\left[ 2\cdot \lim\limits_{x\rightarrow 1}x\right] \cdot \left[ \lim\limits_{\kern.5ptx\rightarrow 1}x+\lim\limits_{x\rightarrow 1}4\right] &{\color{#0066A7}{\hbox{Limit of a Constant Times a Function, Limit of a Sum}}}\\ &=&(2\cdot 1)\cdot (1+4)=10 & {\color{#0066A7}{\hbox{Use (2) and (1), and simplify.}}} \end{array} \]
  2. We use properties of limits to find the one-sided limit. \[ \begin{eqnarray*} \lim \limits_{x\rightarrow 2^{+}}[4x(2-x)] &=& 4\lim \limits_{x\rightarrow 2^{+}} [ x( 2-x) ] =4 \Big[ \lim \limits_{x\rightarrow 2^{+}}x \Big ]~ \Big[ \lim \limits_{x\rightarrow 2^{+}}( 2-x) \Big ]\\ &=& 4 \cdot 2 \Big[ \lim \limits_{x \rightarrow 2^{+}}2 - \lim \limits_{x \rightarrow 2^{+}}x \Big ] = 4 \cdot 2 \cdot (2 - 2) = 0 \end{eqnarray*} \]

NOW WORK

Problem 13.

To find the limit of piecewise-defined functions at numbers where the defining equation changes requires the use of one-sided limits.

84

RECALL

The limit \(L\) of a function \(y=f(x)\) as \(x\) approaches a number \(c\) exists if and only if \(\lim\limits_{x\rightarrow c^{-}}{f}(x)=\lim\limits_{x\rightarrow c^{+}}{f}(x)=L\).

Finding a Limit

Find \(\lim\limits_{x\rightarrow 2} f(x)\), if it exists, if \[ f( x) =\left\{ \begin{array}{l@{\qquad}ll} 3x+1 & \hbox{if }\quad x\lt 2 \\[3pt] 2x( x-1) & \hbox{if }\quad x\geq 2 \end{array} \right. \]

Figure 19 \[ f( x) =\left\{ \begin{array}{l@{\qquad}ll} 3x+1 & \hbox{if } x\lt 2 \\[3pt] 2x( x-1) & \hbox{if } x\geq 2 \end{array} \right. \]

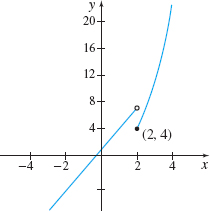
Solution Since the rule for \(f\) changes at \(2,\) we need to find the one-sided limits of \(f\) as \(x\) approaches \(2\).

For \(x\lt 2,\) we use the left-hand limit. \begin{equation*} \lim\limits_{x\rightarrow 2^{-}}f(x) =\lim\limits_{x\rightarrow 2^{-}}(3x+1) =\lim\limits_{x\rightarrow 2^{-}}(3x) +\lim\limits_{x\rightarrow 2^{-}}1=3\!\lim\limits_{x\rightarrow 2^{-}}x+1=3(2) +1=7 \end{equation*}

For \(x>2,\) we use the right-hand limit. \begin{eqnarray*} \lim\limits_{x\rightarrow 2^{+}}f(x) &=&\lim\limits_{x\rightarrow 2^{+}}[ 2x(x-1)] =\lim\limits_{x\rightarrow 2^{+}}(2x) \cdot \lim\limits_{x\rightarrow 2^{+}}(x-1)\\[4pt] &=&2\lim\limits_{x\rightarrow 2^{+}}x\cdot \Big[ \lim\limits_{x\rightarrow 2^{+}}x-\lim\limits_{x\rightarrow 2^{+}}1\Big] =2\cdot 2\,[2-1] =4 \end{eqnarray*}

Since \(\lim\limits_{x\rightarrow 2^{-}}f(x) =7\neq \lim\limits_{x\rightarrow 2^{+}}f(x) =4,\) \(\lim\limits_{x \rightarrow 2}f(x) \) does not exist.

See Figure 19.

NOW WORK

Problem 73.

The Heaviside function, \(u_{c}( t) =\left\{ \begin{array}{l@{\qquad}l} 0 & \hbox{if }t\lt c \\ 1 & \hbox{if }t\geq c \end{array}\right.\), is a step function that is used in electrical engineering to model a switch. The switch is off if \(t \lt c\), and it is on if \(t\geq c.\)

Finding a Limit of the Heaviside Function

ORIGINS

Oliver Heaviside (1850–1925) was a self-taught mathematician and electrical engineer. He developed a branch of mathematics called operational calculus in which differential equations are solved by converting them to algebraic equations. Heaviside applied vector calculus to electrical engineering and, perhaps most significantly, he simplified Maxwell's equations to the form used by electrical engineers to this day. In 1902 Heaviside claimed there is a layer surrounding Earth from which radio signals bounce, allowing the signals to travel around the Earth. Heaviside's claim was proved true in 1923. The layer, contained in the ionosphere, is named the Heaviside layer. The function we discuss here is one of his minor contributions to mathematics and electrical engineering.

Find \(\lim\limits_{t\rightarrow 0}u_{0}(t) ,\) where \(u_{0}(t) =\left\{ \begin{array}{l@{\quad}ll} 0 & \hbox{if} & t\lt 0 \\ 1 & \hbox{if} & t\geq 0 \end{array} \right. \)

Solution Since this Heaviside function changes rules at \(t=0\), we find the one-sided limits as \(t\) approaches \(0\). \[ \hbox{For \(t\lt 0\), \(\lim\limits_{t\rightarrow 0^{-}}u_{0}(t) =\lim\limits_{t\rightarrow 0^{-}}0=0\) and for \(t\geq 0\), \(\lim\limits_{t\rightarrow 0^{+}} u_{0}( t) =\lim\limits_{t\rightarrow 0^{+}} 1=1\)} \]

Since the one-sided limits as \(t\) approaches \(0\) are not equal, \(\lim\limits_{t\rightarrow 0}\) \(u_{0}(t) \) does not exist.

NOW WORK

Problem 81.

2 Find the Limit of a Power and the Limit of a Root

Using the Limit of a Product, if \(\lim\limits_{x\rightarrow c}f(x) \) exists, then \[ \lim\limits_{x\rightarrow c}[f(x)]^{2}=\lim\limits_{x\rightarrow c}[f(x)\cdot f(x) ]=\lim\limits_{x\rightarrow c}f(x)\cdot \lim\limits_{x\rightarrow c}f(x)=\Big[ \lim\limits_{x\rightarrow c}f(x)\Big] ^{2} \]

Repeated use of this property produces the next corollary.

COROLLARY Limit of a Power

If \(\lim\limits_{x\rightarrow c}f(x)\) exists and if \(n\geq 2\) is an integer, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow c}[f(x)]^{n}=\Big[ \lim\limits_{x\rightarrow c}f(x)\Big] ^{n}} \]

85

Finding the Limit of a Power

Find:

  1. \(\lim\limits_{x\rightarrow 2}x^{5}\)
  2. \(\lim\limits_{x\rightarrow 1}( 2x-3) ^{3}\)
  3. \(\lim\limits_{x\rightarrow c}x^{n}\)

Solution

  1. \(\lim\limits_{x\rightarrow 2} x^{5}=\left( \lim\limits_{\kern.5ptx\rightarrow 2}x\right) ^{5}=2^{5}=32\)
  2. \(\lim\limits_{x\rightarrow 1}( 2x-3) ^{3}=\) \(\left[ \lim\limits_{\kern.5ptx\rightarrow 1}( 2x-3) \right] ^{3}=\) \(\left[ \lim\limits_{\kern.5ptx\rightarrow 1}( 2x) -\lim\limits_{x\rightarrow 1}3 \right] ^{3}\ =( 2 -3) ^{3}=-1\)
  3. \(\lim\limits_{x\rightarrow c}x^{n}=\left[ \lim\limits_{\kern.5ptx\rightarrow c}x\right] ^{n}=c^{n}\)

The result from Example 7(c) is worth remembering since it is used frequently: \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{x\rightarrow c}x^{n}=c^{n}}\]

where \(c\) is a number and \(n\) is a positive integer.

NOW WORK

Problem 15.

THEOREM Limit of a Root

If \(\lim\limits_{x\rightarrow c}f(x)\) exists and if \(n\geq 2\) is an integer, then \[\bbox[5px, border:1px solid black, #F9F7ED] {\lim\limits_{x\rightarrow c}\sqrt[n]{ f(x)}=\sqrt[n]{\lim\limits_{x\rightarrow c}f(x)}} \] provided \(f(x)\geq 0\) if \(n\) is even.

Finding the Limit of \(f(x)=\ \sqrt[3]{x^2+11}\)

Find \(\lim\limits_{x\rightarrow 4}\ \sqrt[3]{x^{2}+11}\).

Solution \begin{eqnarray*} \lim\limits_{x\rightarrow 4}\sqrt[3]{x^{2}+11}\underset{\underset{\color{#0066A7}{\hbox{Limit of a Root}}}{\color{#0066A7}{\uparrow}}}{=}\sqrt[3]{\lim\limits_{x\rightarrow 4}(x^{2}+11)} \underset{\underset{\color{#0066A7}{\hbox{Limit of a Sum}}}{\color{#0066A7}{\uparrow}}}{=}\sqrt[3]{\lim\limits_{x\rightarrow 4}x^{2}+\lim\limits_{x\rightarrow 4}11}\\ \underset{\underset{\color{#0066A7}{\hbox{\(\lim\limits_{x\rightarrow c}x^2=c^2\)}}}{\color{#0066A7}{\uparrow}}}{=} \sqrt[3]{4^{2}+11} =\sqrt[3]{27}=3 \\[-14pt] \end{eqnarray*}

NOW WORK

Problem 19.

The Limit of a Power and the Limit of a Root are used together to find the limit of a function with a rational exponent.

THEOREM Limit of \([f( x)] ^{m/n}\)

If \(f\) is a function for which \(\lim\limits_{x\rightarrow c}f( x) \) exists and if \([f( x)] ^{m/n}\) is defined for positive integers \(m\) and \(n\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{ \lim\limits_{x\rightarrow c}[f(x)]^{m/n}= \left[ \lim\limits_{\kern.5ptx\rightarrow c}f(x)\right] ^{m/n}} \]

86

Figure 20 \(f(x)=(x+1)^{3/2}\)

Finding the Limit of \({f(x)=(x+1)^{3/2}}\)

Find \(\lim\limits_{x\rightarrow 8}(x+1)^{3/2}\).

Solution Let \(f(x)=x+1\). Near \(8,\) \(x+1>0,\) so \(( x+1) ^{3/2}\) is defined. Then \[ \begin{eqnarray*} \lim\limits_{x\rightarrow 8}[f(x)]^{3/2}&=&\lim\limits_{x\rightarrow 8}(x+1)^{3/2}\underset{\underset{\color{#0066A7}{\hbox{\(\begin{array}{c}{\lim\limits_{x\rightarrow c}{[f(x)]}^{m/n}{=} \left[ \lim\limits_{\kern.5ptx\rightarrow c}{f(x)}\right]^{m/n}}\end{array}\)}}}{\color{#0066A7}{\uparrow}}}{=}\left[ \lim\limits_{\kern.5ptx\rightarrow 8}(x+1)\right] ^{3/2}=[8+1]^{3/2}=9^{3/2}=27 \end{eqnarray*} \]

See Figure 20.

NOW WORK

Problem 23.

3 Find the Limit of a Polynomial

Some limits can be found by substituting \(c\) for \(x.\) For example, \[ \lim\limits_{x\rightarrow 2}(5x^{2})=5\lim\limits_{x\rightarrow 2}x^{2}=5\cdot 2^{2}=20. \]

Since \(\lim\limits_{x\rightarrow c}x^{n}=c^{n}\) if \(n\) is a positive integer, we can use the Limit of a Constant Times a Function to obtain a formula for the limit of a monomial \(f(x)=ax^{n}\). \[\bbox[5px, border:1px solid black, #F9F7ED]{ \lim\limits_{x\rightarrow c}(ax^{n})=ac^{n}} \]

where \(a\) is any number.

Since a polynomial is the sum of monomials and the limit of a sum is the sum of the limits, we have the following result.

IN WORDS

To find the limit of a polynomial as \({x}\) approaches \(c\), evaluate the polynomial at \({c}\).

THEOREM Limit of a Polynomial Function

If \(P\) is a polynomial function, then \[\bbox[5px, border:1px solid black, #F9F7ED] {\lim\limits_{x\rightarrow c}P(x)=P(c)} \] for any number \(c\).

Proof

If \(P\) is a polynomial function, that is, if \[ \begin{equation*} P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0} \end{equation*} \]

where \(n\) is a nonnegative integer, then \[ \begin{eqnarray*} \lim_{x\rightarrow c}P(x) &=&\lim_{x\rightarrow c}\big(a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}\big) \nonumber \\[2pt] &=&\lim\limits_{x\rightarrow c}\big(a_{n}x^{n}\big)+\lim\limits_{x\rightarrow c}\big(a_{n-1}x^{n-1}\big)+\cdots +\lim\limits_{x\rightarrow c}(a_{1}x)+\lim\limits_{x\rightarrow c}a_{0}\\[2pt] &=&a_{n}c^{n}+a_{n-1}c^{n-1}+\cdots +a_{1}c+a_{0}\qquad\qquad {\color{#0066A7}{\hbox{Limit of a Monomial}}} \\ &=&P(c) \end{eqnarray*} \]

Finding the Limit of a Polynomial

Find the limit of each polynomial:

  1. \(\lim\limits_{x\rightarrow 3}(4x^{2}-x+2)=4( 3) ^{2}-3+2=35\)
  2. \(\lim\limits_{x\rightarrow -1}(7x^{5}+4x^{3}-2x^{2})=7(-1)^{5}+4(-1)^{3}-2(-1)^{2}=-13\)
  3. \(\lim\limits_{x\rightarrow 0}(10x^{6}-4x^{5}-8x+5)=10(0)^{6}-4(0)^{5}-8(0)+5=5\)

NOW WORK

Problem 29.

4 Find the Limit of a Quotient

87

To find the limit of a rational function, which is the quotient of two polynomials, we use the following result.

IN WORDS

The limit of the quotient of two functions equals the quotient of their limits, provided that the limit of the denominator is not zero.

THEOREM Limit of a Quotient

If \(f\) and \(g\) are functions for which \(\lim\limits_{x\rightarrow c}f( x) \) and \(\lim\limits_{x\rightarrow c}g(x)\) both exist, then \(\lim\limits_{x\rightarrow c}\left[ \dfrac{f( x) }{g( x) }\right] \) exists and \[{\lim\limits_{x\rightarrow c}\left[ \dfrac{ f(x)}{g(x)}\right] =\dfrac{\lim\limits_{x\rightarrow c}f(x)}{\lim\limits_{x\rightarrow c}g(x)}}\]

provided \(\lim\limits_{x\rightarrow c}g(x)\neq 0\).

NEED TO REVIEW

Rational functions are discussed in Section P.2, pp. 19-20.

COROLLARY Limit of a Rational Function

If the number \(c\) is in the domain of a rational function \(R( x) =\) \(\dfrac{p(x)}{q(x)}\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{ \lim\limits_{x\rightarrow c}R(x)=R(c)}\tag{3} \]

You are asked to prove this corollary in Problem 104.

Finding the Limit of a Rational Function

Find:

  1. \(\lim\limits_{x\rightarrow 1}\dfrac{3x^{3}-2x+1}{4x^{2}+5}\)
  2. \(\lim\limits_{x\rightarrow -2}\dfrac{2x+4}{3x^{2}-1}\)

Solution

  1. Since \(1\) is in the domain of the rational function \(R( x) =\dfrac{3x^{3}-2x+1}{4x^{2}+5},\) \[ \begin{equation*} \lim_{x\rightarrow 1}R( x) \underset{\underset{\color{#0066A7}{\hbox{Use (3)}}}{\color{#0066A7}{\uparrow}}}{=}R( 1) =\frac{3-2+1}{4+5}=\frac{2}{9} \end{equation*} \]
  2. Since \(-2\) is in the domain of the rational function \(H(x) =\dfrac{2x+4}{3x^{2}-1}\), \[ \begin{equation*} \lim_{x\rightarrow -2}H( x) \underset{\underset{\color{#0066A7}{\hbox{Use (3)}}}{\color{#0066A7}{\uparrow}}}{=}H( -2) =\frac{-4+4}{12-1}=\dfrac{0}{11}=0 \end{equation*} \]

NOW WORK

Problem 33.

Finding the Limit of a Quotient

Find \(\lim\limits_{x\rightarrow 4}\dfrac{\sqrt{3x^{2}+1}}{x-1}\).

Solution We seek the limit of the quotient of two functions. Since the limit of the denominator \(\lim\limits_{x\rightarrow 4}(x-1)\neq 0\) , we use the Limit of a Quotient. \[ \begin{eqnarray*} \lim_{x\rightarrow 4}\frac{\sqrt{3x^{2}+1}}{x-1}\underset{\underset{\color{#0066A7}{\hbox{Limit of a Quotient}}}{\color{#0066A7}{\uparrow}}}{=}\frac{\lim\limits_{x\rightarrow 4}\sqrt{ 3x^{2}+1}}{\lim\limits_{x\rightarrow 4}(x-1)}\underset{\underset{\color{#0066A7}{\hbox{Limit of a Root}}}{\color{#0066A7}{\uparrow}}}{=}\frac{\sqrt{\lim\limits_{x\rightarrow 4} (3x^{2}+1)}}{\lim\limits_{x\rightarrow 4}(x-1)}=\frac{\sqrt{3\cdot 4^{2}+1}}{4-1}=\frac{\sqrt{49}}{3}=\frac{7}{3}\\[-13pt] \end{eqnarray*}\]

NOW WORK

Problem 31.

88

Based on these examples, you might be tempted to conclude that finding a limit as \(x\) approaches \(c\) is simply a matter of substituting the number \(c\) into the function. The next few examples show that substitution cannot always be used and other strategies need to be employed.

The limit of a rational function can be found using substitution, provided the number \(c\) being approached is in the domain of the rational function. The next example shows a strategy that can be tried when \(c\) is not in the domain.

Finding the Limit of a Rational Function

Find \(\lim\limits_{x\rightarrow -2}\dfrac{x^{2}+5x+6}{x^{2}-4}\).

Solution Since \(-2\) is not in the domain of the rational function, (3) cannot be used. But this does not mean that the limit does not exist! Factoring the numerator and the denominator, we find \[ \frac{x^{2}+5x+6}{x^{2}-4}=\frac{(x+2)(x+3)}{(x+2)(x-2)} \]

Since \(x\neq -2\), and we are interested in the limit as \(x\) approaches \(-2\), the factor \(x+2\) can be divided out. Then \[ \begin{eqnarray*} \lim_{x\rightarrow -2}\frac{x^{2}+5x+6}{x^{2}-4}\underset{\underset{\color{#0066A7}{\hbox{Factor}}}{\color{#0066A7}{\uparrow}}}{=}\lim_{x\rightarrow -2}\frac{(x+2)(x+3)}{(x+2)(x-2)} \underset{\underset{\underset{\color{#0066A7}{\hbox{Divide out ( x+2)}}}{\color{#0066A7}{\hbox{x ≠ -2}}}}{\color{#0066A7}{\uparrow}}} {=}\lim_{x\rightarrow -2}\frac{x+3}{x-2} \underset{\underset{\underset{\color{#0066A7}{\hbox{Rational Function}}}{\color{#0066A7}{\hbox{Use the Limit of a}}}}{\color{#0066A7}{\uparrow}}} {=}\dfrac{-2+3}{-2-2}=-\dfrac{1}{4} \end{eqnarray*} \]

NOW WORK

Problem 35.

The Limit of a Quotient property can only be used when the limit of the denominator of the function is not zero. The next example illustrates a strategy to try if radicals are present.

Finding the Limit of a Quotient

Find \(\lim\limits_{x\rightarrow 5}\dfrac{\sqrt{x}-\sqrt{5}}{x-5}\).

Solution The domain of \(h(x)=\dfrac{\sqrt{x}-\sqrt{5}}{x-5}\) is {\({ x|x\geq 0, x\ne 5}\)}. Since the limit of the denominator is \[ \lim\limits_{x\rightarrow 5}g(x)=\lim\limits_{x\rightarrow 5}(x-5)=0 \]

we cannot use the Limit of a Quotient property. A different strategy is necessary. We rationalize the numerator of the quotient. \[ \begin{eqnarray*} \frac{\sqrt{x}-\sqrt{5}}{x-5}&=&\frac{( \sqrt{x}-\sqrt{5}) }{(x-5) }\cdot \frac{( \sqrt{x}+\sqrt{5}) }{( \sqrt{x}+\sqrt{5}) } =\frac{x-5}{(x-5) ( \sqrt{x}+\sqrt{5}) } \underset{\underset{\color{#0066A7}{\hbox{$x\neq 5$}}}{\color{#0066A7}{\uparrow}}}{=} \frac{1}{\sqrt{x}+\sqrt{5}} \end{eqnarray*} \]

Do you see why rationalizing the numerator works? It causes the term \(x-5\) to appear in the numerator, and since \(x\neq 5\), the factor \(x-5\) can be divided out. Then

NOTE

When finding a limit, remember to include “\(\lim\limits_{x\rightarrow c}\)” at each step until you let \({x\rightarrow c}\).

\[ \begin{eqnarray*} \lim_{x\rightarrow 5}\frac{\sqrt{x}-\sqrt{5}}{x-5}&=&\lim_{x\rightarrow 5}\frac{1}{\sqrt{x}+\sqrt{5}} \underset{\underset{\color{#0066A7}{\hbox{Use the Limit of a Quotient}}}{\color{#0066A7}{\uparrow}}} {=}\frac{1 }{\sqrt{5}+\sqrt{5}}=\frac{1}{2\sqrt{5}}=\frac{\sqrt{5}}{10} \end{eqnarray*} \]

NOW WORK

Problem 41.

5 Find the Limit of an Average Rate of Change

89

The next two examples illustrate limits that we encounter in Chapter 2.

NEED TO REVIEW?

Average rate of change is discussed in Section P.1, p. 11.

In Section P.1, we defined average rate of change: If \(a\) and \(b\), where \(a\neq b\), are in the domain of a function \(y=f(x)\), the average rate of change of \(f\) from \(a\) to \(b\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{\Delta y}{\Delta x}=\dfrac{f( b) -f( a) }{b-a}\qquad a\neq b } \]

Finding the Limit of an Average Rate of Change

  1. Find the average rate of change of \(f( x) =x^{2}+3x\) from \(2\) to \(x;\) \(x\neq 2\).
  2. Find the limit as \(x\) approaches \(2\) of the average rate of change of \(f( x) =x^{2}+3x\) from \(2\) to \(x\).

Solution (a) The average rate of change of \(f\) from \(2\) to \(x\) is \[ \begin{equation*} \dfrac{\Delta y}{\Delta x}=\frac{f(x)-f(2)}{x-2}=\frac{(x^{2}+3x)- [ 2^{2}+3( 2)] }{x-2}=\frac{x^{2}+3x-10}{x-2}=\frac{(x+5)(x-2)}{x-2} \end{equation*} \]

(b) The limit of the average rate of change is \[ \begin{equation*} \lim_{x\rightarrow 2}\frac{f(x)-f(2)}{x-2}=\lim_{x\rightarrow 2}\frac{ (x+5)(x-2)}{x-2}=\lim_{x\rightarrow 2}( x+5) =7 \end{equation*} \]

NOW WORK

Problem 63.

6 Find the Limit of a Difference Quotient

In Section P.1, we defined the difference quotient for a function \(f\) as \[ \dfrac{f( x+h) -f( x) }{h}, h\neq 0. \]

Finding the Limit of a Difference Quotient

  1. For \(f(x)=2x^{2}-3x+1\), find the difference quotient \(\dfrac{f(x+h)-f(x)}{h}\), \(h\neq 0\).
  2. Find the limit as \(h\) approaches \(0\) of the difference quotient of \(f( x) =2x^{2}-3x+1\).

Solution (a) To find the difference quotient of \(f\), we begin with \(f( x+h) \). \[ \begin{eqnarray*} f(x+h)&=&2(x+h)^{2}-3(x+h)+1=2( x^{2}+2xh+h^{2}) -3x-3h+1\\[4pt] &=&2x^{2}+4xh+2h^{2}-3x-3h+1 \end{eqnarray*} \]

Now \begin{equation*} f( x+h) -f( x) = ( 2x^{2}+4xh+2h^{2}-3x-3h+1 ) - ( 2x^{2}-3x+1 ) =4xh+2h^{2}-3h \end{equation*}

Then, the difference quotient is \begin{equation*} \dfrac{f(x+h)-f(x)}{h}=\frac{4xh+2h^{2}-3h}{h}=\frac{h(4x+2h-3)}{h}=4x+2h-3, \hbox{ }h\neq 0 \end{equation*}

(b) \(\lim\limits_{h\rightarrow 0}\dfrac{f(x+h)-f(x)}{h} =\lim\limits_{h\rightarrow 0}( 4x+2h-3) =4x+0-3=4x-3\)

NOW WORK

Problem 71.

90

Summary

Two Basic Limits

Properties of Limits

If \(f\) and \(g\) are functions for which \(\lim\limits_{x\rightarrow c}f( x)\) and \(\lim\limits_{x\rightarrow c}g(x)\) both exist, and \(k\) is a constant, then