1.2 Assess Your Understanding

Printed Page 90

Concepts and Vocabulary

    1. (a) \(\lim\limits_{x\rightarrow 4}\,(-3)=\)_____;
    2. (b) \(\lim\limits_{x\rightarrow 0}\pi =\) _____

  1. (a) \(-3\)
  2. (b) \(\pi \)

  1. \(\lim\limits_{x\rightarrow c}f(x)=3\), then \(\lim\limits_{x\rightarrow c}[f(x)]^{5}=\) _____.

243

  1. If \(\lim\limits_{x\rightarrow c}f(x)=64\), then \(\lim\limits_{x\rightarrow c}\sqrt[3]{f(x)}=\) _____.

4

    1. (a) \(\lim\limits_{x\rightarrow -1}x\) = _____;
    2. (b) \(\lim\limits_{x\rightarrow e}x=\) _____

  1. (a) \(-1\)
  2. (b) \(e\)
    1. (a) \(\lim\limits_{x\rightarrow 0}\,( x-2)\) = _____;
    2. (b) \(\lim\limits_{x\rightarrow {1}/{2}} (3+x)\) =_____

  1. (a) \(-2\)
  2. (b) \(\dfrac{7}{2}\)
    1. (a) \(\lim\limits_{x\rightarrow 2}\, ( -3x)\) = _____;
    2. (b) \(\lim\limits_{x\rightarrow 0}\, ( 3x)\) = _____

  1. (a) \(-6\)
  2. (b) 0

  1. True or False If \(p\) is a polynomial function, then \(\lim\limits_{x\rightarrow 5}p( x) =p(5) \).

True

  1. If the domain of a rational function \(R\) is \(\{x|\) \(x\neq 0\}\), then \(\lim\limits_{x\rightarrow 2}R(x)=R\) (_____).

2

  1. True or False Properties of limits cannot be used for one-sided limits.

False

  1. True or False If \(f(x)=\dfrac{( x+1) ( x+2) }{x+1}\) and \(g(x)=x+2\), then \(\lim\limits_{x\rightarrow -1}f(x)=\lim\limits_{x\rightarrow -1}g(x)\).

True

Skill Building

In Problems 11-44, find each limit using properties of limits.

  1. \({\lim\limits_{x\rightarrow 3}}\, [ 2({x+4})]\)

14

  1. \({\lim\limits_{x\rightarrow -2}} [ 3({x+1})]\)

  1. \({\lim\limits_{x\rightarrow -2}}\, [ x ( 3x{-1}) ( {x+2}) ]\)

0

  1. \({\lim\limits_{x\rightarrow -1}} [ x( x-1) ( x+10)] \)

  1. \({\lim\limits_{t\rightarrow 1}}\,( 3t-2) ^{3}\)

1

  1. \({\lim\limits_{x\rightarrow 0}}\,( {-3x+1}) ^{2}\)

  1. \({\lim\limits_{x\rightarrow 4}} \, (3\sqrt{x})\)

6

  1. \({\lim\limits_{x\rightarrow 8}}\left(\dfrac{1}{4}\sqrt[3]{{x}}\right)\)

  1. \({\lim\limits_{x\rightarrow 3}}\,\sqrt{5x-4}\)

\(\sqrt {11}\)

  1. \({\lim\limits_{t\rightarrow 2}}\,\sqrt{3t+4}\)

  1. \({\lim\limits_{t\rightarrow 2}} \, [ t\sqrt{( 5t+3) ( t+4 ) }] \)

\(2\sqrt {78} \)

  1. \({\lim\limits_{t\rightarrow -1}}\, [ t\sqrt[3]{( {t+1}) ( 2t-1) }] \)

  1. \({\lim\limits_{x\rightarrow 3}}\, (\sqrt{x}+x+4) ^{1/2}\) \(\ \ \ \ \ \ \qquad \)

\( (\sqrt 3 + 7) ^{1/2} \)

  1. \({\lim\limits_{t\rightarrow 2}}\, (t\sqrt{2t}+4) ^{1/3}\)

  1. \({\lim\limits_{t\rightarrow -1}}[4t ( t+1) ] ^{2/3}\)

0

  1. \(\lim\limits_{x\rightarrow 0}\, ( x^{2}-2x) ^{3/5}\)

  1. \({\lim\limits_{t\rightarrow 1}} \,( {3t^{2}-2t+4})\)

5

  1. \({\lim\limits_{x\rightarrow 0}}\,( {-3x^{4}+2x+1}) \)

  1. \({\lim\limits_{x\rightarrow \frac{1}{2}}} ( {2x^{4}-8x^{3}+4x-5} ) \)

\(- \dfrac{31}{8}\)

  1. \({\lim\limits_{x\rightarrow -\frac{1}{3}}} ( {27x^{3}+9x+1}) \)

  1. \({\lim\limits_{x\rightarrow 4}}\,{\dfrac{{x^{2}+4}}{\sqrt{{x}}}}\)

10

  1. \({\lim\limits_{x\rightarrow 3}}\,{\dfrac{{x^{2}+5}}{\sqrt{{3x}}}}\)

  1. \({\lim\limits_{x\rightarrow -2}}{\dfrac{{2x^{3}+5x}}{{3x-2}}}\)

\(\dfrac{13}{4}\)

  1. \({\lim\limits_{x\rightarrow 1}}\, {\dfrac{{2x^{4}-1}}{{3x^{3}+2}}}\)

  1. \({\lim\limits_{x\rightarrow 2}}\,{\dfrac{{x^{2}-4}}{{x-2}}}\)

4

  1. \({\lim\limits_{x\rightarrow -2}}\,{\dfrac{{x+2}}{{x^{2}-4}}}\)

  1. \({\lim\limits_{x\rightarrow -1}}{\dfrac{{x^{3}-x}}{{x+1}}}\)

2

  1. \({\lim\limits_{x\rightarrow -1}}\,{\dfrac{{x^{3}+x^{2}}}{{x^{2}-1}} }\)

  1. \({\lim\limits_{x\rightarrow -8}}\left( {{\dfrac{{2x}}{{x+8}}}+{\dfrac{{16}}{{x+8}}}}\right)\)

2

  1. \({ \lim\limits_{x\rightarrow 2}}\left( {{\dfrac{{3x}}{{x-2}}}-{\dfrac{{6}}{{x-2}}}}\right) \)

  1. \({\lim\limits_{x\rightarrow 2}}\,{\dfrac{{\sqrt{x}-\sqrt{2}}}{{x-2}}\qquad }\)

\(\dfrac{1}{2\sqrt 2 } \)

  1. \({\lim\limits_{x\rightarrow 3}}\,\dfrac{\sqrt{x}-\sqrt{3}}{x-3}\)

  1. \({\lim\limits_{x\rightarrow 4}}\,{\dfrac{\sqrt{x+5}-3}{ ( {x-4} ) ( x+1) }}\)

\(\dfrac{1}{30}\)

  1. \({\lim\limits_{x\rightarrow 3}}\,{\dfrac{{\sqrt{x+1}-2}}{x(x-3) }}\)

In Problems 45-50, find each one-sided limit using properties of limits.

  1. \({\lim\limits_{x\rightarrow 3^{-}}} ( {x^{2}-4} ) \)

5

  1. \({\lim\limits_{x\rightarrow 2^{+}}} ( {3x^{2}+x}) \)

  1. \({\lim\limits_{x\rightarrow 3^{-}}}{\dfrac{{x^{2}-9}}{{x-3}}}\)

6

  1. \({\lim\limits_{x\rightarrow 3^{+}}}{\dfrac{{x^{2}-9}}{{x-3}}}\)

  1. \({\lim\limits_{x\rightarrow 3^{-}}}( {\sqrt{9-x^{2}}+x}) ^{2}\)

9

  1. \({\lim\limits_{x\rightarrow 2^{+}}}( {2\sqrt{x^{2}-4}+3x}) \)

91

In Problems 51-58, use the information below to find each limit. \[ \lim\limits_{x\rightarrow c}f(x) =5\qquad \lim\limits_{x\rightarrow c}g(x)=2 \qquad \lim\limits_{x\rightarrow c}h( x) =0 \]

  1. \({\lim\limits_{x\rightarrow c}}\, [ {{f(x) -3g}}( x) ] \)

\(-1\)

  1. \({\lim\limits_{x\rightarrow c}}\, [ {5{f(x) }} ] \)

  1. \({\lim\limits_{x\rightarrow c}}\,{[ {g ( {x}) }] }^{3}\)

8

  1. \({\lim\limits_{x\rightarrow c}}\,\dfrac{{f(x) }}{{g(x) -h ( {x}) }} \)

  1. \({\lim\limits_{x\rightarrow c}}\,\dfrac{h( x) }{g( x) }\)

0

  1. \({\lim\limits_{x\rightarrow c}}\,[ 4f( x) \cdot g( x) ] \)

  1. \({\lim\limits_{x\rightarrow c}}\left[\dfrac{1}{g( x) }\right] ^{2}\)

\(\dfrac{1}{4}\)

  1. \({\lim\limits_{x\rightarrow c}}\,\sqrt[3]{5g( x) -3}\)

In Problems 59 and 60, use the graph of the functions and properties of limits to find each limit, if it exists. If the limit does not exist, say, “the limit does not exist,” and explain why.

    1. (a) \(\lim\limits_{x\rightarrow 4}\left[ f( x) +g( x) \right] \)
    2. (b) \(\lim\limits_{x\rightarrow 4}\left\{ f( x) \left[g( x) -h( x) \right] \right\} \)
    3. (c) \(\lim\limits_{x\rightarrow 4}[f( x) \cdot g( x)] \)
    4. (d) \(\lim\limits_{x\rightarrow 4}[2h( x) ] \)
    5. (e) \(\lim\limits_{x\rightarrow 4}\dfrac{g( x) }{f( x) }\)
    6. (f) \(\lim\limits_{x\rightarrow 4}\dfrac{h( x) }{f( x) }\)

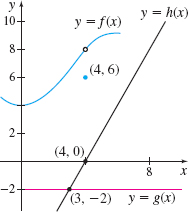
  1. (a) 6
  2. (b) \(-16\)
  3. (c) \(-16\)
  4. (d) 0
  5. (e) \(-\dfrac{1}{4}\).
  6. (f) 0
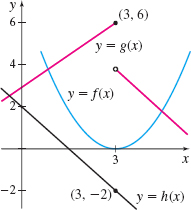
    1. (a) \(\lim\limits_{x\rightarrow 3}\left\{ 2\left[ f( x) +h( x) \right] \right\} \)
    2. (b) \(\lim\limits_{x\rightarrow {3^-}}[ g( x) +h( x) ] \)
    3. (c) \(\lim\limits_{x\rightarrow 3}\sqrt[3]{h(x)}\)
    4. (d) \(\lim\limits_{x\rightarrow 3}\dfrac{f( x) }{h( x) }\)
    5. (e) \(\lim\limits_{x\rightarrow 3}[ h( x) ] ^{3}\)
    6. (f) \(\lim\limits_{x\rightarrow 3}[ f( x) -2h( x) ] ^{3/2}\)

In Problems 61-66, for each function \(f\), find the limit as \(x\) approaches \(c\) of the average rate of change of \(f\) from \(c\) to \(x\). That is, find \[ \lim\limits_{x\rightarrow c}\dfrac{f( x) -f( c) }{x-c} \]

  1. \(f( x) =3x^{2},\) \(c=1\)

6

  1. \(f( x) =8x^{3},\) \(c=2\)

  1. \(f( x) =-2x^{2}+4\), \(c=1\)

\(-4\)

  1. \(f( x) =20-0.8x^{2}\), \(c=3\)

  1. \(f( x) =\sqrt{x},\) \(c=1\)

\(\dfrac{1}{2}\)

  1. \(f( x) =\sqrt{2x},\) \(c=5\)

In Problems 67-72, find the limit of the difference quotient for each function \(f\). That is, find \(\lim\limits_{h\rightarrow 0} \dfrac{{f( {x+h}) -f(x) }}{{h}}\).

  1. \(f(x)\) \(=4x-3 \)

4

  1. \(f(x)=3x+5 \)

  1. \(f(x)=3x^{2}+4x+1\)

\(6x + 4\)

  1. \(f(x)=2x^{2}+x\)

  1. \(f(x) =\dfrac{2}{x}\)

\( - \dfrac{2}{x^2}\)

  1. \(f(x) =\dfrac{3}{x^{2}}\)

In Problems 73-80, find \(\lim\limits_{x\rightarrow c^{-}}f(x)\) and \(\lim\limits_{x\rightarrow c^{+}}f(x)\) for the given number \(c\). Based on the results, determine whether \(\lim\limits_{x\rightarrow c}f(x)\) exists.

  1. \(f(x) ={\left\{ \begin{array}{c@{ }rl} 2x-3 & \hbox{if} & x\leq 1 \\[3pt] 3-x & \hbox{if} & x>1 \end{array} \right. }\) at \(c=1\)

\(\lim \limits_{x \to 1^ - } f(x) =- 1\), \(\lim \limits_{x \to 1^ + } f(x) = 2\), \(\mathop {\lim\limits_{x \to 1}} f(x)\) does not exist

  1. \(f(x) ={\left\{ \begin{array}{c@{ }rl} 5x+2 & \hbox{if} & x\lt 2 \\[3pt] 1+3x & \hbox{if} & x\geq 2 \end{array} \right. }\) at \(c=2\)

  1. \(f(x) ={\left\{ \begin{array}{c@{ }rl} 3x-1 & \hbox{if} & x\lt 1 \\[3pt] 4 & \hbox{if} & x=1 \\[3pt] 2x & \hbox{if} & x>1 \end{array} \right. }\) at \(c=1\)

\(\mathop {\lim\limits_{x \to 1^ - }} f(x) = 2\), \(\mathop {\lim\limits_{x \to 1^ + }} f(x) = 2\), \(\mathop {\lim\limits_{x \to 1}} f(x) = 2\)

  1. \(f(x) ={\left\{ \begin{array}{c@{ }rl} 3x-1 & \hbox{if} & x\lt 1 \\[3pt] 2 & \hbox{if} & x=1 \\[3pt] 2x & \hbox{if} & x>1 \end{array} \right. }\) at \(c=1\)

  1. \(f(x) ={\left\{ \begin{array}{c@{ }rl} x-1 & \hbox{if} & x\lt 1 \\[3pt] \sqrt{\,x-1} & \hbox{if} & x>1 \end{array} \right. }\) at \(c=1\)

\(\mathop {\lim\limits_{x \to 1^ - }} f(x) = 0\), \(\mathop {\lim\limits_{x \to 1^ + }} f(x) = 0\), \(\mathop {\lim\limits_{x \to 1}} f(x) = 0\)

  1. \(f(x) ={\left\{ \begin{array}{c@{ }rl} \sqrt{9-x^{2}} & \hbox{if} & 0 \lt x\lt 3 \\[3pt] \sqrt{x^{2}-9} & \hbox{if} & x>3 \end{array} \right. }\) at \(c=3\)

  1. \(f(x) ={\left\{ \begin{array}{c@{ }rl} \dfrac{x^{2}-9}{x-3} & \hbox{if} & x\neq 3 \\ 6 & \hbox{if} & x=3 \end{array} \right. }\) at \(c=3\)

\(\mathop {\lim\limits_{x \to 3^ - }} f(x) = 6\) \(\mathop {\lim\limits_{x \to 3^ + }} f(x) = 6\), \(\mathop {\lim\limits_{x \to 3}} f(x) = 6\)

  1. \(f(x) = {\left\{ \begin{array}{c@{ }rl} \dfrac{x-2}{x^{2}-4} & \hbox{if} & x\neq 2 \\ 1 & \hbox{if} & x=2 \end{array} \right. }\) at \(c=2\)

Applications and Extensions

Heaviside Functions In Problems 81 and 82, find the limit of the given Heaviside function at \(c\).

  1. \(u_{1}( t) =\left\{ \begin{array}{ll@{ }l} 0 & & \hbox{if }t\lt 1 \\ 1 & & \hbox{if }t\geq 1 \end{array} \right. \) at \(c=1\)

The limit does not exist.

  1. \(u_{3}( t) =\left\{ \begin{array}{ll@{ }l} 0 & & \hbox{if }t\lt 3 \\[3pt] 1 & & \hbox{if }t\geq 3 \end{array} \hbox{at }c=3\right. \)

In Problems 83-92, find each limit.

  1. \({\lim\limits_{h\rightarrow 0}}\,{\dfrac{{( {x+h}) ^{2}-x^{2}}}{{h}}}\)

2\(x\)

  1. \({\lim\limits_{h\rightarrow 0}}\,{\dfrac{{\sqrt{x+h}-\sqrt{x}}}{{h}}}\)

  1. \({\lim\limits_{h\rightarrow 0}}\,\dfrac{{{{ \dfrac{{1}}{{x+h}}}}-{{\dfrac{{1}}{{x}}}}}}{h}\)

\(-\dfrac{1}{x^2}\)

  1. \({\lim\limits_{h\rightarrow 0}}\,{\dfrac{{{ \dfrac{{1}}{{( {x+h}) ^{3}}}}-{\dfrac{{1}}{{x^{3}}}}}}{{h}}}\)

  1. \({\lim\limits_{x\rightarrow 0}}\left[ {\dfrac{{1}}{{x}}}\left( \dfrac{{1}}{{4+x}}-\dfrac{1}{4}\right)\! \right]\)

\( - \dfrac{1}{16}\)

  1. \(\lim\limits_{x\rightarrow -1}\left[ \dfrac{2}{x+1}\left( \dfrac{1}{3}-\dfrac{1}{x+4}\right) \!\right] \)

  1. \({\lim\limits_{x\rightarrow 7}}\,{\dfrac{{x-7}}{{\sqrt{x+2}-3}}}\)

6

  1. \({\lim\limits_{x\rightarrow 2}}\,\dfrac{x-2}{\sqrt{x+2}-2}\)

  1. \({\lim\limits_{x\rightarrow 1}}\,\dfrac{x^{3}-3x^{2}+3x-1}{x^{2}-2x+1}\)

0

  1. \({\lim\limits_{x\rightarrow -3}}\dfrac{x^{3}+7x^{2}+15x+9}{ x^{2}+6x+9}\)

92

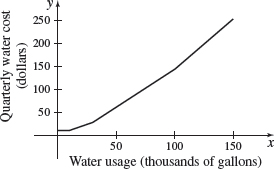
  1. Cost of Water The Jericho Water District determines quarterly water costs, in dollars, using the following rate schedule:

    Water used (in thousands of gallons) Cost
    \(0\leq x\leq 10\) \(\$9.00\)
    \(10 \lt x\leq 30\) $9.00+0.95 for each thousand gallons in excess of 10,000 gallons
    \(30 \lt x\leq 100\) $28.00+1.65 for each thousand gallons in excess of 30,000 gallons
    \(x>100\) \(\$143.50+2.20\) for each thousand gallons in excess of 100,000 gallons

    Source: Jericho Water District, Syosset, NY.

    1. (a) Find a function \(C\) that models the quarterly cost, in dollars, of using \(x\) thousand gallons of water.
    2. (b) What is the domain of the function \(C?\)
    3. (c) Find each of the following limits. If the limit does not exist, explain why. \begin{equation*} \begin{array}{ll@{\quad}ll@{\quad}ll@{\quad}l} \lim\limits_{x\rightarrow 5}C( x) & & \lim\limits_{x\rightarrow 10}C( x) & & \lim\limits_{x\rightarrow 30}C( x) & & \lim\limits_{x\rightarrow 100}C( x) \end{array} \end{equation*}
    4. (d) What is \(\lim\limits_{x\rightarrow 0^{+}}C( x) ?\)
    5. (e) Graph the function \(C\).

  1. (a) \(C(x)={\left\{ \begin{array}{ll} 9.00 & \hbox{if} & 0 \leq x \leq 10 \\ 9.00 + 0.95(x-10) & \hbox{if} & 10 \lt x \leq30 \\ 28.00 + 1.65(x-30) & \hbox{if} & 30 \lt x \leq 100 \\ 143.50 + 2.20(x-100) & \hbox{if} & x \gt 100 \end{array} \right. }\)
  2. (b) \(\{x \vert x \ge 0\}\)
  3. (c) \(\mathop {\lim\limits_{x \to 5}} C(x) = 9.00\), \(\mathop {\lim\limits_{x \to 10}} C(x) = 9.00\), \(\mathop {\lim\limits_{x \to 30}} C(x) = 28.00\), \(\mathop {\lim\limits_{x \to 100}} C(x) = 143.50\)
  4. (d) 9.00
  5. (e)

  1. Cost of Natural Gas In February 2012 Peoples Energy had the following monthly rate schedule for natural gas usage in single- and two-family residences with a single gas meter:

    Monthly customer charge \(\$22.13\)
    Per therm distribution charge
      \(\leq \) \(50\) therms \(\$0.25963\) per therm
      \(>50\) therms \(\$12.98+0.11806\) for each therm in excess of \(50\)
    Gas charge: \(\$0.3631\) per therm

    Source: Peoples Energy, Chicago, IL.

    1. (a) Find a function \(C\) that models the monthly cost, in dollars, of using \(x\) therms of natural gas.
    2. (b) What is the domain of the function \(C?\)
    3. (c) Find \(\lim\limits_{x\rightarrow 50}C( x) \), if it exists. If the limit does not exist, explain why.
    4. (d) What is \(\lim\limits_{x\rightarrow 0^{+}}C( x) ?\)
    5. (e) Graph the function \(C.\)

  1. Low-Temperature Physics In thermodynamics, the average molecular kinetic energy (energy of motion) of a gas having molecules of mass \(m\) is directly proportional to its temperature \(T\) on the absolute (or Kelvin) scale. This can be expressed as \(\dfrac{1}{2}mv^{2}=\dfrac{3}{2}kT,\) where \(v=v(T)\) is the speed of a typical molecule at time \(t\) and \(k\) is a constant, known as the Boltzmann constant.

    1. (a) What limit does the molecular speed \(v\) approach as the gas temperature \(T\) approaches absolute zero (\(0{K}\) or \(-273^{\circ}{\rm C}\) or \(-469^{\circ}{\rm F}\))?
    2. (b) What does this limit suggest about the behavior of a gas as its temperature approaches absolute zero?

  1. (a) 0
  2. (b) Answers will vary.

  1. For the function \(f(x) =\left\{ \begin{array}{c@{\qquad}rl} 3x+5 & \hbox{if} & x\leq 2 \\[3pt] 13-x & \hbox{if} & x>2 \end{array} \right. \), find

    1. (a) \({\lim\limits_{h\rightarrow 0^{-}}}{\dfrac{{f({2+h}) -f( {2}) }}{{h}}}\)
    2. (b) \({\lim\limits_{h\rightarrow 0^{+}}}\) \(\dfrac{{f( {2+h}) -f( {2}) }}{{h}}\)
    3. (c) Does \({\lim\limits_{h \rightarrow 0}}{\dfrac{{f( {2+h}) -f( {2}) }}{{h}}}\) exist?

  1. Use the fact that \(\vert x\vert =\left\{\! \begin{array}{l@{\quad}l} x & \hbox{if }x\geq 0 \\ -x & \hbox{if }x\lt 0 \end{array} \right. \) to show that \(\lim\limits_{x\rightarrow 0}\vert x\vert =0.\)

See Student Solutions Manual.

  1. Use the fact that \(\vert x\vert =\sqrt{x^{2}}\) to show that \(\lim\limits_{x\rightarrow 0}\vert x\vert =0.\)

  1. Find functions \(f\) and \(g\) for which \(\lim\limits_{x\rightarrow c}\) \([ f(x)+g(x)] \) may exist even though \(\lim\limits_{x\rightarrow c}f(x)\) and \(\lim\limits_{x\rightarrow c}g(x)\) do not exist.

Answers will vary.

  1. Find functions \(f\) and \(g\) for which \(\lim\limits_{x\rightarrow c}\) \([ f(x)g(x)] \) may exist even though \(\lim\limits_{x\rightarrow c}f(x)\) and \(\lim\limits_{x\rightarrow c}\,g( x) \) do not exist.

  1. Find functions \(f\) and \(g\) for which \(\lim\limits_{x\rightarrow c}\) \(\left[ \dfrac{f(x)}{g( x) }\right] \) may exist even though \(\lim\limits_{x\rightarrow c}f(x)\) and \(\lim\limits_{x \rightarrow c}g( x) \) do not exist.

Answers will vary.

  1. Find a function \(f\) for which \(\lim\limits_{x\rightarrow c}\vert f(x)\vert \) may exist even though \(\lim\limits_{x\rightarrow c}f(x)\) does not exist.

  1. Prove that if \(g\) is a function for which \(\lim\limits_{x\rightarrow c}g(x)\) exists and if \(k\) is any real number, then \(\lim\limits_{x\rightarrow c}[kg(x)]\) exists and \(\lim\limits_{x \rightarrow c}[kg(x)]=k\lim\limits_{x\rightarrow c}g(x)\).

See Student Solution Manual.

  1. Prove that if the number \(c\) is in the domain of a rational function \(R( x) =\) \(\dfrac{p(x)}{q(x)}\), then \(\lim\limits_{x\rightarrow c}R( x) =R( c) \).

Challenge Problems

  1. Find \({\lim\limits_{x\rightarrow a}}{\dfrac{{x^{n}-a^{n}}}{{x-a}}}\), \(n\) a positive integer.

\(na\)\(^{n - 1}\)

  1. Find \({\lim\limits_{x\rightarrow -a}}{\dfrac{{x^{n}+a^{n}}}{{x+a}}}\), \(n\) a positive integer.

  1. Find \({\lim\limits_{x\rightarrow 1}}\dfrac{x^{m}-1}{x^{n}-1}\), \(m\), \(n\) positive integers.

\(\dfrac{m}{n}\)

  1. Find \({\lim\limits_{x\rightarrow 0}}{\dfrac{{\sqrt[3]{{1+x}}-1}}{{x}}}\).

  1. Find \({\lim\limits_{x\rightarrow 0}}{\dfrac{{\sqrt{( {1+ax}) ( {1+bx}) }-1}}{{x}}}\).

\(\dfrac{a + b}{2}\)

  1. Find \({\lim\limits_{x\rightarrow 0}}{\dfrac{{\sqrt{ ( {1+a_{1}x}) ( {1+a_{2}x}) \cdots ( {1+a_{n}x}) }-1}}{{x}}}\).

  1. Find \({\lim\limits_{h\rightarrow 0}}{\dfrac{{f ({h}) -f (0)}}{{h}}}\) if \(f(x)=x|x|\).

0.