Question

\(\lim\limits_{x\rightarrow 0}\) sin \(x =\) __________

Question

True or False \(\lim\limits_{x\rightarrow 0}\dfrac{\cos x-1}{x} = 1\).

Question

The Squeeze Theorem states that if the functions \(f,g\), and \(h\) have the property \(f(x)\leq g(x)\leq h(x)\) for all \(x\) in an open interval containing \(c\), except possibly at \(c\), and if \(\lim\limits_{x\rightarrow c}f(x) = \) \(\lim\limits_{x\rightarrow c}h(x) = L\), then \(\lim\limits_{x\rightarrow c}g(x) =\) _________.

Question

True or False \(f(x) = \csc x\) is continuous for all real numbers except \(x = 0\).

Question

Suppose \(-x^{2}+1\leq g(x) \leq x^{2}+1\) for all \(x\) in an open interval containing \(0\). Find \(\lim\limits_{x\rightarrow 0}g(x)\).

Question

Suppose \(-(x-2) ^{2}-3\leq g(x)\leq (x-2) ^{2}-3\) for all \(x\) in an open interval containing \(2\). Find \(\lim\limits_{x\rightarrow 2}g(x)\).

Question

Suppose \(\cos x\leq g(x) \leq 1\) for all \(x\) in an open interval containing \(0\). Find \(\lim\limits_{x\rightarrow 0}g(x)\).

Question

Suppose \(-x^{2}+1\leq g(x) \leq \sec x\) for all \(x\) in an open interval containing \(0\). Find \(\lim\limits_{x\rightarrow 0}g(x)\).

Question

\({\lim\limits_{x\rightarrow 0}}({x^{3}+\sin x})\)

Question

\({\lim\limits_{x\rightarrow 0}}({x^{2}-\cos x})\)

Question

\({\lim\limits_{x\rightarrow \pi /3}}({\cos x+\sin x})\)

Question

\({\lim\limits_{x\rightarrow \pi /3}}({\sin x-\cos x})\)

Question

\({\lim\limits_{x\rightarrow 0}}\ \dfrac{\cos x}{1+\sin x}\)

Question

\({\lim\limits_{x\rightarrow 0}}\ \dfrac{\sin x}{1+\cos x}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{3}{1+e^{x}}\)

Question

\(\lim\limits_{x \rightarrow 0}\dfrac{e^{x}-1}{1+e^{x}}\)

Question

\(\lim\limits_{x\rightarrow 0}(e^{x}\sin x)\)

Question

\(\lim\limits_{x\rightarrow 0}(e^{-x}\tan x)\)

Question

\(\lim\limits_{x\rightarrow 1}\ln \left(\dfrac{e^{x}}{x}\right)\)

Question

\(\lim\limits_{x\rightarrow 1}\ln \left(\dfrac{x}{e^{x}}\right)\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{e^{2x}}{1+e^{x}}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{1-e^{x}}{1-e^{2x}}\)

Question

\({\lim\limits_{x\rightarrow 0}}\dfrac{\sin (7x)}{x}\)

Question

\({\lim\limits_{x\rightarrow 0}} \dfrac{\sin \dfrac{{x}}{3}}{x}\)

Question

\(\lim\limits_{\theta \rightarrow 0}\dfrac{\theta +3\sin \theta}{2\theta}\)

Question

\({\lim\limits_{x\rightarrow 0}}\ \dfrac{2x-5\sin (3x)}{x}\)

Question

\({\lim\limits_{\theta \rightarrow 0}}\ \dfrac{\sin \theta}{\theta +\tan \theta}\)

Question

\(\lim\limits_{\theta \rightarrow 0}\dfrac{\tan \theta}{\theta}\)

Question

\(\lim\limits_{\theta \rightarrow 0}\dfrac{5}{\theta \cdot \csc \theta}\)

Question

\(\lim\limits_{\theta \rightarrow 0}\dfrac{\sin (3\theta)}{\sin (2\theta)}\)

Question

\(\lim\limits_{\theta \rightarrow 0}\dfrac{1-\cos ^{2}\theta}{\theta}\)

Question

\(\lim\limits_{\theta \rightarrow 0}\dfrac{ \cos (4\theta)-1}{2\theta}\)

Question

\(\lim\limits_{\theta \rightarrow 0}(\theta \cdot \cot \theta)\)

Question

\(\lim\limits_{\theta \rightarrow 0}\left[\sin \theta \left(\dfrac{\cot \theta -\csc \theta}{\theta}\right) \right] \)

Question

\(f(x)=\left\{ \begin{array}{c@{\quad}l} 3\cos x & \hbox{ if } x\lt 0 \\[4pt] 3 & \hbox{ if }x=0 \\[4pt] x+3 & \hbox{ if }x>0 \end{array} \right. \quad at\quad c=0 \)

Question

\(f(x)=\left\{ \begin{array}{c@{\quad}l} \cos x & \hbox{ if }x\lt 0 \\[4pt] 0 & \hbox{ if }x=0 \\[4pt] e^{x} & \hbox{ if }x\gt 0 \end{array} \right. \quad at\quad c=0\)

Question

\(f(\theta )=\left\{ \begin{array}{l@{\quad}l} \sin \theta & \hbox{ if }\theta \leq\dfrac{\pi }{4} \\[8pt] \cos \theta & \hbox{ if }\theta >\dfrac{\pi }{4} \end{array} \right. at\quad c=\dfrac{\pi }{4}\)

Question

\(f(x)=\left\{ \begin{array}{c@{\quad}l} \tan ^{-1}x & \hbox{ if }x\lt 1 \\[4pt] \ln x & \hbox{ if }x\geq 1 \end{array} \right. at\quad c=1\)

Question

\(f(x) = \sin \left(\dfrac{x^{2}-4x}{x-4}\right)\)

Question

\(f(x) = \cos \left(\dfrac{x^{2}-5x+1}{2x}\right)\)

Question

\(f(\theta) = \dfrac{1}{1+\sin \theta}\)

Question

\(f(\theta) = \dfrac{1}{1+\cos^{2}\theta}\)

Question

\(f(x) = \dfrac{\ln x}{x-3}\)

Question

\(f(x) = \ln (x^{2}+1)\)

Question

\(f(x) = e^{-x}\sin x\)

Question

\(f(x) = \dfrac{e^{x}}{1+\sin ^{2}x}\)

Question

\(\lim\limits_{x\rightarrow 0}\left(x^{2}\sin \dfrac{1}{x}\right)\)

Question

\(\lim\limits_{x\rightarrow 0}\left[ x\left(1-\cos \dfrac{1}{x}\right) \right]\)

Question

\(\lim\limits_{x\rightarrow 0}\left[ x^{2}\left(1-\cos \dfrac{1}{x}\right) \right]\)

Question

\(\lim\limits_{x\rightarrow 0}\left[ \sqrt{x^{3}+3x^{2}}\sin \left(\dfrac{1}{x}\right) \right]\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\sin (ax)}{\sin (bx)} = \dfrac{a}{b}\);  \(b\neq0\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\cos (ax)}{\cos (bx)} = 1\qquad\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\sin (ax)}{bx} = \dfrac{a}{b}\);  \(b\neq 0\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{1-\cos (ax)}{bx} = 0\) \(a\neq 0\), \(b\neq 0\)

Question

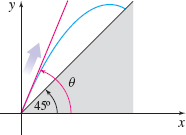
Projectile Motion An object is propelled from ground level at an angle \(\theta \), \(\dfrac{\pi}{4}\lt \theta \lt \dfrac{\pi}{2}\), up a ramp that is inclined to the horizontal at an angle of \(45^{\circ}\). See the figure. If the object has an initial velocity of 10 feet/second, the equations of the horizontal position \(x = x(\theta)\) and the vertical position \(y = y(\theta)\) of the object after \(t\) seconds are given by \begin{equation*} x = x(\theta) = (10\cos \theta) t \quad \hbox{and} \quad y = y(\theta) = -16t^{2}+ (10\sin \theta) t \end{equation*}

For \(t\) fixed,

1. Find \(\lim\limits_{\theta \rightarrow {\pi}/{4}^{+}}x(\theta)\) and \(\lim\limits_{\theta \rightarrow {\pi}/{4} ^{+}}y (\theta)\).
2. Are the limits found in (a) consistent with what is expected physically?
3. Find \(\lim\limits_{\theta \rightarrow {\pi}/{2}^{-}}x(\theta)\) and \(\lim\limits_{\theta \rightarrow {\pi}/{2}^{-}}y(\theta)\).
4. Are the limits found in (c) consistent with what is expected physically?

Question

Show that \(\lim\limits_{x\rightarrow 0}\dfrac{1-\cos x}{ x^{2}} = \dfrac{1}{2}\).

Question

Squeeze Theorem If \(0\leq f(x)\leq 1\) for every number \(x\), show that \(\lim\limits_{x\rightarrow 0}[ x^{2}f(x)] = 0\).

Question

Squeeze Theorem If \(0\leq f(x)\leq M\) for every \(x\), show that \(\lim\limits_{x\rightarrow 0}[ x^{2}f(x)] = 0\).

Question

The function \(f(x) = \dfrac{\sin (\pi x)}{x}\) is not defined at \(0\). Decide how to define \(f(0)\) so that \(f\) is continuous at \(0\).

Question

Define \(f(0)\) and \(f(1)\) so that the function \(f(x) = \dfrac{\sin (\pi x)}{x(1-x)}\) is continuous on the interval $[0,1]\).

Question

Is \(f(x)=\left\{ \begin{array}{c@{\quad}l} \dfrac{\sin x}{x} & \hbox{if }x\neq 0 \\[10pt] 1 & \hbox{if }x=0 \end{array} \right.\) continuous at 0?

Question

Is \(f(x) = {\left\{ \begin{array}{c@{\quad}l} \dfrac{1-\cos x}{x} & \hbox{if }x\neq 0 \\[10pt] 0 & \hbox{if }x = 0 \end{array} \right.}\) continuous at \(0\)?

Question

Squeeze Theorem Show that \(\lim\limits_{x\rightarrow0}\left[x^{n}\sin \left(\dfrac{1}{x}\right) \right] = 0\), where \(n\) is a positive integer. (Hint: Look first at Problem 57.)

Question

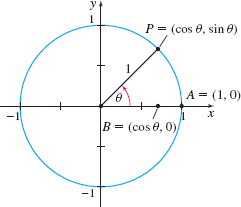
Prove \(\lim\limits_{\theta \rightarrow 0}\sin \theta = 0.\) (Hint: Use a unit circle as shown in the figure, first assuming \(0\lt \theta \,\lt \dfrac{\pi}{2}\). Then use the fact that \(\sin \theta\) is less than the length of the arc \(AP\), and the Squeeze Theorem, to show that \(\lim\limits_{\theta \rightarrow 0^{+}}\sin \theta = 0\). Then use a similar argument with \(-\dfrac{\pi}{2}\lt \theta \lt 0\) to show \(\lim\limits_{\theta \rightarrow 0^{-}}\sin \theta = 0.)\)

Question

Prove \(\lim\limits_{\theta \rightarrow 0}\cos \theta = 1\). Use either the proof outlined in Problem 64 or a proof using the result \(\lim\limits_{\theta \rightarrow 0}\sin \theta = 0\) and a Pythagorean identity.

Question

Without using limits, explain how you can decide whether \(f(x) = \cos (5x^{3}+2x^{2}-8x+1)\) is continuous.

Question

Explain the Squeeze Theorem. Draw a graph to illustrate your explanation.

Question

Use the Sum Formulas \(\sin (a+b) = \sin a\cos b+\cos a\sin b\) and \(\cos (a+b) = \cos a\cos b-\sin a\sin b\) to show that the sine function and cosine function are continuous on their domains.

Question

Find \(\lim\limits_{x\rightarrow 0}\dfrac{\sin x^{2}}{x}\).

Question

Squeeze Theorem If \(f(x)=\left\{ \begin{array}{l@{\quad}l} 1 & \hbox{if }x\hbox{ is rational} \\[3pt] 0 & \hbox{if }x\hbox{ is irrational} \end{array} \right.\) show that \(\lim\limits_{x\rightarrow 0}[ xf(x)] =0\).

Question

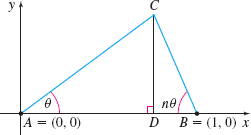
Suppose points \(A\) and \(B\) with coordinates \((0,0)\) and \((1,0)\), respectively, are given. Let \(n\) be a number greater than \(0\), and let \(\theta \) be an angle with the property \(0\lt \theta \lt \dfrac{\pi}{1+n}\). Construct a triangle \(ABC\) where \(\overline{AC}\) and \(\overline{AB}\) form the angle \(\theta \), and \(\overline{CB}\) and \(\overline{AB}\) form the angle \(n\,\theta \) (see the figure below). Let \(D\) be the point of intersection of \(\overline{AB}\) with the perpendicular from \(C\) to \(\overline{AB}\). What is the limiting position of \(D\) as \(\theta \) approaches \(0\)?