Calculus—What Is It?

Calculus is a part of mathematics that evolved much later than other subjects. Algebra, geometry, and trigonometry were developed in ancient times, but calculus as we know it did not appear until the seventeenth century.

The first evidence of calculus has its roots in ancient mathematics. For example, in his book, A History of π, Petr Beckmann explains that Greek mathematician Archimedes (287–212 BCE) “took the step from the concept of ‘equal to’ to the concept of ‘arbitrarily close to’ or ‘as closely as desired’…and thus reached the threshold of the differential calculus, just as his method of squaring the parabola reached the threshold of the integral calculus.”* But it was not until Sir Isaac Newton and Gottfried Wilhelm Leibniz, each working independently, expanded, organized, and applied these early ideas, that the subject we now know as calculus was born.

Although we attribute the birth of calculus to Newton and Leibniz, many other mathematicians, particularly those in the eighteenth and nineteenth centuries, contributed greatly to the body and rigor of calculus. You will encounter many of their names and contributions as you pursue your study of calculus.

But, what is calculus? Why is it given such notoriety?

The simple answer is: calculus models change. Since the world and most things in it are constantly changing, mathematics that explains change becomes immensely useful.

Calculus has two major branches, differential calculus and integral calculus. Let’s take a peek at what calculus is by looking at two problems that prompted the development of calculus.

The Tangent Problem — The Basis of Differential Calculus

Suppose we want to find the slope of the line tangent to the graph of a function at some point P = (x₁, y₁). See Figure 1(a). Since the tangent line necessarily contains the point P, it remains only to find the slope to identify the tangent line. Suppose we repeatedly zoom in on the graph of the function at the point P. See Figure 1(b). If we can zoom in close enough, then the graph of the function will look approximately linear, and we can choose a point Q, on the graph of the function different from the point P, and use the formula for slope.

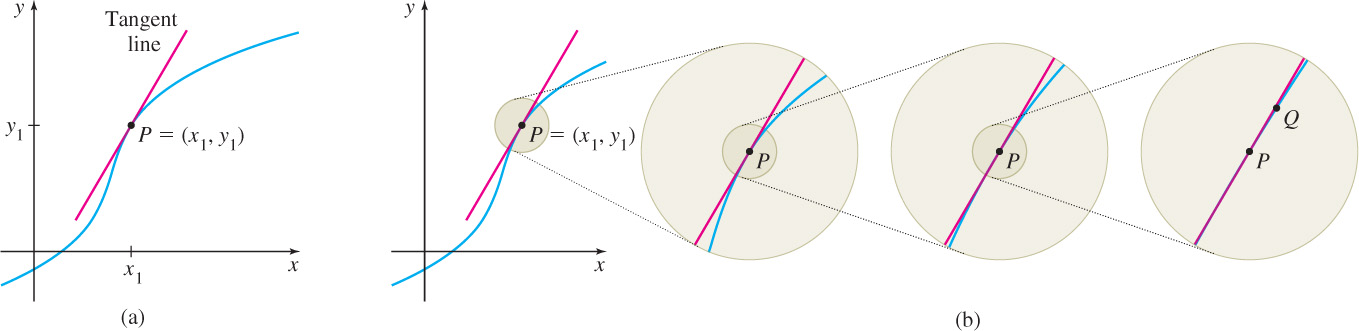
Repeatedly zooming in on the point P is equivalent to choosing a point Q closer and closer to the point P. Notice that as we zoom in on P, the line connecting the points P and Q, called a secant line, begins to look more and more like the tangent line to the graph of the function at the point P. If the point Q can be made as close as we please to the point P, without equaling the point P, then the slope of the tangent line m_tan can be found. This formulation leads to differential calculus, the study of the derivative of a function.

The derivative gives us information about how a function changes at a given instant and can be used to solve problems involving velocity and acceleration; marginal cost and profit; and the rate of change of a chemical reaction. Derivatives are the subjects of Chapters 2 through 4.

The Area Problem—The Basis of Integral Calculus

If we want to find the area of a rectangle or the area of a circle, formulas are available. (see Figure 2). But what if the figure is curvy, but not circular as in Figure 3? How do we find this area?

Calculus provides a way. Look at Figure 4(a). It shows the graph of y = x² from x = 0 to x = 1. Suppose we want to find the shaded area.

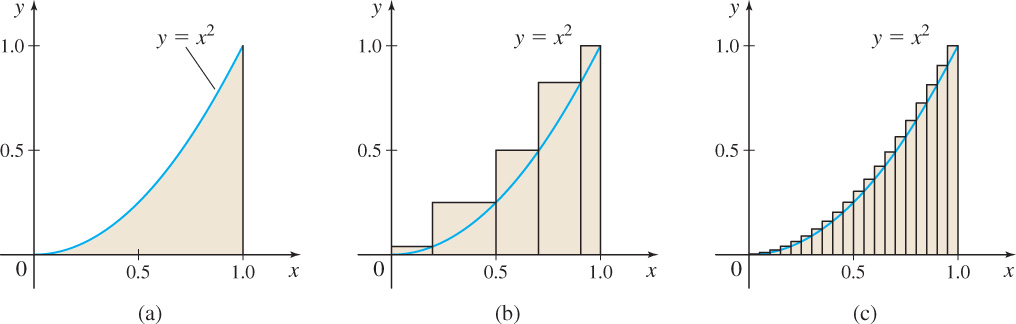
By subdividing the x-axis from 0 to 1 into small segments and drawing a rectangle of height x² above each segment, as in Figure 4(b), we can find the area of each rectangle and add them together. This sum approximates the shaded area in Figure 4(a). The smaller we make the segments of the x-axis and the more rectangles we draw, the better the approximation becomes. See Figure 4(c). This formulation leads to integral calculus, and the study of the integral of a function.

Two Problems—One Subject?

At first, differential calculus (the tangent problem) and integral calculus (the area problem) appear to be different, so why call both of them calculus? The Fundamental Theorem of Calculus establishes that the derivative and the integral are related. In fact, one of Newton’s teachers, Isaac Barrow, recognized that the tangent problem and the area problem are closely related, and that derivatives and integrals are inverses of each other. Both Newton and Leibniz formalized this relationship between derivatives and integrals in the Fundamental Theorem of Calculus.