Question

True or False \(\dfrac{d}{dx}\cos x= \sin x\)

Question

True or False \(\dfrac{d}{dx}\tan x=\)\(\cot x\)

Question

True or False \(\dfrac{d^{2}}{dx^{2}}\sin x=-\sin x\)

Question

True or False \(\dfrac{d}{dx}\sin \dfrac{\pi }{3}=\cos \dfrac{\pi}{3}\)

Question

\(f(x)=x-\sin x\), \(c=\pi\)

Question

\(f(\theta )=2\sin \theta +\cos \theta\), \(c={\dfrac{\pi }{2}}\)

Question

\(f(\theta )={\dfrac{\cos \theta }{1+\sin \theta }}\), \(c=\dfrac{\pi }{3}\)

Question

\(f(x)={\dfrac{\sin x}{1+\cos x}}\), \(c=\dfrac{5\pi }{6}\)

Question

\(y=3\sin \theta -2\cos \theta\)

Question

\(y=4\tan \theta +\sin \theta\)

Question

\(y=\sin x\cos x\)

Question

\(y=\cot x\tan x\)

Question

\(y=t\cos t\)

Question

\(y=t^{2}\tan t\)

Question

\(y=e^{x}\tan x\)

Question

\(y=e^{x}\sec x\)

Question

\(y=\pi \sec u\tan u\)

Question

\(y=\pi u\tan u\)

Question

\(y={\dfrac{\cot x}{x}}\)

Question

\(y={\dfrac{\csc x}{x}}\)

Question

\(y=x^{2}\sin x\)

Question

\(y=t^{2}\tan t\)

Question

\(y=t\tan t-\sqrt{3}\sec t\)

Question

\(y=x\sec x+\sqrt{2}\cot x\)

Question

\(y=\dfrac{\sin \theta }{1-\cos \theta}\)

Question

\(y={\dfrac{x}{\cos x}}\)

Question

\(y={\dfrac{\sin t}{1+t}}\)

Question

\(y={\dfrac{\tan u}{1+u}}\)

Question

\(y=\dfrac{\sin x}{e^{x}}\)

Question

\(y=\dfrac{e^{x}}{\cos x}\)

Question

\(y={\dfrac{\sin \theta +\cos \theta }{\sin \theta -\cos \theta }}\)

Question

\(y={\dfrac{\sin \theta -\cos \theta }{\sin \theta +\cos \theta }}\)

Question

\(y={\dfrac{\sec t}{1+t\sin t}}\)

Question

\(y={\dfrac{\csc t}{1+t\cos t}}\)

Question

\(y=\csc \theta\cot \theta\)

Question

\(y=\tan \theta \cos \theta\)

Question

\(y={\dfrac{1+\tan x}{1-\tan x}}\)

Question

\(y={\dfrac{\csc x-\cot x}{\csc x+\cot x}}\)

Question

\(y=\sin x\)

Question

\(y=\cos x\)

Question

\(y=\tan \theta\)

Question

\(y=\sec \theta \)

Question

\(y=t\sin t\)

Question

\(y=t\cos t\)

Question

\(y=e^{x}\sin x\)

Question

\(y=e^{x}\cos x\)

Question

\(y=2\sin u-3\cos u\)

Question

\(y=3\sin u+4\cos u\)

Question

\(y=a\sin x+b\cos x\)

Question

\(y=a\sec\theta +b\tan \theta \)

Question

\(f(x)=\sin x\) at \((0,0)\)

Question

\(f(x)=\cos x\) at \({\left( \dfrac{\pi }{3},\dfrac{1}{2}\right) }\)

Question

\(f(x)=\tan x\) at \((0,0)\)

Question

\(f(x)=\tan x\) at \({\left( \dfrac{\pi }{4},1\right)}\)

Question

\(f(x)=\sin x+\cos x\) at \({\left( \dfrac{\pi }{4},\sqrt{2}\right)}\)

Question

\(f(x)=\sin x-\cos x\) at \({\left( \dfrac{\pi }{4},0\right) }\)

Question

\(f(x)=2\sin x+\cos x\)

Question

\(f(x)=\cos x-\sin x\)

Question

\(f(x)=\sec x\)

Question

\(f(x)=\csc x\)

Question

\(f(x)=\sin x\)

Question

\(f(\theta )=\cos \theta \)

Question

What is \({\lim\limits_{h\rightarrow 0}\dfrac{\cos \left( { \dfrac{\pi }{2}}+h\right) -\cos {\dfrac{\pi }{2}}}{h}?}\)

Question

What is \(\lim\limits_{h\rightarrow 0}{\dfrac{\sin (\pi +h)-\sin \pi }{h}?}\)

Question

Simple Harmonic Motion The distance \(s\) (in meters) of an object from the origin at time \(t\) (in seconds) is modeled by the function \(s( t) =\dfrac{1}{8}\cos t\).

1. Find the velocity \(v\) of the object.
2. When is the speed of the object at a maximum?
3. Find the acceleration \(a\) of the object.
4. When is the acceleration equal to 0?
5. Graph \(s,\) \(v\), and \(a\) on the same screen.

Question

Simple Harmonic Motion An object attached to a coiled spring is pulled down a distance \(d=\) \(5~{\text{cm}}\) from its equilibrium position and then released as shown in the figure. The motion of the object at time \( t \) seconds is simple harmonic and is modeled by \(d(t) =-5\cos t\).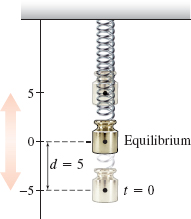

1. As \(t\) varies from 0 to \(2\pi\), how does the length of the spring vary?
2. Find the velocity \(v\) of the object.
3. When is the speed of the object at a maximum?
4. Find the acceleration \(a\) of the object.
5. When is the acceleration equal to 0?
6. Graph \(d,\) \(v\), and \(a\) on the same screen.

Question

Rate of Change A large, 8-ft high decorative mirror is placed on a wood floor and leaned against a wall. The weight of the mirror and the slickness of the floor cause the mirror to slip.

1. If \(\theta \) is the angle between the top of the mirror and the wall, and \(y\) is the distance from the floor to the top of the mirror, what is the rate of change of \(y\) with respect to \(\theta ?\)
2. In feet/radian, how fast is the top of the mirror slipping down the wall when \( \theta =\dfrac{\pi }{4}?\)

Question

Rate of Change The sides of an isosceles triangle are sliding outward. See the figure.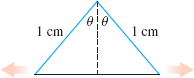

1. Find the rate of change of the area of the triangle with respect to \(\theta\).
2. How fast is the area changing when \(\theta =\dfrac{\pi }{6}?\)

Question

Sea Waves Waves in deep water tend to have the symmetric form of the function \(f(x)=\sin x\). As they approach shore, however, the sea floor creates drag which changes the shape of the wave. The trough of the wave widens and the height of the wave increases, so the top of the wave is no longer symmetric with the trough. This type of wave can be represented by a function such as \[ w(x)=\dfrac{4}{2+\cos x}. \]

Source: http://www.crd.bc.ca/watersheds/protection/geology-processes/waves.htm

1. Graph \(w=w(x)\) for \(0 ≤ x ≤ 4\pi\).
2. What is the maximum and the minimum value of \(w\)?
3. Find the values of \(x\), \(0 < x < 4\pi\), at which \(w'(x)=0\).
4. Evaluate \(w’\) near the peak at \(\pi\), using \(x=\pi-0.1\), and near the trough at \(2\pi\), using \(x=2\pi-0.1\).
5. Explain how these values confirm a non-symmetric wave shape.

Question

Swinging Pendulum A simple pendulum is a small-sized ball swinging from a light string. As it swings, the supporting string makes an angle \(\theta\) with the vertical. See the figure. At an angle \(\theta\), the tension in the string is \(T=\dfrac{W}{\cos \theta }\), where \(W\) is the weight of the swinging ball.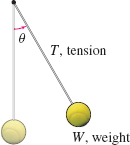

1. Find the rate of change of the tension \(T\) with respect to \(\theta\) when the pendulum is at its highest point (\(\theta =\theta _{\max })\).
2. Find the rate of change of the tension \(T\) with respect to \(\theta\) when the pendulum is at its lowest point.
3. What is the tension at the lowest point?

Question

Restaurant Sales A restaurant in Naples, Florida is very busy during the winter months and extremely slow over the summer. But every year the restaurant grows its sales. Suppose over the next two years, the revenue \(R\), in units of $10,000, is projected to follow the model \[ R=R( t) =\sin t+0.3t+1 \qquad 0 ≤ t ≤ 12 \] where \(t=0\) corresponds to November 1, 2014; \(t=1\) corresponds to January 1, 2015; \(t=2\) corresponds to March 1, 2015; and so on.

1. What is the projected revenue for November 1, 2014; March 1, 2015; September 1, 2015; and January 1, 2016?

   192

2. What is the rate of change of revenue with respect to time?
3. What is the rate of change of revenue with respect to time for January 1, 2016?
4. Graph the revenue function and the derivative function \(R^\prime = R’(t).\)
5. Does the graph of \(R\) support the facts that every year the restaurant grows its sales and that sales are higher during the winter and lower during the summer? Explain.

Question

Polarizing Sunglasses Polarizing sunglasses are filters that only transmit light for which the electric field oscillations are in a specific direction. Light gets polarized naturally by scattering off the molecules in the atmosphere and by reflecting off of many (but not all) types of surfaces. If light of intensity \(I_{0}\) is already polarized in a certain direction, and the transmission direction of the polarizing filter makes an angle with that direction, then the intensity \(I\) of the light after passing through the filter is given by Malus’s Law, \(I( \theta ) =I_{0}\cos ^{2}\theta \).

1. As you rotate a polarizing filter, \(\theta\) changes. Find the rate of change of the light intensity \(I\) with respect to \(\theta \).
2. Find both the intensity \(I(\theta) \) and the rate of change of the intensity with respect to \(\theta \), for the angles \(\theta =0° , 45° \), and \(90°\). (Remember to use radians for \(\theta\).)

Question

If \(y=\sin x\) and \(y^{(n)}\) is the \(n\)th derivative of \(y\) with respect to \(x\) find the smallest positive integer \(n\) for which \(y^{(n)}=y\).

Question

Use the identity \(\sin A-\sin B=2\cos \dfrac{A+B}{2}\sin \dfrac{A-B}{2},\) with \(A=x+h\) and \(B=x\), to prove that \[ \dfrac{d}{dx}\sin x= \lim\limits_{h\rightarrow 0}\dfrac{\sin (x+h)-\sin x}{h}=\cos x \]

Question

Use the definition of a derivative to prove \(\dfrac{d }{dx}\cos x=-\sin x\).

Question

Derivative of \({y=\sec x}\) Use a derivative rule to show that \[ \dfrac{d}{dx}\sec x=\sec x\tan x. \]

Question

Derivative of \(y=csc x\) Use a derivative rule to show that \[ \dfrac{d}{dx}\csc x=-\csc x\cot x. \]

Question

Derivative of \({y=\cot x}\) Use a derivative rule to show that \[ \dfrac{d}{dx}\cot x=-\csc ^{2}x. \]

Question

Let \(f(x)=\cos x\). Show that finding \(f^\prime (0)\) is the same as finding \(\lim\limits_{x\rightarrow 0}{\dfrac{\cos x-1}{x}}\).

Question

Let \(f(x)=\sin x\). Show that finding \(f^\prime (0)\) is the same as finding \(\lim\limits_{x\rightarrow 0}{\dfrac{\sin x}{x}}\).

Question

If \(y=A\sin t+B\cos t\), where \(A\) and \(B\) are constants, show that \(y''+y=0\).

Question

For a differentiable function \(f\), let \(f^{\ast }\) be the function defined by \[ f^{\ast }(x)=\lim\limits_{h\rightarrow 0}\frac{f(x+h)-f(x-h)}{h} \]