2.3 The Derivative of a Polynomial Function; The Derivative of y=ex
163
OBJECTIVES
When you finish this section, you should be able to:
- Differentiate a constant function (p. 163)
- Differentiate a power function (p. 164)
- Differentiate the sum and the difference of two functions (p. 166)
- Differentiate the exponential function \( y\, =\, e^{ x}\) (p. 168)
Finding the derivative of a function from the definition can become tedious, especially if the function \(f\) is complicated. Just as we did for limits, we derive some basic derivative formulas and some properties of derivatives that make finding a derivative simpler.
Before getting started, we introduce other notations commonly used for the derivative of a function \(y=f(x)\). The most common ones are \[ y\prime \qquad \dfrac{dy}{dx} \qquad Df( x) \]
Leibniz notation \(\dfrac{dy}{dx}\) may be written in several equivalent ways as \[ \dfrac{dy}{dx}=\dfrac{d}{dx}y=\dfrac{d}{dx}f( x) \] where \(\dfrac{d}{dx}\) is an instruction to find the derivative (with respect to the independent variable \(x\)) of the function \(y=f( x)\).
In operator notation \(Df( x)\), \(D\) is said to operate on the function, and the result is the derivative of \(f\). To emphasize that the operation is performed with respect to the independent variable \(x\), it is sometimes written \(Df( x) =D_{x}f( x)\).
We use prime notation or Leibniz notation, or sometimes a mixture of the two, depending on which is more convenient. We do not use operator notation in this book.
1 Differentiate a Constant Function
See Figure 19. Since the graph of a constant function \(f( x) =A\) is a horizontal line, the tangent line to \(f\) at any point is also a horizontal line, whose slope is 0. Since the derivative is the slope of the tangent line, the derivative of \(f\) is 0.
THEOREM Derivative of a Constant Function
If \(f\) is the constant function \(f( x) =A\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt] f\prime (x) =0} \]
That is, if \(A\) is a constant, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt]{ \dfrac{d}{dx}A=0}} \]
PROOF
If \(f( x) =A\), then its derivative function is given by \[ \begin{eqnarray*} f' ( x) \underset{\underset{\underset{\color{#0066A7}{\hbox{derivative, form (3)}}}{\color{#0066A7}{\hbox{The definition of a}}}}{\color{#0066A7}{\uparrow }}}{=} \lim\limits_{h\rightarrow 0}\dfrac{f(x+h) -f(x)}{h} \underset{\underset{\underset{\color{#0066A7}{\hbox{\(f( x+h) =A\)}}}{\color{#0066A7}{\hbox{\(f( x) =A\)}}}}{\color{#0066A7}{\uparrow }}}{=} \lim\limits_{h\rightarrow 0}\dfrac{A-A}{h}{\normalsize =0} \\ \end{eqnarray*} \]
IN WORDS
The derivative of a constant is 0.
164
Differentiating a Constant Function
- If \(f(x) =\sqrt{3}\), then \(f' (x) =0\)
- If \(f(x) =-\dfrac{1}{2}\), then \(f' ( x) =0\)
- If \(f(x) =\pi \), then \(\dfrac{d}{dx}\pi =0\)
- If \(f( x) =0\), then \(\dfrac{d}{dx}0=0\)
2 Differentiate a Power Function
Next we take up the derivative of a power function \(f(x) =x^{n}\), where \(n ≥ 1\) is an integer.
When \(n=1\), then \(f(x) =x\) is the identity function and its graph is the line \(y=x\), as shown in Figure 20.
The slope of the line \(y=x\) is 1, so we would expect \(f'( x) =1\).
Proof
\[ f' ( x) =\dfrac{d}{dx}x = \lim\limits_{h\rightarrow 0}\dfrac{f( x+h) -f( x) }{h} \underset{\underset{\color{#0066A7}{f(x) =x,f ( x+h) =x+h}}{\color{#0066A7}{\uparrow}}}{=} \lim\limits_{h\rightarrow 0} \dfrac{( x+h) -x}{h}= \lim\limits_{h\rightarrow 0}\dfrac{h}{h}=1 \]
THEOREM Derivative of \(f(x)=x\)
If \(f(x) =x,\) then \[\bbox[5px, border:1px solid black, #F9F7ED]{f^\prime (x) =\dfrac{d}{dx}x=1} \]
When \(n=2,\) then \(f(x)=x^{2}\) is the square function. The derivative of \(f\) is \[ \begin{eqnarray*} f^\prime (x) &=& \dfrac{d}{dx}x^{2}=\lim\limits_{h\rightarrow 0} \dfrac{( x+h) ^{2}-x^{2}}{h}=\lim\limits_{h\rightarrow 0}\dfrac{ x^{2}+2hx+h^{2}-x^{2}}{h}\\[5pt] &=&\lim\limits_{h\rightarrow 0}\dfrac{h(2x+h)}{h}=\lim\limits_{h\rightarrow 0}( 2x+h) =2x \end{eqnarray*} \]
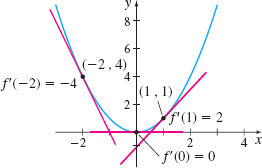
The slope of the tangent line to the graph of \(f(x) =x^{2}\) is different for every number \(x\). Figure 21 shows the graph of \(f\) and several of its tangent lines. Notice that the slope of each tangent line drawn is twice the value of \(x\).
When \(n=3\), then \(f(x) =x^{3}\) is the cube function. The derivative of \(f\) is \[ \begin{eqnarray*} f^\prime ( x) &=&\lim\limits_{h\rightarrow 0}\dfrac{( x+h) ^{3}-x^{3}}{h}=\lim\limits_{h\rightarrow 0}\dfrac{ x^{3}+3x^{2}h+3xh^{2}+h^{3}-x^{3}}{h}\\ &=&\lim\limits_{h\rightarrow 0}\dfrac{ h( 3x^{2}+3xh+h^{2}) }{h}=\lim\limits_{h\rightarrow 0}( 3x^{2}+3xh+h^{2}) =3x^{2} \end{eqnarray*} \]
Notice that the derivative of each of these power functions is another power function, whose degree is 1 less than the degree of the original function and whose coefficient is the degree of the original function. This rule holds for all power functions as the following theorem, called the Simple Power Rule, indicates.
IN WORDS
The derivative of \(x\) raised to an integer power \(n ≥ 1\) is \(n\) times \(x\) raised to the power \(n-1\).
THEOREM Simple Power Rule*
The derivative of the power function \(y=x^{n},\) where \(n ≥ 1\) is an integer, is \[\bbox[5px, border:1px solid black, #F9F7ED]{y^\prime =\dfrac{d}{dx}x^{n}=nx^{n-1}} \]
* \(\dfrac{d}{dx}x^{n}=nx^{n-1}\) is true not only for positive integers \(n\) but also for any real number \(n\). But the proof requires future results. As these are developed, we will expand the Power Rule to include an ever-widening set of numbers until we arrive at the fact it is true when \(n\) is a real number.
165
NEED TO REVIEW?
The Binomial Theorem is discussed in Appendix A.5, pp. A-42 to A-43.
Proof
If \(f(x) =x^{n}\) and \(n\) is a positive integer, then \(f(x+h) =( x+h) ^{n}\). We use the Binomial Theorem to expand \((x+h) ^{n}.\) Then \[ \begin{eqnarray*} f(x+h) =(x+h) ^{n}&=&x^{n}+nx^{n-1}h+\dfrac{n(n-1)}{2}x^{n-2}h^{2} +\dfrac{n(n-1) (n-2) }{6}x^{n-3}h^{3}+\cdots+nxh^{n-1}+h^{n} \end{eqnarray*} \]
and \[ \begin{eqnarray*} f^\prime(x) &=&\lim\limits_{h\rightarrow 0}\dfrac{f( x+h) -f( x) }{h} \\[6pt] &=&\lim\limits_{h\rightarrow 0}\dfrac{\left[ x^{n}+nx^{n-1}h+\dfrac{n\left( n-1\right) }{2}x^{n-2}h^{2}+\dfrac{n( n-1) ( n-2) }{6} x^{n-3}h^{3}+\cdots+nxh^{n-1}+h^{n}\right] -x^{n}}{h} \\[6pt] &=&\lim\limits_{h\rightarrow 0}\dfrac{\vphantom{\left[ x^{n}+nx^{n-1}h+\dfrac{n\left( n-1\right) }{2}x^{n-2}h^{2}+\dfrac{n( n-1) ( n-2) }{6} x^{n-3}h^{3}+\cdots+nxh^{n-1}+h^{n}\right] }nx^{n-1}h+\dfrac{n( n-1) }{2 }x^{n-2}h^{2}+\dfrac{n( n-1) ( n-2) }{6} x^{n-3}h^{3}+\cdots+nxh^{n-1}+h^{n}}{h} & {\color{#0066A7}{\hbox{Simplify.}}}\\[6pt] &=&\lim\limits_{h\rightarrow 0}\dfrac{h\!\left[ nx^{n-1}+\dfrac{n( n-1) }{2}x^{n-2}h+\dfrac{n( n-1) ( n-2) }{6} x^{n-3}h^{2}+\cdots+nxh^{n-2}+h^{n-1}\!\right]\!\! }{h} & {\color{#0066A7}{\hbox{Factor \(h\) in the numerator.}}} \\[6pt] &=&\lim\limits_{h\rightarrow 0}\left[ nx^{n-1}+\dfrac{n( n-1) }{2} x^{n-2}h+\dfrac{n( n-1) ( n-2) }{6} x^{n-3}h^{2}+\cdots+nxh^{n-2}+h^{n-1}\right] & {\color{#0066A7}{\hbox{Divide out the common $h$.}}} \\[6pt] &=&nx^{n-1} & {\color{#0066A7}{\hbox{Take the limit. Only the first term remains.}}} \end{eqnarray*} \]
Differentiating a Power Function
- \(\dfrac{d}{dx}x^{5}=5x^{4}\)
- If \(g(x) =x^{10}\), then \(g^\prime (x) =10x^{9}\).
NOW WORK
Problem 1.
But what if we want to find the derivative of the function \(f(x) =ax^{n}\) when \(a\neq 1\)? The next theorem, called the Constant Multiple Rule, provides a way.
IN WORDS
The derivative of a constant times a differentiable function \(f\) equals the constant times the derivative of \(f\).
THEOREM Constant Multiple Rule
If a function \(f\) is differentiable and \(k\) is a constant, then \( F(x) =kf(x)\) is a function that is differentiable and \[\bbox[5px, border:1px solid black, #F9F7ED]{F' ( x) =k f^\prime ( x) } \]
Proof
We use the definition of derivative. \[ \begin{eqnarray*} F' (x) &=&\lim\limits_{h\rightarrow 0}\dfrac{F(x+h) - F(x) }{h}=\lim\limits_{h\rightarrow 0}\dfrac{ kf(x+h) - kf(x) }{h}\\[5pt] &=&\lim\limits_{h\rightarrow 0}\dfrac{k\left[ f(x+h) - f(x) \right] }{h} =k\cdot \lim\limits_{h\rightarrow 0}\dfrac{f(x+h) - f(x)}{h}=k\cdot f^\prime (x) \end{eqnarray*} \]
Using Leibniz notation, the Constant Multiple Rule takes the form \[\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{d}{dx}[ kf(x) ] =k\left[ \dfrac{d}{dx}f(x) \right]} \]
A change in the symbol used for the independent variable does not affect the derivative formula. For example, \(\dfrac{d}{dt}t^{\,2}=2t\) and \(\dfrac{d}{du}u^{5}=5u^{4}.\)
166
Differentiating a Constant Times a Power Function
Find the derivative of each power function:
- \(f( x) =5x^{3}\)
- \(g( u) =-\dfrac{1}{2}u^{2} \)
- \(u( x) =\pi ^{4}x^{3}\)
Solution Notice that each of these functions involves the product of a constant and a power function. So, we use the Constant Multiple Rule followed by the Simple Power Rule.
- \(f( x) =5\cdot x^{3},\) so \(f^\prime ( x) =5\left[ \dfrac{d}{dx}x^{3}\right] =5\cdot 3x^{2}=15x^{2}\)
- \(g( u) =-\dfrac{1}{2}\cdot u^{2}\), so \(g^\prime ( u) =-\dfrac{1}{2}\cdot \dfrac{d}{du}u^{2}=-\dfrac{1}{2}\cdot 2u^{1}=-u\)
- \(u( x) =\pi ^{4}x^{3}, \)so \(u' ( x)\underset{\underset{\color{#0066A7}{\pi~\text{is a constant}}}{\color{#0066A7}{{\uparrow }}}}{=} \pi ^{4}\cdot \dfrac{d}{dx}x^{3}=\pi ^{4}\cdot 3x^{2}=3\pi ^{4}x^{2}\)
NOW WORK
Problem 31.
3 Differentiate the Sum and the Difference of Two Functions
We can find the derivative of a function that is the sum of two functions whose derivatives are known by adding the derivatives of each function.
IN WORDS
The derivative of the sum of two differentiable functions equals the sum of their derivatives. That is, \( ( f+g ) ' =f^\prime +g^\prime \).
THEOREM Sum Rule
If two functions \(f\) and \(g\) are differentiable and if \(F( x) =f( x) +g( x) ,\) then \(F\) is differentiable and \[\bbox[5px, border:1px solid black, #F9F7ED]{ F^\prime( x) = (f^\prime (x) + g^\prime (x)} \]
Proof
When \(F( x) =f( x) +g( x) \), then \[ \begin{eqnarray*} F( x+h) -F( x) &=&[ f( x+h) +g( x+h) ] -[ f( x) +g( x) ]\\ &=&[f( x+h) -f( x) ] +[ g( x+h)-g( x) ] \end{eqnarray*} \]
So, the derivative of \(F\) is \[ \begin{eqnarray*} F' ( x) &=&\lim\limits_{h\rightarrow 0}\dfrac{[ f( x+h) -f( x) ] +[ g( x+h) -g( x) ] }{h}\\ &=&\lim\limits_{h\rightarrow 0}\dfrac{f( x+h) -f( x) }{h}+\lim\limits_{h\rightarrow 0}\dfrac{g( x+h) -g( x) }{h} \underset{{\color{#0066A7}{\hbox{ the sum of the limits.}}}}{\color{#0066A7}{\hbox{The limit of a sum is}}}\\ &=&f^\prime ( x) +g^\prime ( x) \end{eqnarray*} \]
In Leibniz notation, the Sum Rule takes the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt] {\frac {d}{dx}[f(x) + g(x)] = \frac {d}{dx} f(x) + \frac {d}{dx} g(x)}} \]
Differentiating the Sum of Two Functions
Find the derivative of \(f( x) =3x^{2}+8\).
Solution Here, \(f\) is the sum of \(3x^{2}\) and \(8\). So, we begin by using the Sum Rule. \[ \begin{eqnarray*} &&f^\prime ( x) =\dfrac{d}{dx} ( 3x^{2}+8 ) \underset{\underset{{\color{#0066A7}{\hbox{ Sum Rule}}}}{\color{#0066A7}{\uparrow}}}{=} \dfrac{d}{dx} ( 3x^{2} ) + \dfrac{d}{dx}8 \underset{\underset{\underset{{\color{#0066A7}{\hbox{ Multiple Rule}}}}{\color{#0066A7}{\hbox{ Constant}}}}{\color{#0066A7}{\uparrow }}}{=} 3\dfrac{d}{dx}x^{2}+0 \underset{\underset{\underset{{\color{#0066A7}{\hbox{ Power Rule}}}}{\color{#0066A7}{\hbox{ Simple}}}}{\color{#0066A7}{\uparrow}}}{=} 3\cdot 2x=6x \end{eqnarray*} \]
NOW WORK
Problem 7.
167
IN WORDS
The derivative of the difference of two differentiable functions is the difference of their derivatives. That is, \(( f-g )' =f^\prime -g' \).
THEOREM Difference Rule
If the functions \(f\) and \(g\) are differentiable and if \(F( x) =f( x) -g( x) ,\) then \(F\) is differentiable, and \(F' ( x) =f^\prime ( x)-g^\prime ( x) \), \[\bbox[5px, border:1px solid black, #F9F7ED]{\frac {d}{dx}[f(x) - g(x)] = \frac {d}{dx} f(x) - \frac {d}{dx} g(x)} \]
The proof of the Difference Rule is left as an exercise. (See Problem 78.)
The Sum and Difference Rules extend to sums (or differences) of more than two functions. That is, if the functions \(f_{1},\) \(f_{2},\ldots,\) \(f_{n}\) are all differentiable, and \(a_{1},a_{2}, \ldots , a_{n}\) are constants, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\frac{d}{dx}[ a_{1}f_{1}( x) +a_{2}f_{2}( x) +\cdots+a_{n}f_{n}( x) ] =a_{1} \dfrac{d}{dx}f_{1}( x) +a_{2}\dfrac{d}{dx}f_{2}( x) +\cdots+a_{n}\dfrac{d}{dx}f_{n}( x)} \]
Combining the rules for finding the derivative of a constant, a power function, and a sum or difference allows us to differentiate any polynomial function.
Differentiating a Polynomial Function
- Find the derivative of \(f( x) =2x^{4}-6x^{2}+2x-3\).
- What is \(f^\prime (2) ?\)
- Find the slope of the tangent line to the graph of \(f\) at the point \( ( 1,-5)\).
- Find an equation of the tangent line to the graph of \(f\) at the point \(( 1,-5)\).
 Use graphing technology to graph \(f\) and the tangent line to the graph of \(f\) at the point \((1, -5)\) on the same screen.
Use graphing technology to graph \(f\) and the tangent line to the graph of \(f\) at the point \((1, -5)\) on the same screen.
Solution (a) \[ \begin{eqnarray*} f^\prime ( x) &=&\dfrac{d}{dx}( 2x^{4}-6x^{2}+2x-3) {=} \dfrac{d}{dx}( 2x^{4}) -\dfrac{d}{dx}( 6x^{2}) +\dfrac{d}{dx} ( 2x) -\dfrac{d}{dx}3 \\[-6.4pt] &&\hspace{4.85pc}\underset{{\color{#0066A7}{\text{Sum & Difference Rules}}}}{\color{#0066A7}{\uparrow }}\\[-6.4pt] &{=}& 2\cdot \dfrac{d}{dx}x^{4}-6\cdot \dfrac{d}{dx}x^{2}+2\cdot \dfrac{d}{dx}x-0 \\[-6.4pt] &&\hspace{-3.15pc}\underset{{\color{#0066A7}{\text{Constant Multiple Rule}}}}{\color{#0066A7}{\uparrow }}\\ &{=}& 2\cdot 4x^{3}-6\cdot 2x+2\cdot 1 {=} 8x^{3}-12x+2\\[-6.4pt] &&\hspace{-3.7pc}\hspace{1pc}\underset{\color{#0066A7}{\text{Simple Power Rule}}}{\color{#0066A7}{\uparrow }}\hspace{4.4pc}\underset{{\color{#0066A7}{\text{Simplify}}}}{\color{#0066A7}{\uparrow }} \end{eqnarray*} \]
(b) \(f^\prime (2) =8( 2)^{3} -12(2) +2=64-24+2=42\).
(c) The slope of the tangent line at the point (1, −5) equals \(f′(1)\). \[ f^\prime (1) =8( 1)^{3} -12(1) +2=8-12+2=-2 \]
(d) We use the point-slope form of an equation of a line to find an equation of the tangent line at \((1,-5)\). \[ \begin{eqnarray*} y-( -5) &=&-2( x-1) \\ y &=&-2( x-1) -5=-2x+2-5=-2x-3 \end{eqnarray*} \]
The line \(y=-2x-3\) is tangent to the graph of \(f( x) =2x^{4}-6x^{2}+2x-3\) at the point \((1, -5)\).
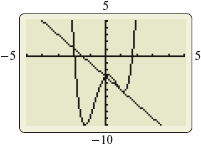
(e) The graphs of \(f\) and the tangent line to \(f\) at \((1, -5)\) are shown in Figure 22.
NOW WORK
Problem 33.
In some applications, we need to solve equations or inequalities involving the derivative of a function.
168
Solving Equations and Inequalities Involving Derivatives
- Find the points on the graph of \(f( x) =4x^{3}-12x^{2}+2\), where \(f\) has a horizontal tangent line.
- Where is \(f^\prime (x)>0\)? Where is \(f'(x) < 0\)?
Solution (a) The slope of a horizontal tangent line is 0. Since the derivative of \(f\) equals the slope of the tangent line, we need to find the numbers \(x\) for which \(f^\prime ( x) =0\). \[ \begin{eqnarray*} f^\prime ( x) &=& 12x^{2}-24x = 12x (x-2) \\ 12x ( x-2 ) &=& 0 & {\color{#0066A7}{\hbox{\(f^{\,\prime} ( x ) =0.\)}}} \\ x &=&0\hbox{ or }x=2 & {\color{#0066A7}{\hbox{Solve.}}} \end{eqnarray*} \]
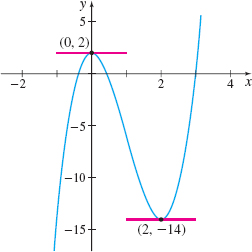
At the points \(( 0,f( 0) ) =( 0,2)\) and \(( 2,f(2) ) =( 2,-14)\), the graph of the function \(f( x) =4x^{3}-12x^{2}+2\) has a horizontal tangent line.
(b) Since \(f^\prime(x)=12x (x-2)\) and we want to solve the inequalities \(f^\prime(x)>0\) and \(f^\prime(x) < 0\), we use the zeros of \(f^\prime\), 0 and 2, and form a table using the intervals (\(-\infty,0\)), (0,2), and (\(2, \infty)\).
| Interval | \((-\infty,0)\) | (\(0,2\)) | (\(2, \infty)\) |
| Sign of \(f'(x) = 12x(x-2)\) | Positive | Negative | Positive |
We conclude \(f'(x)>0\) on \((-\infty,0) \cup (2,\infty)\) and \(f'(x) < 0\) on \((0,2)\),
Figure 23 shows the graph of \(f\).
NOW WORK
Problem 37.
4 Differentiate the Exponential Function y=ex
None of the differentiation rules developed so far allows us to find the derivative of an exponential function. To differentiate \(f( x)=a^{x}\), we return to the definition of a derivative.
NEED TO REVIEW?
Exponential functions are discussed in Section P.5, on pp. 38-42.
We begin by making some general observations about the derivative of \(f( x) =a^{x}\), \(a>0\) and \(a\neq 1\). We will then use these observations to find the derivative of the exponential function \(y=e^{x}\).
Suppose \(f( x) =a^{x}\), where \(a>0\) and \(a\neq 1\). The derivative of \(f\) is \[ \begin{eqnarray*} f^\prime ( x) =\lim\limits_{h\rightarrow 0}\dfrac{f( x+h) -f( x) }{h}=\lim\limits_{h\rightarrow 0}\dfrac{ a^{x+h}-a^{x}}{h} \underset{\underset{\color{#0066A7}{\hbox{\(a^{x+h}=a^x\cdot a^h\)}}}{\color{#0066A7}{\uparrow}}}{=} \lim\limits_{h\rightarrow 0} \dfrac{a^x \cdot a^h - a^x}{h} \\ \end{eqnarray*} \]
\[ \begin{eqnarray*} \underset{\underset{\color{#0066A7}{\hbox{Factor out \({a}^{x}.\)}}}{\color{#0066A7}{\uparrow }}}{=} \lim\limits_{h\rightarrow 0}\left[ a^{x}\cdot \dfrac{a^{h}-1}{h}\right] =a^{x}\cdot \lim\limits_{h\rightarrow 0}\dfrac{a^{h}-1}{h}\\[-10pt] \end{eqnarray*} \]
provided \(\lim\limits_{h\rightarrow 0}\dfrac{a^{h}-1}{h}\) exists.
Three observations about the derivative are significant:
- \(f^\prime ( 0) =a^{0}\lim\limits_{h\rightarrow 0}\dfrac{a^{h}-1}{h}=\lim\limits_{h\rightarrow 0}\dfrac{a^{h}-1}{h}.\)
- \(f^\prime ( x)\) is a multiple of \(a^{x}\). In fact, \(\dfrac{d}{dx}a^{x}=f^\prime ( 0) \cdot a^{x}\).
- If \(f^\prime ( 0)\) exists, then \(f^\prime ( x)\) exists, and the domain of \(f^\prime\) is the same as that of \(f( x) =a^{x}\), all real numbers.
169
NEED TO REVIEW?
The number \(e\) is discussed in Section P.5, pp. 41-42.
The slope of the tangent line to the graph of \(f( x) =a^{x}\) at the point \(( 0,1)\) is \(f^\prime ( 0) =\lim\limits_{h\rightarrow 0}\dfrac{a^{h}-1}{h}\), and the value of this limit depends on the base \(a\). In Section P.5, the number \(e\) was defined as that number for which the slope of the tangent line to the graph of \(y=a^{x}\) at the point (0, 1) equals 1. That is, the number \(e\) has the property that \[\bbox[5px, border:1px solid black, #F9F7ED]{\lim\limits_{h\rightarrow 0}\dfrac{e^{h}-1}{h}=1} \]
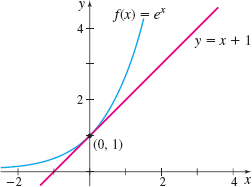
In other words, if \(f( x) =e^{x}\), then \(f^\prime ( 0) =1\). Figure 24 shows \(f( x) =e^{x}\) and the tangent line \(y=x+1\) with slope 1 at the point (0,1).
Since \(\dfrac{d}{dx}a^{x}=f^\prime ( 0) \cdot a^{x}\), if \(f( x) =e^{x}\), then \(\dfrac{d}{dx}e^{x}=f^\prime ( 0) \cdot e^{x}=1\cdot e^{x}=e^{x}\).
THEOREM Derivative of the Exponential Function \(y=e^{x}\)
The derivative of the exponential function \(y=e^{x}\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{y^\prime =\dfrac{d}{dx}e^{x}=e^{x}} \tag{1} \]

Differentiating an Expression Involving \(y=e^{x}\)
Find the derivative of \(f( x) =4e^{x}+x^{3}\).
Solution The function \(f\) is the sum of \(4e^{x}\) and \(x^{3}\). Then \[ \begin{eqnarray*} f^\prime (x) &=&\dfrac{d}{dx}(4e^{x}+x^{3}) {=} \dfrac{d}{dx}(4e^{x})+\dfrac{d}{dx}x^{3}{=}4\dfrac{d}{dx}e^{x}+3x^{2}{=}4e^{x}+3x^{2}\\[-6.4pt] &&\hspace{3.25pc}\underset{\color{#0066A7}{\scriptsize \hbox{Sum Rule}}}{\color{#0066A7}{\uparrow }}\hspace{1.9pc}\underset{\underset{\color{#0066A7}{\scriptsize \hbox{Simple Power Rule}}}{\color{#0066A7}{\scriptsize \hbox{Constant Multiple Rule}}}}{\color{#0066A7}{\uparrow }}\hspace{1.0pc}\underset{\color{#0066A7}{\scriptsize \hbox{Use (1)}.}}{\color{#0066A7}{\uparrow }} \end{eqnarray*} \]
NOW WORK
Problem 25.
Now we have the formula \(\dfrac{d}{dx}e^{x}=e^{x}\). To find the derivative of \(f( x) =a^{x}\), where \(a>0\) and \(a\neq 1\), requires more information and is taken up in Chapter 3.