Question

\(\dfrac{d}{dx}\pi ^{2}\)=_____; \(\dfrac{d}{dx}x^{3}\)=_____.

Question

When \(n\) is a positive integer, the Simple Power Rule states that \(\dfrac{d}{dx}x^{n}\)= _____.

Question

True or False The derivative of a power function of degree greater than 1 is also a power function.

Question

If \(k\) is a constant and \(f\) is a differentiable function, then \(\dfrac{d}{dx}[ kf( x) ]\) = _____.

Question

The derivative of \(f( x) =e^{x}\) is _____.

Question

True or False The derivative of an exponential function \(f( x) =a^{x}\), where \(a>0\) and \(a\neq 1\), is always a constant multiple of \(a^{x}\).

Question

\(f(x)=3x+\sqrt{2}\)

Question

\(f(x)=5x-\pi\)

Question

\(f(x)=x^{2}+3x+4\)

Question

\(f(x)=4x^{4}+2x^{2}-2\)

Question

\(f(u)=8u^{5}-5u+1\)

Question

\(f(u)=9u^{3}-2u^{2}+4u+4\)

Question

\(f(s)=as^{3}+\dfrac{3}{2}s^{2}\)

Question

\(f(s)=4-\pi s^{2}\)

Question

\(f(t)={\dfrac{1}{3}}(t^{5}-8)\)

Question

\(f(x)=\dfrac{1}{5}(x^{7}-3x^{2}+2)\)

Question

\(f(t)={\dfrac{t^{3}+2}{5}}\)

Question

\(f(x)={\dfrac{x^{7}-5x}{9}}\)

Question

\(f(x)={\dfrac{x^{3}+2x+1}{7}}\)

Question

\(f(x)={\dfrac{1}{a}}(ax^{2}+bx+c)\)

170

Question

\(f(x)=ax^{2}+bx+c\)

Question

\(f(x)=ax^{3}+bx^{2}+cx+d\)

Question

\(f( x) =4e^{x}\)

Question

\(f( x) =-\dfrac{1}{2}e^{x}\)

Question

\(f ( u ) =5u^{2}-2e^{u}\)

Question

\(f ( u ) =3e^{u}+10\)

Question

\(\dfrac{d}{dt}\left( \sqrt{3}t+\dfrac{1}{2}\right)\)

Question

\({\dfrac{d}{dt}\left( \dfrac{2t^{4}-5}{8}\right) }\)

Question

\({\dfrac{dA}{dR}}\) if \(A( R) =\pi R^{2}\)

Question

\({\dfrac{dC}{dR}}\) if \(C=2\pi R\)

Question

\({\dfrac{dV}{dr}}\) if \(V=\dfrac{4}{3}\pi r^{3}\)

Question

\({\dfrac{dP}{dT}}\) if \(P=0.2T\)

Question

\(f(x)=x^{3}+3x-1\) at \((0,-1)\)

Question

\(f(x)=x^{4}+2x-\) 1 at \((1,2)\)

Question

\(f( x) =e^{x}+5x\) at \(( 0,1)\)

Question

\(f( x) =4-e^{x}\) at \(( 0,3)\)

Question

\(f(x)=3x^{2}-12x+4\)

Question

\(f(x)=x^{2}+4x-3\)

Question

\(f( x) =x+e^{x}\)

Question

\(f( x) =2e^{x}-1\)

Question

\(f(x)=x^{3}-3x+2\)

Question

\(f( x) =x^{4}-4x^{3}\)

Question

Rectilinear Motion At \(t\) seconds, an object in rectilinear motion is \(s\) meters from the origin, where \(s( t) =t^{3}-t+1\). Find the velocity of the object at \(t=0\) and at \(t=5\).

Question

Rectilinear Motion At \(t\) seconds, an object in rectilinear motion is \(s\) meters from the origin, where \(s( t)=t^{4}-t^{3}+1\). Find the velocity of the object at \(t=0\) and at \(t=1\).

Question

\(s(t)=2-5t+t^{2}\)

Question

\(s(t)=t^{3}-\dfrac{9}{2}t^{2}+6t+4\)

Question

Let \(u( x) =f( x) +g( x)\) and \(v( x) =f( x) -g( x)\).

1. \(u^\prime ( 0) \)
2. \(u^\prime (4) \)
3. \(v^\prime ( -2) \)
4. \(v^\prime (6) \)
5. \(3u^\prime (5) \)
6. \(-2v^\prime (3) \)

Question

Let \(F( t) =f( t) +g( t)\) and \(G( t) =g( t) -f( t) \).

1. \(F' ( 0) \)
2. \(F' ( 3) \)
3. \(F' ( -4) \)
4. \(G' ( -2) \)
5. \(G' ( -1) \)
6. \(G' ( 6) \)

Question

\(f( x) =( 2x-1) ^{3}\)

Question

\(f( x) =( x^{2}+x) ^{4}\)

Question

\({\lim\limits_{h\rightarrow 0}\dfrac{5\left( \dfrac{1}{2}+h\right) ^{8}-5\left( \dfrac{1}{2}\right) ^{8}}{h}}\)

Question

\({\lim\limits_{h\rightarrow 0}\dfrac{6(2+h)^{5}-6(2)^{5}}{h}}\)

Question

\(\lim\limits_{h\rightarrow 0}\dfrac{\sqrt{3}(8+h) ^{5}-\sqrt{3}( 8) ^{5}}{h}\)

Question

\(\lim\limits_{h\rightarrow 0}\dfrac{\pi ( 1+h)^{10}-\pi }{h}\)

Question

\(\lim\limits_{h\rightarrow 0}\dfrac{a( x+h) ^{3}-ax^{3}}{h}\)

Question

\(\lim\limits_{h\rightarrow 0}\dfrac{b( x+h)^{n}-bx^{n}}{h}\)

Question

\({f(x)=3x^{2}-x}\); \({L}\): \({y=5x}\)

Question

\({f(x)=2x^{3}+1}\); \({L}\): \({y=6x-1}\)

Question

\(f( x) =e^{x}\); \(L\): \(y-x-5=0\)

Question

\(f( x) =-2e^{x}\); \({L}\): \(y+2x-8=0\)

Question

\(f(x)=\dfrac{1}{3}x^{3}-x^{2}\); \({L}\): \({y=3x-2}\)

Question

\({f(x)=x^{3}-x}\); \(L\): \({x+y=0}\)

171

Question

Tangent Lines Let \(f(x)=4x^{3}-3x-1\).

1. Find an equation of the tangent line to the graph of \(f\) at \(x=2\).
2. Find the coordinates of any points on the graph of \(f\) where the tangent line is parallel to \(y=x+12\).
3. Find an equation of the tangent line to the graph of \(f\) at any points found in (b).
4. Graph \(f\), the tangent line found in (a), the line \(y=x+12\), and any tangent lines found in (c) on the same screen.

Question

Tangent Lines Let \(f(x)=x^{3}+2x^{2}+x-1\).

1. Find an equation of the tangent line to the graph of \(f\) at \(x=0\).
2. Find the coordinates of any points on the graph of \(f\) where the tangent line is parallel to \(y=3x-2\).
3. Find an equation of the tangent line to the graph of \(f\) at any points found in (b).
4. Graph \(f\), the tangent line found in (a), the line \(y=3x-2\), and any tangent lines found in (c) on the same screen.

Question

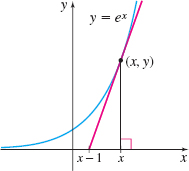
Tangent Line Show that the line perpendicular to the \(x\)-axis and containing the point \((x,y)\) on the graph of \(y=e^{x}\) and the tangent line to the graph of \(y=e^{x}\) at the point \((x,y)\) intersect the \(x\)-axis 1 unit apart. See the figure.

Question

Tangent Line Show that the tangent line to the graph of \(y=x^{n}\) at \((1,1)\) has \(y\)-intercept \(1-n\).

Question

Tangent Lines If \(n\) is an odd positive integer, show that the tangent lines to the graph of \(y=x^{n}\) at \((1,1)\) and at \((-1,-1)\) are parallel.

Question

Tangent Line If the line \(3x-4y=0\) is tangent to the graph of \(y=x^{3}+k\) in the first quadrant, find \(k\).

Question

Tangent Line Find the constants \(a,b\), and \(c\) so that the graph of \(y=ax^{2}+bx+c\) contains the point \((-1,1)\) and is tangent to the line \(y=2x\) at \((0,0)\).

Question

Tangent Line Let \(T\) be the line tangent to the graph of \(y=x^{3}\) at the point \(\left(\dfrac{1}{2},\dfrac{1}{8}\right)\). At what other point \(Q\) on the graph of \(y=x^3\) does the line \(T\) intersect the graph? What is the slope of the tangent line at \(Q\)?

Question

Military Tactics A dive bomber is flying from right to left along the graph of \(y=x^{2}\). When a rocket bomb is released, it follows a path that is approximately along the tangent line. Where should the pilot release the bomb if the target is at \((1,0)\)?

Question

Military Tactics Answer the question in Problem 71 if the plane is flying from right to left along the graph of \(y=x^{3}\).

Question

Fluid Dynamics The velocity \(v\) of a liquid flowing through a cylindrical tube is given by the Hagen–Poiseuille equation \(v=k(R^{2}-r^{2})\), where \(R\) is the radius of the tube, \(k\) is a constant that depends on the length of the tube and the velocity of the liquid at its ends, and \(r\) is the variable distance of the liquid from the center of the tube.

1. Find the rate of change of \(v\) with respect to \(r\) at the center of the tube.
2. What is the rate of change halfway from the center to the wall of the tube?
3. What is the rate of change at the wall of the tube?

Question

Rate of Change Water is leaking out of a swimming pool that measures 20 ft by 40 ft by 6 ft. The amount of water in the pool at a time \(t\) is \(W( t) =35{,}000-20t^{2}\) gallons, where \(t\) equals the number of hours since the pool was last filled. At what rate is the water leaking when \(t=2{h}\)?

Question

Luminosity of the Sun The luminosity \(L\) of a star is the rate at which it radiates energy. This rate depends on the temperature \(T\) and surface area \(A\) of the star’s photosphere (the gaseous surface that emits the light). Luminosity is modeled by the equation \(L=\sigma AT^{4}\), where \(\sigma\) is a constant known as the Stefan–Boltzmann constant, and \(T\) is expressed in the absolute (Kelvin) scale for which 0 K is absolute zero. As with most stars, the Sun’s temperature has gradually increased over the 6 billion years of its existence, causing its luminosity to slowly increase.

1. Find the rate at which the Sun’s luminosity changes with respect to the temperature of its photosphere. Assume that the surface area \(A\) remains constant.
2. Find the rate of change at the present time. The temperature of the photosphere is presently 5800 K (\(10{,}000{^{\circ}{\rm F}}\)), the radius of the photosphere is \(r=6.96\times 10^{8}{m}\), and \(\sigma =5.67\times 10^{-8}\dfrac{{W}}{{m}^{2}{K}^{4}}\).
3. Assuming that the rate found in (b) remains constant, how much would the luminosity change if its photosphere temperature increased by 1 K (1 °C or 1.8 °F)? Compare this change to the present luminosity of the Sun.

Question

Medicine: Poiseuille’s Equation The French physician Poiseuille discovered that the volume \(V\) of blood (in cubic centimeters per unit time) flowing through an artery with inner radius \(R\) (in centimeters) can be modeled by \[ V( R) =kR^{4} \]

where \(k=\dfrac{\pi }{8\nu l}\) is constant (here, \(\nu\) represents the viscosity of blood and \(l\) is the length of the artery).

1. Find the rate of change of the volume \(V\) of blood flowing through the artery with respect to the radius \(R\).
2. Find the rate of change when \(R=0.03\) and when \(R=0.04\).
3. If the radius of a partially clogged artery is increased from 0.03 cm to 0.04 cm, estimate the effect on the rate of change of the volume \(V\) with respect to \(R\) of the blood flowing through the enlarged artery.
4. How do you interpret the results found in (b) and (c)?

172

Question

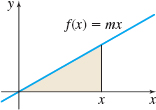
Derivative of the Area Let \(f(x)=mx\), \(m>0\). Let \(F(x)\), \(x>0\), be defined as the area of the shaded region in the figure. Find \(F^{\prime }(x)\).

Question

The Difference Rule Prove that if \(f\) and \(g\) are differentiable functions and if \(F(x)=f(x)-g(x)\), then \(F' (x)=f^\prime(x) -g^\prime (x)\).

Question

Simple Power Rule Let \(f(x)=x^{n}\), where \(n\) is a positive integer. Use a factoring principle to show that \[ f^\prime ( c) =\lim\limits_{x\rightarrow c}\dfrac{f( x) -f( c) }{x-c} =nc^{n-1}. \]

Normal Lines Problems 80-87 involve the following discussion.

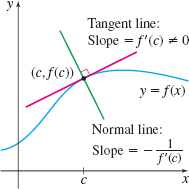
The normal line to the graph of a function \(f\) at a point \((c,f(c))\) is the line through \((c,f(c))\) perpendicular to the tangent line to the graph of \(f\) at \((c,f(c))\). See the figure. If \(f\) is a function whose derivative at \(c\) is \(f^{\prime }(c)\neq 0\), the slope of the normal line to the graph of \(f\) at \((c,f(c))\) is \(-\dfrac{1}{f^\prime (c)}\). Then an equation of the normal line to the graph of \(f\) at \((c,f(c))\) is \(y-f(c)=-\dfrac{1}{f^\prime (c)} (x-c)\).

Question

\(f(x)=x^{2}+1\) at \((1,2)\)

Question

\(f(x)=x^{2}-1\) at \((-1,0)\)

Question

\(f(x)=x^{2}-2x\) at \((-1,3)\)

Question

\(f(x)=2x^{2}+x\) at \((1,3)\)

Question

\(f(x)=\dfrac{1}{x}\) at \((1,1)\)

Question

\(f(x)=\sqrt{x}\) at \((4,2)\)

Question

Normal Lines For what nonnegative number \(b\) is the line given by \(y=-\dfrac{1}{3}x+b\) normal to the graph of \(y=x^{3}\)?

Question

Normal Lines Let \(N\) be the line normal to the graph of \(y=x^{2}\) at the point \((-2,4)\). At what other point \(Q\) does \(N\) meet the graph?

Question

Tangent Line Find \(a,b,c,d\) so that the tangent line to the graph of the cubic \(y=ax^{3}+bx^{2}+cx+d\) at the point \((1,0)\) is \(y=3x-3\) and at the point \((2,9)\) is \(y=18x-27\).

Question

Tangent Line Find the fourth degree polynomial that contains the origin and to which the line \(x+2y=14\) is tangent at both \(x=4\) and \(x=-2\).

Question

Tangent Lines Find equations for all the lines containing the point \(\left( 1,4\right)\) that are tangent to the graph of \(y=x^{3}-10x^{2}+6x-2\). At what points do each of the tangent lines touch the graph?

Question

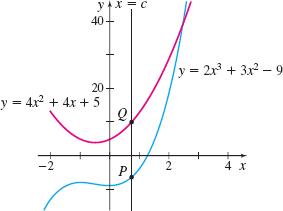
The line \(x=c\), where \(c>0\), intersects the cubic \(y=2x^{3}+3x^{2}-9\) at the point \(P\) and intersects the parabola \(y=4x^{2}+4x+5\) at the point \(Q\), as shown in the figure below.

1. If the line tangent to the cubic at the point \(P\) is parallel to the line tangent to the parabola at the point \(Q\), find the number \(c\).
2. Write an equation for each of the two tangent lines described in (a).

Question

\(f(x)=Ax^{2}+B\), \(A>0\).

1. Find \(c\), \(c>0\), in terms of \(A\) so that the tangent lines to the graph of \(f\) at \((c,f(c))\) and \((-c,f(-c))\) are perpendicular.
2. Find the slopes of the tangent lines in (a).
3. Find the coordinates, in terms of \(A\) and \(B\), of the point of intersection of the tangent lines in (a).