2.4 Assess Your Understanding
Concepts and Vocabulary
Question
True or False The derivative of a product is the product of the derivatives.
Question
If \(F( x) =f(x) g(x)\), then \(F' ( x)\) =______.
Question
True or False \(\dfrac{d}{dx}x^{n}=nx^{n+1}\), for any integer \(n\).
Question
If \(f\) and \(g\neq 0\) are two differentiable functions, then \(\dfrac{d}{dx}\!\left(\dfrac{f(x)}{g(x)}\right)\) = ______.
Question
True or False \(f( x) =\dfrac{e^{x}}{x^{2}}\) can be differentiated using the Quotient Rule or by writing \(f(x) =\dfrac{e^{x}}{x^{2}}=x^{-2}e^{x}\) and using the Product Rule.
Question
If \(g\neq 0\) is a differentiable function, then \(\dfrac{d}{dx} \left[\dfrac{1}{g(x) }\right]\) = ______.
Question
If \(f(x) =x\), then \(f'' ( x)\) =______.
Question
When an object in rectilinear motion is modeled by the function \(s=s(t)\), then the acceleration \(a\) of the object at time \(t\) is given by \(a=a(t)\)= ______.
Skill Building
In Problems 9-40, find the derivative of each function.
Question
\(f( x) =xe^{x}\)
Question
\(f( x) =x^{2}e^{x}\)
Question
\(f(x)=x^{2}(x^{3}-1)\)
Question
\(f(x)=x^{4}(x+5)\)
Question
\(f(x)=(3x^{2}-5)(2x+1)\)
Question
\(f(x)=(3x-2)(4x+5)\)
Question
\(s(t)=(2t^{5}-t)(t^{3}-2t+1)\)
Question
\(F(u)=(u^{4}-3u^{2}+1)(u^{2}-u+2)\)
Question
\(f( x) =( x^{3}+1) ( e^{x}+1)\)
Question
\(f( x) =( x^{2}+1) (e^{x}+x)\)
Question
\(g(s)={\dfrac{2s}{s+1}}\)
Question
\(F(z)={\dfrac{z+1}{2z}}\)
Question
\(G(u)={\dfrac{1-2u}{1+2u}}\)
Question
\(f(w)={\dfrac{1-w^{2}}{1+w^{2}}}\)
Question
\(f(x)={\dfrac{4x^{2}-2}{3x+4}}\)
Question
\(f(x)={\dfrac{-3x^{3}-1}{2x^{2}+1}}\)
Question
\(f( w) =\dfrac{1}{w^{3}-1}\)
Question
\(g( v) =\dfrac{1}{v^{2}+5v-1}\)
Question
\(s(t)=t^{-3}\)
Question
\(G(u)=u^{-4}\)
Question
\(f(x) =-\dfrac{4}{e^{x}}\)
Question
\(f( x) =\dfrac{3}{4e^{x}}\)
Question
\(f(x)={\dfrac{10}{x^{4}}+\dfrac{3}{x^{2}}}\)
Question
\(f(x)={\dfrac{2}{x^{5}}-\dfrac{3}{x^{3}}}\)
Question
\(f(x)=3x^{3}-{\dfrac{1}{3x^{2}}}\)
Question
\(f(x)=x^{5}-{\dfrac{5}{x^{5}}}\)
Question
\(s(t)={\dfrac{1}{t}-\dfrac{1}{t^{2}}+\dfrac{1}{t^{3}}}\)
Question
\(s(t)={\dfrac{1}{t+2}+\dfrac{1}{t^{2}}+\dfrac{1}{t^{3}}}\)
Question
\(f( x) =\dfrac{e^{x}}{x^{2}}\)
Question
\(f( x) =\dfrac{x^{2}}{e^{x}}\)
Question
\(f( x) =\dfrac{x^{2}+1}{xe^{x}}\)
Question
\(f( x) =\dfrac{xe^{x}}{x^{2}-x}\)
In Problems 41-54, find \(f^\prime\) and \(f''\) for each function.
Question
\(f(x)=3x^{2}+x-2\)
Question
\(f(x)=-5x^{2}-3x\)
Question
\(f( x)=e^{x}-3\)
Question
\(f( x) =x-e^{x}\)
Question
\(f( x) =(x+5)e^{x}\)
Question
\(f( x) =3x^{4}e^{x}\)
Question
\(f( x) =(2x+1)(x^{3}+5)\)
Question
\(f( x) =(3x-5)(x^{2}-2)\)
Question
\(f(x)=x+\dfrac{1}{x}\)
Question
\(f(x)=x-\dfrac{1}{x}\)
Question
\(f(t)=\dfrac{t^{2}-1}{t}\)
Question
\(f(u)=\dfrac{u+1}{u}\)
Question
\(f( x) =\dfrac{e^{x}+x}{x}\)
Question
\(f( x) =\dfrac{e^{x}}{x}\)
Question
Find \(y^\prime\) and \(y''\) for (a) \(y={\dfrac{1}{x}}\) and (b) \(y={\dfrac{2x-5}{x}}\).
Question
Find \(\dfrac{dy}{dx}\) and \(\dfrac{d^{2}y}{dx^{2}}\) for (a) \(y={\dfrac{5}{x^{2}}}\) and (b) \(y={\dfrac{2-3x}{x}}\).
Rectilinear Motion In Problems 57-60, find the velocity \(v\) and acceleration \(a\) of an object in rectilinear motion whose distance \(s\) from the origin at time \(t\) is modeled by \(s=s( t)\).
Question
\(s(t) =16t^{2}+20t\)
Question
\(s( t) =16t^{2}+10t+1\)
Question
\(s( t) =4.9t^{2}+4t+4\)
Question
\(s(t) =4.9t^{2}+5t\)
182
In Problems 61-68, find the indicated derivative.
Question
\(f^{(4)}(x)\) if \(f(x)=x^{3}-3x^{2}+2x-5 \)
Question
\(f^{(5)}(x)\) if \(f(x)=4x^{3}+x^{2}-1\)
Question
\({\dfrac{d^{8}}{dt^{8}}\!\left(\dfrac{1}{8}t^{8}-\dfrac{1}{7} t^{7}+t^{5}-t^{3}\right) }\)
Question
\({\dfrac{d^{6}}{dt^{6}}(t^{6}+5t^{5}-2t+4)}\)
Question
\(\dfrac{d^{7}}{du^{7}}( e^{u}+u^{2})\)
Question
\(\dfrac{d^{10}}{du^{10}}( 2e^{u})\)
Question
\(\dfrac{d^{5}}{dx^{5}}( -e^{x})\)
Question
\(\dfrac{d^{8}}{dx^{8}}( 12x-e^{x})\)
In Problems 69-72:
- Find the slope of the tangent line for each function f at the given point.
- Find an equation of the tangent line to the graph of each function f at the given point.
- Find the points, if any, where the graph of the function has a horizontal tangent line.
 Graph each function, the tangent line found in (b), and any tangent lines found in (c) on the same set of axes.
Graph each function, the tangent line found in (b), and any tangent lines found in (c) on the same set of axes.
Question
\(f(x)={\dfrac{x^{2}}{x-1}}\) at \({\left(\! -1,-\dfrac{1}{2} \right)\! }\)
Question
\(f(x)={\dfrac{x}{x+1}}\) at \({( 0,0) }\)
Question
\(f(x)={\dfrac{x^{3}}{x+1}}\) at \({\left( 1,\dfrac{1}{2}\right) }\)
Question
\(f(x)={\dfrac{x^{2}+1}{x}}\) at \({\left( 2,\dfrac{5}{2}\right)\! }\)
In Problems 73-80:
- Find the points, if any, at which the graph of each function f has a horizontal tangent line.
- Find an equation for each horizontal tangent line.
- Solve the inequality \(f^\prime (x) > 0.\)
- Solve the inequality \(f^\prime (x) < 0.\)
 Graph \(f\) and any horizontal lines found in (b) on the same set of axes.
Graph \(f\) and any horizontal lines found in (b) on the same set of axes.
- Describe the graph of \(f\) for the results obtained in (c) and (d).
Question
\(f( x) =( x+1) ( x^{2}-x-11)\)
Question
\(f( x) =( 3x^{2}-2) ( 2x+1)\)
Question
\(f(x)={\dfrac{x^{2}}{x+1}}\)
Question
\(f(x)={\dfrac{x^{2}+1}{x}}\)
Question
\(f( x) =xe^{x}\)
Question
\(f( x) =x^{2}e^{x}\)
Question
\(f( x) =\dfrac{x^{2}-3}{e^{x}}\)
Question
\(f( x) =\dfrac{e^{x}}{x^{2}+1}\)
In Problems 81 and 82, use the graphs to determine each derivative.
Question
Let \(u( x) =f( x) \cdot g( x)\) and \(v( x) =\dfrac{g( x) }{f( x)}\).
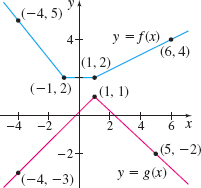
| (a) \(u' ( 0)\) | (b) \(u' ( 4)\) |
| (c) \(v' ( -2)\) | (d) \(v' ( 6)\) |
| (e) \(\dfrac{d}{dx}\left( \dfrac{1}{f( x) }\right)\)at \(x=-2\) | (f) \(\dfrac{d}{dx}\left( \dfrac{1}{g( x) }\right)\) at \(x=4\) |
Question
Let \(F( t) =f( t) \cdot g( t)\) and \(G( t) =\dfrac{g( t) }{f( t) }\).
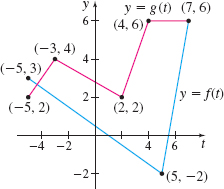
| (a) \(F^\prime ( 0)\) | (b) \(F^\prime ( 3)\) |
| (c) \(F^\prime ( -4)\) | (d) \(G^\prime ( -2)\) |
| (e) \(G^\prime ( -1)\) | (f) \(\dfrac{d}{dt}\left( \dfrac{1}{f( t) }\right)\) at \(t=3\) |
Applications and Extensions
Question
Movement of an Object An object is propelled vertically upward from the ground with an initial velocity of \(39.2{\text{m/s}}\). The distance \(s\) (in meters) of the object from the ground after \( t\) seconds is \(s= s(t)= -4.9t^{2}+39.2t\).
- What is the velocity of the object at time \(t\)?
- When will the object reach its maximum height?
- What is the maximum height?
- What is the acceleration of the object at any time \(t\)?
- How long is the object in the air?
- What is the velocity of the object upon impact with the ground?
- What is the total distance traveled by the object?
Question
Movement of a Ball A ball is thrown vertically upward from a height of \(6{\text{ft}}\) with an initial velocity of \(80\text{ft/s}\). The distance \(s\) (in feet) of the ball from the ground after \(t\) seconds is \(s= s(t)=6+80t-16t^{2}\).
- What is the velocity of the ball after 2 seconds?
- When will the ball reach its maximum height?
- What is the maximum height the ball reaches?
- What is the acceleration of the ball at any time \(t\)?
- How long is the ball in the air?
- What is the velocity of the ball upon impact with the ground?
- What is the total distance traveled by the ball?
Question
Environmental Cost The cost \(C\), in thousands of dollars, for the removal of a pollutant from a certain lake is given by the function \(C( x) =\dfrac{5x}{110-x},\) where \(x\) is the percent of pollutant removed.
183
- What is the domain of \(C?\)
 Graph \(C.\)
Graph \(C.\)- What is the cost to remove 80% of the pollutant?
- Find \(C’ ( x) ,\) the rate of change of the cost \(C\) with respect to the amount of pollutant removed.
- Find the rate of change of the cost for removing 40%, 60%, 80%, and 90% of the pollutant.
- Interpret the answers found in (e).
Question
Investing in Fine Art The value \(V\) of a painting \(t\) years after it is purchased is modeled by the function \[ \begin{eqnarray*} V( t) =\dfrac{100t^{2}+50}{t}+400, 1 ≤ t ≤ 5\\[-19pt] \end{eqnarray*} \]
- Find the rate of change in the value \(V\) with respect to time.
- What is the rate of change in value after 1 year?
- What is the rate of change in value after 3 years?
- Interpret the answers in (b) and (c).
Question
Drug Concentration The concentration of a drug in a patient’s blood \(t\) hours after injection is given the function \(f( t) =\dfrac{0.4t}{2t^{2}+1}\) (in milligrams per liter).
- Find the rate of change of the concentration with respect to time.
- What is the rate of change of the concentration after 10 min? After 30 min? After 1 hour?
- Interpret the answers found in (b).
 Graph \(f\) for the first 5 hours after administering the drug.
Graph \(f\) for the first 5 hours after administering the drug.- From the graph, approximate the time (in minutes) at which the concentration of the drug is highest. What is the highest concentration of the drug in the patient’s blood?
Question
Population Growth A population of 1000 bacteria is introduced into a culture and grows in number according to the formula \(P( t) =1000\left( 1+\dfrac{4t}{100+t^{2}}\right)\), where \(t\) is measured in hours.
- Find the rate of change in population with respect to time.
- What is the rate of change in population at \(t=1\), \(t=2\), \(t=3\), and \(t=4\)?
- Interpret the answers found in (b).
 Graph \(P=P(t)\), \(0 ≤ t ≤ 20\).
Graph \(P=P(t)\), \(0 ≤ t ≤ 20\).- From the graph, approximate the time (in hours) when the population is the greatest. What is the maximum population of the bacteria in the culture?
Question
Economics The price-demand function for a popular e-book is given by \(D( p) =\dfrac{100,000}{p^{2}+10p+50},\) \(5 ≤ p ≤ 20,\) where \(D = D(p)\) is the quantity demanded at the price \(p\) dollars.
- Find \(D’ ( p) \), the rate of change of demand with respect to price.
- Find \(D’ ( 5)\), \(D’ ( 10)\), and \(D’ ( 15)\).
- Interpret the results found in (b).
Question
Intensity of Light The intensity of illumination \(I\) on a surface is inversely proportional to the square of the distance \(r\) from the surface to the source of light. If the intensity is 1000 units when the distance is 1 meter from the light, find the rate of change of the intensity with respect to the distance when the source is 10 meters from the surface.
Question
Ideal Gas Law The Ideal Gas Law, used in chemistry and thermodynamics, relates the pressure \(p\), the volume \(V\), and the absolute temperature \(T\) (in Kelvin) of a gas, using the equation \(pV=nRT\), where \(n\) is the amount of gas (in moles) and \(R=8.31\) is the ideal gas constant. In an experiment, a spherical gas container of radius \(r\) meters is placed in a pressure chamber and is slowly compressed while keeping its temperature at 273 K.
- Find the rate of change of the pressure \(p\) with respect to the radius \( r\) of the chamber. (Hint: The volume \(V\) of a sphere is \(V=\dfrac{4}{3 }\pi r^{3}.\))
- Interpret the sign of the answer found in (a).
- If the sphere contains 1.0 mol of gas, find the rate of change of the pressure when \(r=\dfrac{1}{4}m\). (Note: The metric unit of pressure is the pascal, \(Pa\)).
Question
Body Density The density \(\rho\) of an object is its mass \(m\) divided by its volume \(V\); that is, \(\rho =\dfrac{m}{V}\). If a person dives below the surface of the ocean, the water pressure on the diver will steadily increase, compressing the diver and therefore increasing body density. Suppose the diver is modeled as a sphere of radius \(r\).
- Find the rate of change of the diver’s body density with respect to the radius \(r\) of the sphere. (Hint: The volume \(V\) of a sphere is \(V= \dfrac{4}{3}\pi r^{3}.\))
- Interpret the sign of the answer found in (a).
- Find the rate of change of the diver’s body density when the radius is 45\({cm}\) and the mass is \(80{,}000{g}\) (\(80{kg}\)).
Jerk and Snap Problems 93-96 use the following discussion:
Suppose that an object is moving in rectilinear motion so that its distance \( s\) from the origin at time \(t\) is given by the function \(s=s( t) \). The velocity \(v=v( t)\) of the object at time \(t\) is the rate of change of the distance \(s\) with respect to time, namely, \(v=v( t) =\dfrac{ds}{dt}.\) The acceleration \(a=a( t)\) of the object at time \(t\) is the rate of change of the velocity with respect to time, namely, \[ a=a( t) =\dfrac{dv}{dt}= \dfrac{d}{dt}\!\left( \dfrac{ds}{dt}\right) =\dfrac{d^{2}s}{dt^{2}}. \]
There are also physical interpretations to the third derivative and the fourth derivative of \( s=s( t) .\) The jerk \(J=J( t)\) of the object at time \(t\) is the rate of change in the acceleration \(a\) with respect to time; that is, \[ J=J( t) = \dfrac{da}{dt}= \dfrac{d}{ dt}\!\left( \dfrac{dv}{dt}\right) =\dfrac{d^{2}v}{dt^{2}}=\dfrac{d^{3}s}{dt^{3}} \]
184
The snap \(S= S(t)\) of the object at time \(t\) is the rate of change in the jerk \(J\) with respect to time; that is, \[ S=S(t) =\dfrac{dJ}{dt}= \dfrac{d^{2}a}{dt^{2}}=\dfrac{d^{3}v}{dt^{3}}=\dfrac{d^{ 4 }s}{dt^{ 4 }}. \]
Engineers take jerk into consideration when designing elevators, aircraft, and cars. In these cases, they try to minimize jerk, making for a smooth ride. But when designing thrill rides, such as roller coasters, the jerk is increased, making for an exciting experience.
Question
Rectilinear Motion As an object in rectilinear motion moves, its distance \(s\) from the origin at time \(t\) is given by \(s = s(t) =t^{3}-t+1\), where \(s\) is in meters and \(t\) is in seconds.
- Find the velocity \(v\), acceleration \(a\), jerk \(J,\) and snap \(S\) of the object at time \(t.\)
- When is the velocity of the object 0 m/s?
- Find the acceleration of the object at \(t=2\) and at \(t\) = 5.
- Does the jerk of the object ever equal 0 m/s\(^{3}\)?
- How would you interpret the snap for this object in rectilinear motion?
Question
Rectilinear Motion As an object in rectilinear motion moves, its distance \(s\) from the origin at time \(t\) is given by \(s=s(t) =\dfrac{1}{6}t^{4}-t^{2}+\dfrac{1}{2}t\)+4, where \(s\) is in meters and \(t\) is in seconds.
- Find the velocity \(v\), acceleration \(a\), jerk \(J\), and snap \(S\) of the object at any time \(t.\)
- Find the velocity of the object at \(t=0\) and at \(t=3\).
- Find the acceleration of the object at \(t=0\). Interpret your answer.
- Is the jerk of the object constant? In your own words, explain what the jerk says about the acceleration of the object.
- How would you interpret the snap for this object in rectilinear motion?
Question
Elevator Ride Quality The ride quality of an elevator depends on several factors, two of which are acceleration and jerk. In a study of 367 persons riding in a 1600-kg elevator that moves at an average speed of 4 m/s, the majority of riders were comfortable in an elevator with vertical motion given by \[ s(t) =4t+0.8t^{2}+0.333t^{3} \]
- Find the acceleration that the riders found acceptable.
- Find the jerk that the riders found acceptable.
Source: Elevator Ride Quality, January 2007, http://www.lift-report.de/index.php/news/176/368/Elevator-Ride-Quality.
Question
Elevator Ride Quality In a hospital, the effects of high acceleration or jerk may be harmful to patients, so the acceleration and jerk need to be lower than in standard elevators. It has been determined that a 1600-kg elevator that is installed in a hospital and that moves at an average speed of 4 m/s, should have vertical motion \[ s(t) =4t+0.55t^{2}+0.1167t^{3} \]
- Find the acceleration of a hospital elevator.
- Find the jerk of a hospital elevator.
Source: Elevator Ride Quality, January 2007, http://www.lift-report.de/index.php/news/176/368/Elevator-Ride-Quality.
Question
Current Density in a Wire The current density \(J\) in a wire is a measure of how much an electrical current is compressed as it flows through a wire and is modeled by the function \(J(A) =\dfrac{I}{A}\), where \(I\) is the current (in amperes) and \(A\) is the cross-sectional area of the wire. In practice, current density, rather than merely current, is often important. For example, superconductors lose their superconductivity if the current density is too high.
- As current flows through a wire, it heats the wire, causing it to expand in area \(A\). If a constant current is maintained in a cylindrical wire, find the rate of change of the current density \(J\) with respect to the radius \(r\) of the wire.
- Interpret the sign of the answer found in (a).
- Find the rate of change of current density with respect to the radius \(r\) when a current of 2.5 amps flows through a wire of radius \( r=0.50\) millimeter.
Question
Derivative of a Reciprocal, Function Prove that if a function \(g\) is differentiable, then \(\dfrac{d}{dx}\!\left[\dfrac{1}{g(x)}\right]\) = − \(\dfrac{g^\prime (x)}{[g(x)]^{2}}\), provided \(g(x)\neq 0\).
Question
Extended Product Rule Show that if \(f,g\), and \(h\) are differentiable functions, then \[ \begin{eqnarray*} \frac{d}{dx}[f(x)g(x)h(x)]&=&f(x)g(x){h}^{\prime }(x)+f(x){g}^{\prime }(x)h(x)\\ &&+{f}^{\prime }(x)g(x)h(x) \end{eqnarray*} \]
From this, deduce that \[ \frac{d}{dx}[f(x)]^{3}=3[f(x)]^{2}f^\prime (x) \]
In Problems 100–105, use the Extended Product Rule (Problem 99) to find \(y^\prime\).
Question
\(y=(x^{2}+1)(x-1)(x+5)\)
Question
\(y=(x-1)(x^{2}+5)(x^{3}-1)\)
Question
\(y=(x^{4}+1)^{3}\)
Question
\(y=(x^{3}+1)^{3}\)
Question
\(y=(3x+1){\left(1+\dfrac{1}{x}\right) (x^{-5}+1)}\)
Question
\(y={\left(1-\dfrac{1}{x}\right)\!\! \left(1-\dfrac{1}{x^{2}}\right)\!\! \left(1-\dfrac{1}{x^{3}}\right) }\)
Question
(Further) Extended Product Rule Write a formula for the derivative of the product of four differentiable functions. That is, find a formula for \(\dfrac{d}{dx}[ f_{1}(x) f_{2}(x) f_{3}(x) f_{4}(x)]\). Also find a formula for \(\dfrac{d}{dx}[f(x)]^{4}.\)
185
Question
If \(f\) and \(g\) are differentiable functions, show that if \(F(x)\)=\(\dfrac{1}{f(x) g(x)}\), then \[ F’ (x)=-F(x)\left[ {\frac{f^\prime (x)}{f(x)}}+{\frac{g^\prime (x)}{g(x)}}\right] \] provided \(f(x) \neq 0,\) \(g(x) \neq 0.\)
Question
Higher-Order Derivatives If \(f(x)=\dfrac{1}{1-x}\), find a formula for the \(n\)th derivative of \(f\). That is, find \(f^{(n)}(x)\).
Question
Let \(f(x)=\dfrac{x^{6}-x^{4}+x^{2}}{x^{4}+1}\). Rewrite \(f\) in the form \((x^{4}+1) f(x) = x^{6}-x^{4}+x^{2}\). Now find \(f^\prime (x)\) without using the quotient rule.
Question
If \(f\) and \(g\) are differentiable functions with \(f\neq -g\), find the derivative of \(\dfrac{fg}{f+g}\).
Question
![]() \(f(x) =\dfrac{2x}{x+1}\).
\(f(x) =\dfrac{2x}{x+1}\).
- Use technology to find \(f^\prime (x).\)
- Simplify \(f^\prime\) to a single fraction using either algebra or a CAS.
- Use technology to find \(f^{(5)}(x)\). (Hint: Your CAS may have a method for finding higher-order derivatives without finding other derivatives first.)
Challenge Problems
Question
Suppose \(f\) and \(g\) have derivatives up to the fourth order. Find the first four derivatives of the product \(fg\) and simplify the answers. In particular, show that the fourth derivative is \[ \dfrac{d^4}{dx^4} (fg) = f^{(4)}g+4f^{(3)}g^{(1)}+6f^{(2)}g^{(2)}+4f^{(1)}g^{(3)}+fg^{(4)} \]
Identify a pattern for the higher-order derivatives of \(fg\).
Question
Suppose \(f_{1}(x),\ldots ,f_{n}(x)\) are differentiable functions.
- Find \(\dfrac{d}{dx}[ f_{1}(x)\cdot \cdots \cdot f_{n}(x)].\)
- Find \(\dfrac{d}{dx}\!\!\left[ {\dfrac{1}{f_{1}(x)\cdot \cdots \cdot f_{n}(x)}}\right]\! .\)
Question
Let \(a,b,c\), and \(d\) be real numbers. Define \[ \begin{equation*} \left\vert \begin{array}{l@{\quad}l} {a} & {b} \\ {c} & {d} \end{array} \right\vert =ad-bc \end{equation*} \]
This is called a \(2\times 2\) determinant and it arises in the study of linear equations. Let \(f_{1}(x),f_{2}(x),f_{3}(x)\), and \(f_{4}(x)\) be differentiable and let \[ D(x)=\left\vert \begin{array}{l@{\quad}l} {f_{1}(x)} & {f_{2}(x)} \\[3pt] {f_{3}(x)} & {f_{4}(x)} \end{array} \right\vert \]
Show that \[ D^{\prime }(x)=\left\vert \begin{array}{l@{\quad}l} {f_{1}' (x)} & {f_{2}' (x)} \\[3pt] {f_{3}(x)} & {f_{4}(x)} \end{array} \right\vert +\left\vert \begin{array}{l@{\quad}l} {f_{1}(x)} & {f_{2}(x)} \\[3pt] {f_{3}' (x)} & {f_{4}' (x)} \end{array} \right\vert \]
Question
Let \(f_{0}(x) =x-1\)
\[ f_{1}( x) =1+\dfrac{1}{x-1}\]
\[f_{2}( x) =1+\dfrac{1}{1+\dfrac{1}{x-1}}\]
\[f_{3}( x) =1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{x-1}}} \]
- Write \(f_{1}\), \(f_{2}\,\) \(f_{3}\), \(f_{4}\) and \(f_{5}\) in the form \(\dfrac{ax+b}{cx+d}\).
- Using the results from (a), write the sequence of numbers representing the coefficients of \( x\) in the numerator, beginning with \(f_{0}(x) =x-1\).
- Write the sequence in (b) as a recursive sequence. (Hint: Look at the sums of consecutive terms.)
- Find \(f_{0}'\), \(f_{1}'\), \(f_{2}'\), \(f_{3}'\), \(f_{4}'\), and \(f_{5}'\).
