3.5 Assess Your UnderstandingPrinted Page 241
Concepts and Vocabulary
True or False If \(f\) is a function with both first and second derivatives defined on an interval containing \(x_{0}\), then \(f\) can be approximated by the Taylor Polynomial \(P_{2}( x) =f( x_{0}) +f^\prime ( x_{0}) ( x-x_{0}) +f^{\prime \prime} ( x_{0}) ( x-x_{0}) ^{2}.\)
False
True or False A Taylor Polynomial approximation \(P_{n}\) for a function \(f\) at \(x_{0}\) has the following properties: \(P_{n}( x_{0}) =f( x_{0}) \) and \(P_{n}^{k}( x_{0}) =f^{k}( x_{0}) \) for derivatives of all orders from \(k=1\) to \(k=n\).
True
242
Skill Building
In Problems 3–28, for each function \(f\) find the Taylor Polynomial \(P_{5}( x) \) for \(f\) at the given \(x_{0}\).
\(f(x)=3x^{3}+2x^{2}-6x+5\) at \(x_{0}=1\)
\(P_5(x)=3 (x-1)^3+11 (x-1)^2+7 (x-1)+4\)
\(f(x)=4x^{3}-2x^{2}-4\) at \(x_{0}=1\)
\(f(x)=2x^{4}-6x^{3}+x\) at \(x_{0}=-1\)
\(P_5(x)=2 (x+1)^4-14 (x+1)^3+30 (x+1)^2-25 (x+1)+7\)
\(f(x)=-3x^{4}+2x^{2}-5\) at \(x_{0}=-1\)
\(f(x)=x^{5}\) at \(x_{0}=2\)
\(P_5(x)=(x - 2)^5 + 10 (x-2)^4+40 (x-2)^3+80 (x-2)^2+80 (x-2)+32\)
\(f(x)=x^{6}\) at \(x_{0}=3\)
\(f(x)=\ln x\) at \(x_{0}=1\)
\(P_5(x)=\dfrac{1}{5} (x-1)^5-\dfrac{1}{4} (x-1)^4+\dfrac{1}{3} (x-1)^3-\dfrac{1}{2} (x-1)^2+(x-1)\)
\(f(x)=\ln (1+x)\) at \(x_{0}=0\)
\(f(x)=\dfrac{1}{x}\) at \(x_{0}=1\)
\(P_5(x)=-(x-1)^5+(x-1)^4-(x-1)^3+(x-1)^2 -(x - 1)+1 \)
\(f(x)=\dfrac{1}{x^{2}}\) at \(x_{0}=1\)
\(f(x)=\cos x\) at \(x_{0}=0\)
\(P_5(x)= \dfrac{x^4}{24}-\dfrac{x^2}{2}+1\)
\(f(x)=\sin x\) at \(x_{0}=\dfrac{\pi }{4}\)
\(f( x) =e^{2x}\) at \(x_{0}=0\)
\(P_5(x)= \dfrac{4x^5}{15} + \dfrac{2 x^4}{3}+\dfrac{4 x^3}{3}+2 x^2+2 x+1\)
\(f(x)=e^{-x}\) at \(x_{0}=0\)
\(f(x)=\dfrac{1}{1-x}\) at \(x_{0}=0\)
\(P_5(x)=x^5 + x^4+x^3+x^2+x+1\)
\(f(x)=\dfrac{1}{1+x}\) at \(x_{0}=0\)
\(f(x)=\dfrac{1}{(1+x)^{2}}\) at \(x_{0}=0\)
\(P_5(x)=-6x^5 + 5x^4 -4 x^3+3 x^2-2 x+1\)
\(f(x)=\dfrac{1}{1+x^{2}}\) at \(x_{0}=0\)
\(f(x)=x\ln x\) at \(x_{0}=1\)
\(P_5(x)=- \dfrac{1}{20} (x - 1)^5 + \dfrac{1}{12} (x-1)^4-\dfrac{1}{6} (x-1)^3+\dfrac{1}{2} (x-1)^2+(x-1)\)
\(f(x)=xe^{x}\) at \(x_{0}=1\)
\(f(x)=\sqrt{3+x^{2}}\) at \(x_{0}=1\)
\(P_5(x)=\dfrac{15}{4096} (x - 1)^5 + \dfrac{3}{1024} (x - 1)^4 -\dfrac{3}{64} (x-1)^3+\dfrac{3}{16} (x-1)^2+\dfrac{1}{2}(x-1)+2\)
\(f(x)=\sqrt{1+x}\) at \(x_{0}=0\)
\(f(x)=\tan x\) at \(x_{0}=\dfrac{\pi }{4}\)
\(P_5(x)=\dfrac{64}{15} \left(x - \dfrac{\pi}{4}\right)^5 + \dfrac{10}{3} \left(x-\dfrac{\pi }{4}\right)^4+\dfrac{8}{3} \left(x-\dfrac{\pi }{4}\right)^3+2 \left(x-\dfrac{\pi }{4}\right)^2 + 2 \left(x-\dfrac{\pi }{4}\right)+1\)
\(f(x)=\sec x\) at \(x_{0}=0\)
\(f(x)=\tan ^{-1}x\) at \(x_{0}=0\)
\(P_5(x)= \dfrac{x^5}{5} - \dfrac{x^3}{3} + x \)
\(f(x)=\sin ^{-1}x\) at \(x_{0}=0\)
Applications and Extensions
In Problems 29–32, express each polynomial as a polynomial in \((x-1)\) by writing the Taylor Polynomial for \(f\) at \(1\).
\(f(x)=3x^{2}-6x+4\)
\(f(x)=3 (x-1)^2+1\)
\(f(x)=4x^{2}-x+1\)
\(f(x)=x^{3}+x^{2}-8\)
\(f(x)=(x-1)^3+4 (x-1)^2+5 (x-1)-6\)
\(f(x)=x^{4}+1\)
In Problems 33 – 40:
- (a) find the indicated Taylor polynomial for each function \(f\) at \(x_{0}\).
- (b)
 Graph \(f\) and the Taylor polynomial found in (a).
Graph \(f\) and the Taylor polynomial found in (a).
\(f( x) =\sin ^{-1}x\) at \(x_{0}=\dfrac{1}{2}\), \(P_{4}(x)\)
- (a) \(P_4(x)=\dfrac{28 \left(x-\dfrac{1}{2}\right)^4}{27 \sqrt{3}}+\dfrac{8 \left(x-\dfrac{1}{2}\right)^3}{9 \sqrt{3}}+\dfrac{2 \left(x-\dfrac{1}{2}\right)^2}{3 \sqrt{3}}+\dfrac{2 \left(x-\dfrac{1}{2}\right)}{\sqrt{3}}+\dfrac{\pi }{6}\)
- (b)
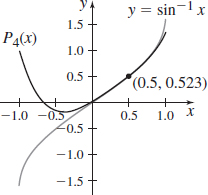
\(f(x)=\tan ^{-1}x\) at \(x_{0}=1\), \(P_{5}(x)\)
\(f( x) =\dfrac{x}{\sqrt{x^{2}+3}}\) at \(x_{0}=1\), \(P_{5}(x)\)
- (a) \(P_5(x)={-171\over 16384}(x-1)^5+{75\over 4096}(x-1)^4+{3\over 256}(x-1)^3-{9\over 64}(x-1)^2+ {3\over 8}(x-1)+{1\over 2}\)
- (b)
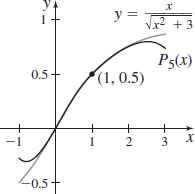
\(f( x) =x\sqrt[3]{x^{2}+5}\) at \(x_{0}=2\), \(P_{5}(x)\)
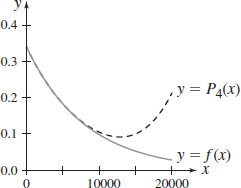
Uninhibited Decay \(f( x) =0.34e^{[(-\ln 2)/5600] x}\) at \(x=0\), \(P_{4}(x)\)
- (a) P4(x)
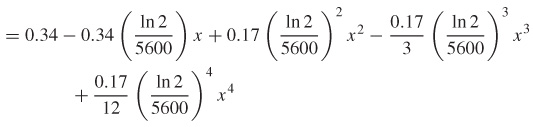
- (b)
Uninhibited Growth \(f( x) =5000e^{0.04x}\) at \(x=0\), \(P_{4}(x)\)
Logistic Population Growth Model \(f( x) =\dfrac{100}{1+30.2e^{-0.2x}}\) at \(x_{0}=0\), \(P_{3}(x)\)
- (a) \(P_3(x)=3. 205+0.620 x+0.05 8x^2+0.003 4 x^3\)
- (b)
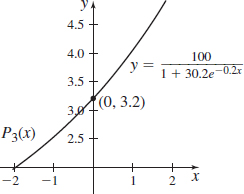
Gompertz Population Growth Model \(f(x)=100e^{-3e^{-0.2x}}\) at \(x_{0}=0\), \(P_{3}(x)\)
The Taylor Polynomial \(P_{7}( x)\) for \(f( x) =\sin x\) at \(0\) has only terms with odd powers. See Example 2.
- (a) Discuss why this is true. Does this property hold for the Taylor Polynomial \(P_{n}( x)\) for any number \(n\)?
- (b) Investigate the Taylor Polynomial \(P_{7}( x) \) for \(f\) at \(\frac{\pi}{2}\). Does this Taylor Polynomial have only odd terms? Explain why or why not.
See Student Solutions Manual.
The Taylor Polynomial \(P_{6}( x) \) for \(f( x) =\cos x\) at \(0\) has only terms with even powers. See Problem 13.
- (a) Discuss why this is true. Does this property hold for the Taylor Polynomial \(P_{n}( x) \) for any \(n?\)
- (b) Investigate the Taylor Polynomial \(P_{6}( x) \) for \(f\) at \(\frac{\pi}{2}\). Does this Taylor Polynomial have only even terms? Explain why or why not.
Challenge Problems
The graphs of \(y=\sin x\) and \(y=\lambda x\) intersect near \(x=\pi \) if \(\lambda \) is small. Let \(f(x)=\sin x-\lambda x\). Find the Taylor Polynomial \(P_{2}( x)\) for \(f\) at \(\pi\), and use it to show that an approximate solution of the equation \(\sin x=\lambda x\) is \(x=\dfrac{\pi }{1+\lambda}\).
\(P_{2}(x)=-\lambda \pi - (1+\lambda)(x-\pi)\) See Student Solutions Manual.
The graphs of \(y=\cot x\) and \(y=\lambda x\) intersect near \(x=\frac{\pi}{2} \) if \(\lambda \) is small. Let \(f(x)=\cot x-\lambda x\). Find the Taylor Polynomial \(P_{2}( x)\) for \(f\) at \(\dfrac{\pi }{2},\) and use it to find an approximate solution of the equation \(\cot x=\lambda x\).
