3.6 Assess Your Understanding

Printed Page 249

249

Concepts and Vocabulary

  1. True or False \({\mathop{\rm{csch}}}x=\dfrac{1}{\cosh x}\).

False

  1. In terms of \(\sinh x\) and \(\cosh x,\) \(\tanh x=\) _________________.

\(\sinh x{/}\cosh x\)

  1. True or False The domain of \(y=\cosh x\) is \([1,\infty)\).

False

  1. Multiple Choice The function \(y=\cosh x\) is [(a) even, (b) odd, (c) neither].

(a)

  1. True or False \(\cosh ^{2}x+\sinh ^{2}x=1\).

False

  1. True or False \(\dfrac{d}{dx}\sinh x=\dfrac{1}{\ \sqrt{x^{2}+1}}\).

False

  1. True or False The function \(y=\sinh ^{-1}x\) is defined for all real numbers \(x\).

True

  1. True or False \(\dfrac{d}{dx}\sinh^{-1}x=\cosh ^{-1}x\)

False

Skill Building

In Problems 9–14, find the exact value of each expression.

  1. \({\mathop{\rm{csch}}}(\ln 3) \)

\({3\over 4}\)

  1. \({\mathop{\rm{sech}}}( \ln 2) \)

  1. \(\cosh ^{2}(5) -\sinh ^{2}(5) \)

\(1\)

  1. \(\cosh ( -\!\ln 2) \)

  1. \(\tanh 0\)

\(0\)

  1. \(\sinh \left(\ln \dfrac{1}{2}\right) \)

In Problems 15–24, establish each identity.

  1. \(\tanh ^{2}x+{\mathop{\rm{sech}}}^{2}x=1\)

See Student Solutions Manual.

  1. \(\coth ^{2}x-{\mathop{\rm{csch}}}^{2}x=1\)

  1. \(\sinh (-A)=-\sinh A\)

See Student Solutions Manual.

  1. \(\cosh (-A)=\cosh A\)

  1. \(\sinh (A+B)=\sinh A\cosh B+\cosh A\sinh B\)

See Student Solutions Manual.

  1. \(\cosh (A+B)=\cosh A\cosh B+\sinh A\sinh B\)

  1. \(\sinh (2x) =2 \sinh x \cosh x\)

See Student Solutions Manual.

  1. \(\cosh (2x) =\cosh ^{2}x+\sinh ^{2}x\)

  1. \(\cosh (3x) =4\cosh ^{3}x-3\cosh x\)

See Student Solutions Manual.

  1. \(\tanh (2x) = \dfrac{2\tanh x}{1+\tanh ^{2}x}\)

In Problems 25–48, find \(y^\prime \).

  1. \(y=\sinh (3x) \)

\(y'=3 \cosh (3 x)\)

  1. \(y=\cosh \dfrac{x}{2}\)

  1. \(y=\cosh (x^{2}+1)\)

\(y'=2\, x \sinh (x^2+1)\)

  1. \(y=\cosh (2x^{3}-1)\)

  1. \(y=\coth \dfrac{1}{x}\)

\(y'=\dfrac{\hbox{csch}^2\left(\dfrac{1}{x}\right)}{x^2}\)

  1. \(y=\tanh ( x^{2})\)

  1. \(y=\sinh x \cosh (4x) \)

\(y'=4 \,\sinh x\, \sinh (4 x)+\,\cosh x\, \cosh (4 x)\)

  1. \(y=\sinh (2x) \cosh (-x)\)

  1. \(y=\cosh ^{2}x\)

\(y'=2\, \cosh x \, \sinh x\)

  1. \(y=\tanh ^{2}x\)

  1. \(y=e^{x}\cosh x\)

\(y'=e^x\, \sinh x + e^x \,\cosh x\)

  1. \(y=e^{x}(\cosh x+\sinh x)\)

  1. \(y=x^{2}\;{\mathop{\rm{sech}}}\;x\)

\(y'=2 x\,\hbox{sech}\;x - x^2 \tanh x\; \hbox{sech}\; x\)

  1. \(y=x^{3}\tanh x\)

  1. \(y=\cosh ^{-1}( 4x)\)

\(y'=\dfrac{4}{ \sqrt{16x^2-1} }\)

  1. \(y=\sinh ^{-1}(3x)\)

  1. \(y=\tanh ^{-1}(x^{2}-1)\)

\(y'=\dfrac{2 x}{1-\left(1-x^2\right)^2}\)

  1. \(y=\cosh ^{-1}(2x+1)\)

  1. \(y=x\sinh ^{-1}x\)

\(y'=\dfrac{x}{\sqrt{x^2+1}}+\sinh ^{-1} x\)

  1. \(y=x^{2}\cosh ^{-1}x\)

  1. \(y=\tanh ^{-1}(\tan x)\)

\(y'=\dfrac{\sec ^2 x}{1-\tan ^2 x}\)

  1. \(y=\sinh ^{-1}(\sin x)\)

  1. \(y=\cosh ^{-1}\big( \ \sqrt{x^{2}-1}\big)\), \(x>\ \sqrt{2}\)

\(y'=\dfrac{x}{\sqrt{x^2-1} \sqrt{x^2-2} }\)

  1. \(y=\sinh ^{-1}\big( \ \sqrt{x^{2}+1}\big) \)

Applications and Extensions

  1. Taylor Polynomial Write the Taylor Polynomial \(P_{6}( x) \) for \(g(x)=\cosh \,x\) at \(0.\)

\(P_6(x)=\dfrac{x^6}{720}+\dfrac{x^4}{24}+\dfrac{x^2}{2}+1\)

  1. Taylor Polynomial Write the Taylor Polynomial \(P_{7}( x) \) for \(f(x)=\tanh \,x\) at \(0.\)

  1. Catenary A cable is suspended between two supports of the same height that are \(100{\,{\rm{m}}}\) apart. If the supports are placed at \(( -50,0) \) and \(( 50,0)\), the equation that models the height of the cable is \(y=12\cosh \dfrac{x}{12}+20\). Find the angle \(\theta \) at which the cable meets each support.

\(\theta \approx 0.031\) radians \(\approx 1.776^{\circ}\)

  1. Catenary A town hangs strings of holiday lights across the road between utility poles. Each set of poles is \(12{\,{\rm{m}}}\) apart. The strings hang in catenaries modeled by \(y=15\cosh \dfrac{x}{15}-10\).

    1. (a) Find the slope of the tangent line where the lights meet the pole.
    2. (b) Find the angle at which the string of lights meets the pole.

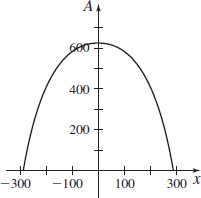
  1. Catenary The famous Gateway Arch to the West in St. Louis, Missouri, is constructed in the shape of a modified inverted catenary. (Modified because the weight is not evenly dispersed throughout the arch.) If \(y\) is the height of the arch (in feet) and \(x=0\) corresponds to the center of the arch (its highest point), an equation for the arch is given by \[ y=-68.767\cosh \left( \dfrac{0.711x}{68.767}\right) + 693.859 {\,{\rm{ft}}}, \]

    1. (a) Find the maximum height of the arch.
    2. (b) Find the width of the arch at ground level.
    3. (c) What is the slope of the arch \(50{\,{\rm{ft}}}\) from its center?
    4. (d) What is the slope of the arch \(200{\,{\rm{ft}}}\) from its center?
    5. (e) Find the angle (in degrees) that the arch makes with the ground. (Assume the ground is level.)
    6. (f) Graph the equation that models the Gateway Arch, and explain how the graph supports the answers found in (a)–(e).

  1. (a) \(625.092\) ft
  2. (b) \(580.744\) ft
  3. (c) \(\pm 0.384\)
  4. (d) \(\pm2.766\)
  5. (e) \(82.026^\circ\)
  6. (f)

  1. Establish the identity \((\cosh x+\sinh x)^{n}=\cosh (nx) +\sinh ( nx)\) for any real number \(n\).

    1. (a) Show that if \(y=\cosh^{-1}x\), then \(y^{\prime}=\dfrac{1}{\ \sqrt{x^{2}-1}}\).
    2. (b) What is the domain of \(y^\prime \)?

  1. (a) See Student Solutions Manual.
  2. (b) { x | x > 1 }
    1. (a) Show that if \(y=\tanh^{-1}x\), then \(y^{\prime}=\dfrac{1}{1-x^{2}}\).
    2. (b) What is the domain of \(y^\prime \)?

  1. Show that \(\dfrac{d}{dx}\tanh x={\mathop{\rm{sech}}}^{2}x\).

See Student Solutions Manual.

250

  1. Show that \(\dfrac{d}{dx}\coth x=-{\mathop{\rm{csch}}}^{2}x\).

  1. Show that \(\dfrac{d}{dx}{\mathop{\rm{sech}}}x=-{\mathop{\rm{sech}}}x \tanh x\)

See Student Solutions Manual.

  1. Show that \(\dfrac{d}{dx}{\mathop{\rm{csch}}}x=-{\mathop{\rm{csch}}} x \coth x\)

  1. Show that \(\tanh ^{-1}x=\dfrac{1}{2}\ln \left(\dfrac{1+x}{1-x}\right)\), \(-1<x<1\).

See Student Solutions Manual.

  1. Show that \(\cosh ^{-1}x=\ln (x+\ \sqrt{x^{2}-1})\), \(x ≥ 1\).

  1. Show that \(\coth ^{-1}x=\dfrac{1}{2}\ln \left( \dfrac{x+1}{x-1}\right)\), \(\vert x\vert >1\).

See Student Solutions Manual.

Challenge Problems

In Problems 64 and 65, find each limit.

  1. \(\lim\limits_{x\rightarrow 0}\left( \dfrac{\sinh x}{x}\right) \)

  1. \(\lim\limits_{x\rightarrow 0}\left( \dfrac{\cosh x-1}{x}\right) \)

\(0\)

    1. (a) Sketch the graph of \(y=f( x) =\dfrac{1}{2} ( e^{x}+e^{-x}) .\)
    2. (b) Let \(R\) be a point on the graph and let \(r,\) \(r≠ 0,\) be the \( x\)-coordinate of \(R.\) The tangent line to the graph of \(f\) at \(R\) crosses the \(x\)-axis at the point \(Q.\) Find the coordinates of \(Q\) in terms of \(r.\)
    3. (c) If \(P\) is the point \(( r,0) ,\) find the length of the line segment \(PQ\) as a function of \(r\) and the limiting value of this length as \(r\) increases without bound.

  1. What happens if you try to find the derivative of \(f( x) =\sin ^{-1}( \cosh x) \)? Explain why this occurs.

See Student Solutions Manual.

  1. Let \(f(x)=x\sinh ^{-1}x\).

    1. (a) Show that \(f\) is an even function.
    2. (b) Find \(f^\prime (x)\) and \(f^{\prime \prime} ( x) \).