OBJECTIVES

When you finish this section, you should be able to:

1. Solve optimization problems (p. 318)

Steps for Solving Optimization Problems

Step 1 Read the problem until you understand it and can identify the quantity for which a maximum or minimum value is to be found. Assign a symbol to represent it.

Step 2 Assign symbols to represent the other variables in the problem. If possible, draw a picture and label it. Determine relationships among the variables.

Step 3 Express the quantity to be maximized or minimized as a function of one of the variables, and determine a meaningful domain for the function.

Step 4 Find the absolute maximum value or absolute minimum value of the function.

NOTE

It is good practice to have in mind meaningful estimates of the answer.

Maximizing an Area

A farmer with \(4000 \,{\rm m}\) of fencing wants to enclose a rectangular plot that borders a straight river, as shown in Figure 53. If the farmer does not fence the side along the river, what is the largest rectangular area that can be enclosed?

Figure 53 Area \(A = xy\)

Solution

Step 1 The quantity to be maximized is the area; we denote it by \(A\).

Step 2 We denote the dimensions of the rectangle by \(x\) and \(y\) (both in meters), with the length of the side \(y\) parallel to the river. The area is \( A=xy\). Because there are \(4000 \,{\rm m}\) of fence available, the variables \(x\) and \(y\) are related by the equation \[ \begin{eqnarray*} x+y+x &=&4000 \\[3pt] y &=&4000-2x \end{eqnarray*} \]

Step 3 Now we express the area \(A\) as a function of \(x\). \[ A=A(x) =x(4000-2x)=4000x-2x^{2}\qquad \color{#0066A7}{{\hbox{\(A=xy,\quad y=4000-2x\)}}} \]

The domain of \(A\) is the closed interval \([0,2000]\).

Step 4 To find the number \(x\) that maximizes \(A(x) ,\) we differentiate \(A\) with respect to \(x\) and find the critical numbers: \[ {A}^{\prime }(x)=4000-4x=0 \]

The critical number is \(x=1000\). The maximum value of \(A\) occurs either at the critical number or at an endpoint of the interval \([0,2000]\). \[ A({1000})=2{,}000{,}000\qquad {A(0)=0} \qquad {A({2000})}=0 \]

The maximum value is \(A(1000)=2{,}000{,}000\ {\rm{m}}^{2},\) which results from using a rectangular plot that measures \(2000\ {\rm{m}}\) along the side parallel to the river and \(1000\ {\rm{m}}\) along each of the other two sides.

NOW WORK

Problem 3.

Maximizing a Volume

From each corner of a square piece of sheet metal \(18\) \({\rm{cm}}\) on a side, we remove a small square and turn up the edges to form an open box. What are the dimensions of the box with the largest volume?

Solution

Step 1 The quantity to be maximized is the volume of the box; we denote it by \(V\). We denote the length of each side of the small squares by \(x\) and the length of each side after the small squares are removed by \(y,\) as shown in Figure 54. Both \(x\) and \(y\) are in centimeters.

Figure 54 \(y=18 - 2x\)

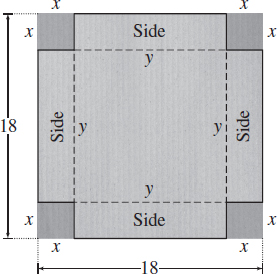
Step 2 Then \(y=( 18-2x) \ {\rm{cm}}\). The height of the box is \(x \ {\rm{cm}}\), and the area of the base of the box is \(y^{2}\ {\rm{cm}}^{2}\). So, the volume of the box is \(V=x{y^{2}}\ {\rm{cm}}^{3}.\)

Step 3 To express \(V\) as a function of one variable, we substitute \( y=18-2x\) into the formula for \(V\). Then the function to be maximized is \[ V=V(x) =x({18-2x})^{2} \]

Since both \(x\geq 0\) and \(18-2x\geq 0,\) we find \(x\leq 9\), meaning the domain of \(V\) is the closed interval \([ 0,9] .\) (All other numbers make no physical sense—do you see why?)

Step 4 To find the value of \(x\) that maximizes \(V\), we differentiate \(V\) and find the critical numbers: \[ {{V^\prime }(x)}=2x({18-2x})({-2})+({18-2x})^{2}=({18-2x})({18-6x}) \]

Now, we solve \(V^\prime (x)=0\) for \(x\). The solutions are \[ x=9\qquad \hbox{or}\qquad x=3 \]

The only critical number in the open interval \((0,9)\) is \(3\). We evaluate \(V\) at \(3\) and at the endpoints \(0\) and \(9\). \[ V(0)=0\qquad V(3)=3(18-6)^{2}=432 \qquad V(9)=0 \]

The maximum volume is \(432\ {\rm{cm}}^{3}\). The box with the maximum volume has a height of \(3\ {\rm{cm}}\). Since \(y=18-2(3) =12\ {\rm{cm}}\), the base of the box measures \(12\ {\rm{cm}}\) by \(12\ {\rm{cm}}\).

NOW WORK

Problem 9.

Maximizing an Area

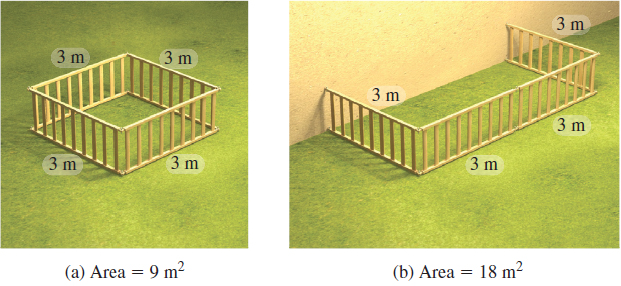
A manufacturer makes a flexible square play yard (Figure 55a), that can be opened at one corner and attached at right angles to a wall or the side of a house, as shown in Figure 55(b). If each side is \(3\ {\rm{m}}\) in length, the open configuration doubles the available area from \(9\ {\rm{m}}^{2}\) to \(18\ {\rm{m}} ^{2}\). Is there a configuration that will more than double the play area?

Figure 55

Solution

Step 1 We want to maximize the play area \(A.\)

Step 2 Since the play yard must be attached at right angles to the wall, the possible configurations depend on the amount of wall used as a fifth side, as shown in Figure 56. We use \(x\) to represent half the length (in meters) of the wall used as the fifth side.

Figure 56

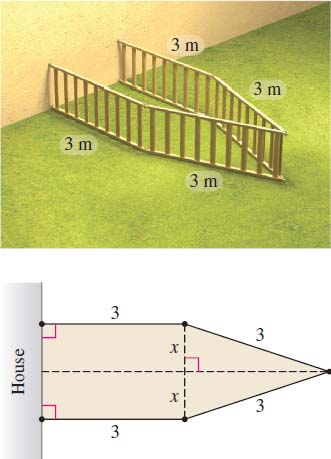
Step 3 We partition the play area into two sections: a rectangle with area \(3(2x) =6x\) and a triangle with base \(2x\) and altitude \( \sqrt{3^{2}-x^{2}}=\sqrt{9-x^{2}}\). The play area \(A\) is the sum of the areas of the two sections. The area to be maximized is \[ A=A(x)=6x+\dfrac{1}{2}( 2x)\sqrt{9-x^{2}} =6x+x\sqrt{9-x^{2}} \]

The domain of \(A\) is the closed interval \([ 0,3].\)

Step 4 To find the maximum area of the play yard, we find the critical numbers of \(A\). \[ \begin{eqnarray*} {A}' (x)&=&6+x\left[ \dfrac{1}{2}( -2x) ( 9-x^{2}) ^{-1/2}\right] +\sqrt{9-x^{2}}\\[5pt] &=&6-\dfrac{x^{2}}{\sqrt{9-x^{2}}}+\sqrt{9-x^{2}} =\frac{6\sqrt{9-x^{2}}-2x^{2}+9}{\sqrt{9-x^{2}}} \end{eqnarray*} \]

Critical numbers occur when \(A^\prime (x) =0\) or where \(A^\prime (x)\) does not exist. \(A^\prime\) does not exist at \(3\), and \(A^\prime (x) =0\) at \[ \begin{eqnarray*} 6\sqrt{9-x^{2}}-2x^{2}+9 &=&0 \\[3pt] \sqrt{9-x^{2}} &=&\dfrac{2x^{2}-9}{6} \\[3pt] 9-x^{2} &=&\left( \dfrac{2x^{2}-9}{6}\right) ^{\!\!2}=\dfrac{4x^{4}-36x^{2}+81}{ 36} \\[3pt] 324-36x^{2} &=&4x^{4}-36x^{2}+81 \\[3pt] 324 &=&4x^{4}+81 \\[3pt] x^{4} &=&\dfrac{324-81}{4}=\dfrac{243}{4} \\[3pt] x &=&\sqrt[{4}]{{\frac{243}{4}}}\approx 2.792 \end{eqnarray*} \]

Figure 57 Area \(\approx\) \(19.817 m^2\)

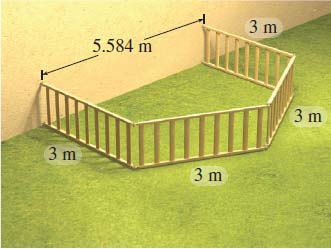
The only critical number in the open interval \((0,3)\) is \(\sqrt[{ 4}]{{ \dfrac{243}{4}}}\approx 2.792\).

Now we evaluate \(A(x)\) at the endpoints \(0\) and \(3\) and at the critical number \( x\approx 2.792\). \[ A(0)=0\qquad A(3)=18\qquad A({2.792})\approx 19.817 \]

Using a wall of length \(2x\approx 2( 2.792) =5.584\ {\rm{m}}\) will maximize the area; the configuration shown in Figure 57 increases the play area by about \(10\%\) (from \(18\) to \(19.817\ {\rm{m}}^{2}\)).

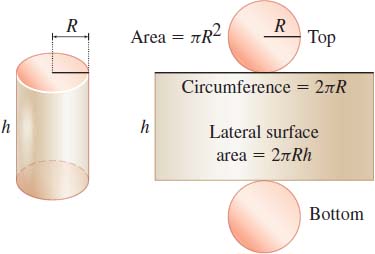
Minimizing Cost

A manufacturer needs to produce a cylindrical container with a capacity of \( 1000\ {\rm{cm}}^{3}\). The top and bottom of the container are made of material that costs $0.05 per square centimeter, while the sides of the container are made of material costing $0.03 per square centimeter. Find the dimensions that will minimize the company’s cost of producing the container.

Solution Figure 58 shows a cylindrical container and the area of its top, bottom, and lateral surfaces. As shown in the figure, we let \(h\) denote the height of the container and \(R\) denote the radius. The total area of the bottom and top is \(2\pi\! R^{2}\ {\rm{cm}}^{2}\). The area of the lateral surface of the can is \(2\pi\! Rh\ {\rm{cm}}^{2}\).

The variables \(h\) and \(R\) are related. Since the volume of the cylinder is \( 1000\ {\rm{cm}}^{3}\), \[ \begin{eqnarray*} V &=&\pi\! R^{2}h=1000 \\[3pt] h &=&\frac{1000}{\pi\! R^{2}} \end{eqnarray*} \]

The cost \(C\), in dollars, of manufacturing the container is \[ C=(0.05)({2\pi\! R^{2}})+(0.03)({2\pi\! Rh})=0.1\pi\! R^{2}+0.06\pi\! Rh \]

By substituting for \(h\), we can express \(C\) as a function of \(R\). \[ C=C( R) =0.1\pi\! R^{2}+({0.06\pi\! R})\left( {\frac{1000}{\pi\! R^{2}}} \right)\! =0.1\pi\! R^{2}+\frac{60}{R} \]

This is the function to be minimized. The domain of \(C\) is \(\left\{ R|R>0\right\}\).

To find the minimum cost, we differentiate \(C\) with respect to \(R\). \[ {C}' (R)=0.2\pi\! R-\frac{60}{R^{2}}=\frac{0.2\pi\! R^{3}-60}{R^{2}} \]

Solve \(C' (R)=0\) to find the critical numbers. \[ \begin{eqnarray*} 0.2\pi\! R^{3}-60 &=&0 \\[1pt] R^{3} &=&\frac{300}{\pi } \\[1pt] R &=&\sqrt[3]{\frac{300}{\pi }}\approx 4.571\,\ {\rm{cm}} \end{eqnarray*} \]

Now we find \(C'' (x)\) and use the Second Derivative Test. \[ \begin{eqnarray*} {C}'' (R) &=&0.2\pi +\frac{120}{R^{3}} \\[3pt] {C}'' \left( \sqrt[3]{\frac{300}{\pi }}\right) &=&0.2\pi +\frac{ 120\pi }{300}=0.6\pi >0 \end{eqnarray*} \]

\(C\) has a local minimum at \(\sqrt[3]{\dfrac{300}{\pi }}\). Since \(C'' (R)>0\) for all \(R\) in the domain, the graph of \(C\) is always concave up, and the local minimum value is the absolute minimum value. The radius of the container that minimizes the cost is \(R\approx 4.571\ {\rm{cm}}.\) The height of the container that minimizes the cost of the material is \[ h=\frac{1000}{\pi\! R^{2}}\approx \frac{1000}{20.892\pi }\approx 15.236\,\ {\rm{cm}} \]

The minimum cost of the container is \[ C\left( \sqrt[3]{\dfrac{300}{\pi }} \right) =0.1\pi \left( \sqrt[3]{\dfrac{300}{\pi }}\right) ^{2}+\dfrac{60}{ \sqrt[3]{\dfrac{300}{\pi }}}\approx \$19.69. \]

NOW WORK

Problem 11.

Maximizing Area

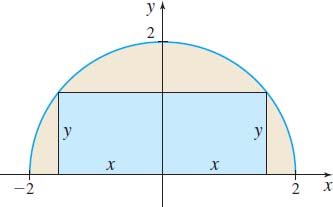
A rectangle is inscribed in a semicircle of radius \(2\). Find the dimensions of the rectangle that has the maximum area.

Solution We present two methods of solution: The first uses analytic geometry, the second uses trigonometry. To begin, we place the semicircle with its diameter along the \(x\)-axis and center at the origin. Then we inscribe a rectangle in the semicircle, as shown in Figure 59. The length of the inscribed rectangle is \(2x\) and its height is \(y.\)

Figure 59

Analytic Geometry Method The area \(A\) of the inscribed rectangle is \(A=2xy\) and the equation of the semicircle is \(x^{2}+y^{2}=4\), \(y\geq 0.\) We solve for \(y\) in \(x^{2}+y^{2}=4\) and obtain \(y=\sqrt{4-x^{2}}\). Now we substitute this expression for \(y\) in the area formula for the rectangle to express \(A\) as a function of \(x\) alone. \[ \begin{eqnarray*} A&=&A(x)= 2x\sqrt{4-x^{2}}\qquad 0\leq x\leq 2\\[-6.4pt] &&\hspace{-1.8pc}\color{#0066A7}{\underset{\hbox{\(A=2xy; y=\sqrt{4-x^{2}}\)}}{\uparrow}} \end{eqnarray*} \]

Then \[ \begin{eqnarray*} {A}' (x) &=&2\left[ x\left( {{\dfrac{1}{2}}}\right) \ (4-x^{2}) ^{-1/2}(-2x)+\sqrt{4-x^{2}}\right] =2\left[ \dfrac{-x^{2}}{ \sqrt{4-x^{2}}}+\sqrt{4-x^{2}}\right]\\[3pt] &=&2\left[ \frac{-x^{2}+( {4-x^{2}}) }{\sqrt{4-x^{2}}}\right] =2\left[ \frac{-2({x^{2}-2})}{\sqrt{4-x^{2}}}\right] =-\frac{4({x^{2}-2})}{\sqrt{4-x^{2}}} \end{eqnarray*} \]

The only critical number in the open interval \((0,2)\) is \(\sqrt{2}\), where \( A^\prime ( \sqrt{2}) =0.\) [\(-\sqrt{2}\) and \(-2\) are not in the domain of \(A\), and \(2\) is not in the open interval \(( 0,2)\).] The values of \(A\) at the endpoints \(0\) and \(2\) and at the critical number \(\sqrt{2}\) are \[ A(0)=0\qquad A(\sqrt{2})=4\qquad A(2)=0 \]

The maximum area of the inscribed rectangle is \(4\), and it corresponds to the rectangle whose length is \(2x=2\sqrt{2}\) and whose height is \(y=\sqrt{2}\).

Figure 60

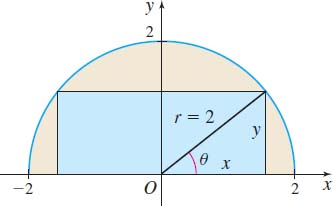
Trigonometric Method Using Figure 59, we draw the radius \(r=2\) from \(O\) to the vertex of the rectangle and place the angle \(\theta\) in the standard position, as shown in Figure 60. Then \(x=2\cos \theta\) and \(y=2\sin \theta ,\) \(0\leq \theta \leq \dfrac{\pi }{2}\). The area \(A\) of the rectangle is \[ \begin{eqnarray*} A&=&2xy=2(2\, \cos \theta )(2\, \sin\, \theta )=8\, \cos \theta\, \sin\, \theta \underset{\underset{{\color{#0066A7}{\hbox{\(\sin (2\theta) =2\, \sin\, \theta \cos \theta\)}}}}{\color{#0066A7}{\uparrow}}}{=} 4\sin ( 2\, \theta )\\[-6.3pt] \end{eqnarray*} \]

Since the area \(A\) is a differentiable function of \(\theta\), we obtain the critical numbers by finding \(A^\prime (\theta )\) and solving the equation \(A^\prime (\theta ) =0\). \[ \begin{eqnarray*} A^\prime (\theta ) &=&8\, \cos ( 2\theta ) =0 \\[1pt] \cos ( 2\theta ) &=&0 \\[1pt] 2\theta &=&\cos ^{-1}0=\dfrac{\pi }{2} \\[3pt] \theta &=&\dfrac{\pi }{4} \end{eqnarray*} \]

We now find \(A^{\prime \prime} (\theta )\) and use the Second Derivative Test. \[ \begin{eqnarray*} {A}'' (\theta )&=&-16\, \sin ( 2\theta ) \\[3pt] {A}'' \left( {\dfrac{\pi }{4}}\right) &=&-16\, \sin \left( 2\cdot \dfrac{\pi }{4}\right) =-16\, \sin \dfrac{\pi }{2}=-16<0 \end{eqnarray*} \]

So at \(\theta =\dfrac{\pi }{4}\), the area \(A\) is maximized and the maximum area of the inscribed rectangle is \[ A\left( \dfrac{\pi }{4}\right) =4\sin \left( 2\cdot \frac{\pi }{4}\right) =4 \hbox{ square units} \]

The rectangle with the maximum area has \[ \hbox{length}\, 2x=4\cos \dfrac{\pi }{4}=2 \sqrt{2}\,\, \hbox{and height}\,\, y=2\, \sin \dfrac{\pi }{4} =\sqrt{2} \]

NOW WORK

Problem 41.

ORIGINS

In 1621 Willebrord Snell (c. 1580–1626) discovered the law of refraction, one of the basic principles of geometric optics. Pierre de Fermat (1601–1665) was able to prove the law mathematically using the principle that light follows the path that takes the least time.

Snell’s Law of Refraction

Light travels at different speeds in different media (air, water, glass, etc.) Suppose that light travels from a point \(A\) in one medium, where its speed is \(c_{1}\), to a point \(B\) in another medium, where its speed is \( c_{2}.\) See Figure 61. We use Fermat’s principle that light always travels along the path that requires the least time to prove Snell’s Law of Refraction. \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\frac{{\sin {\theta _1}}}{{{c_1}}} = \frac{{\sin {\theta _2}}}{{{c_2}}}}}\]

Figure 61

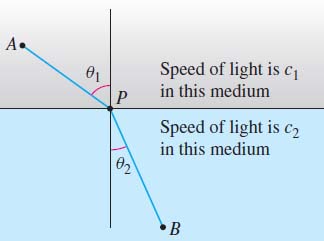
Solution We position the coordinate system, as illustrated in Figure 62. The light passes from one medium to the other at the point \(P\). Since the shortest distance between two points is a line, the path taken by the light is made up of two line segments—from \(A=( 0,a)\) to \( P=( x,0)\) and from \(P=( x,0)\) to \(B=(k,-b)\), where \(a, b\), and \(k\) are positive constants.

Figure 62

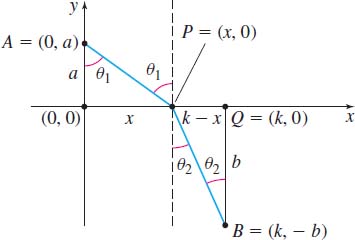
Since \[ \hbox{Time}= \dfrac{{\rm Distance}}{{\rm Speed }} \]

the travel time \(t_{1}\) from \(A=( 0,a)\) to \(P=( x,0)\) is \[ t_{1}=\frac{\sqrt{x^{2}+a^{2}}}{c_{1}} \]

and the travel time \(t_{2}\) from \(P=( x,0)\) to \(B=( k,-b)\) is \[ t_{2}=\frac{\sqrt{(k-x)^{2}+b^{2}}}{c_{2}} \]

The total time \(T=T(x)\) is given by \[ T(x) =t_{1}+t_{2}=\frac{\sqrt{x^{2}+a^{2}}}{c_{1}}+\frac{\sqrt{({k-x})^{2}+b^{2}}}{c_{2}} \]

To find the least time, we find the critical numbers of \(T.\) \[ \begin{equation} T' (x) =\frac{x}{c_{1}\sqrt{x^{2}+a^{2}}}-\frac{k-x}{c_{2} \sqrt{({k-x})^{2}+b^{2}}}=0 \tag{1} \end{equation} \]

From Figure 62, \[ \begin{equation} {\frac{x}{\sqrt{x^{2}+a^{2}}}=\sin\, \theta _{1}}\qquad \hbox{and}\qquad { \frac{k-x}{\sqrt{({k-x})^{2}+b^{2}}}=\sin\, \theta _{2}} \tag{2} \end{equation} \]

Using the result from (2) in equation (1), we have \[ \begin{eqnarray*} T' (x) = \frac{\sin\, \theta _{1}}{c_{1}}-{\frac{\sin\, \theta _{2}}{c_{2}}} &=&0 \\[3pt] {\frac{\sin\, \theta _{1}}{c_{1}}} &=&{\frac{\sin\, \theta _{2}}{c_{2}}} \end{eqnarray*} \]

Now to ensure that the minimum value of \(T\) occurs when \(T' (x)=0\), we show that \(T'' (x) >0\). From (1), \[ \begin{eqnarray*} {T'' }(x) &=&{\frac{d}{dx}\left[ {\frac{x}{c_{1}\sqrt{ x^{2}+a^{2}}}}\right] -\frac{d}{dx}\left[ {\frac{k-x}{c_{2}\sqrt{({k-x} )^{2}+b^{2}}}}\right] } \\[3pt] &=&{\frac{a^{2}}{c_{1}({x^{2}+a^{2}})^{3/2}}+\frac{b^{2} }{c_{2}[{({k-x})^{2}+b^{2}}]^{3/2}}>0} \end{eqnarray*} \]

Since \(T'' (x) >0\) for all \(x,\) \(T\) is concave up for all \(x,\) and the minimum value of \(T\) occurs at the critical number. That is, \(T\) is a minimum when \(\dfrac{\sin\, \theta _{1}}{c_{1}}=\dfrac{\sin\, \theta _{2}}{c_{2}}\).