Question

Maximizing Area The owner of a motel has \(3000\ {\rm{m}}\) of fencing and wants to enclose a rectangular plot of land that borders a straight highway. If she does not fence the side along the highway, what is the largest area that can be enclosed?

Question

Maximizing Area If the motel owner in Problem 1 decides to also fence the side along the highway, except for \(5\ {\rm{m}}\) to allow for access, what is the largest area that can be enclosed?

Question

Maximizing Area Find the dimensions of the rectangle with the largest area that can be enclosed on all sides by \(L\) meters of fencing.

Question

Maximizing the Area of a Triangle An isosceles triangle has a perimeter of fixed length \(L\). What should the dimensions of the triangle be if its area is to be a maximum? See the figure.

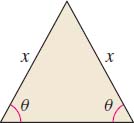
Question

Maximizing Area A gardener with \(200\ {\rm{m}}\) of available fencing wishes to enclose a rectangular field and then divide it into two plots with a fence parallel to one of the sides, as shown in the figure. What is the largest area that can be enclosed?

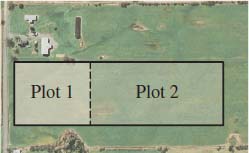
Question

Minimizing Fencing A realtor wishes to enclose \(600\ {\rm{m}} ^{2}\) of land in a rectangular plot and then divide it into two plots with a fence parallel to one of the sides. What are the dimensions of the rectangular plot that require the least amount of fencing?

Question

Maximizing the Volume of a Box An open box with a square base is to be made from a square piece of cardboard that measures \(12\ {\rm{cm}}\) on each side. A square will be cut out from each corner of the cardboard and the sides will be turned up to form the box. Find the dimensions that yield the maximum volume.

Question

Maximizing the Volume of a Box An open box with a rectangular base is to be made from a piece of tin measuring \(30\ {\rm{cm}}\) by \(45\ {\rm{cm}}\) by cutting out a square from each corner and turning up the sides. Find the dimensions that yield the maximum volume.

Question

Minimizing the Surface Area of a Box An open box with a square base is to have a volume of \(2000\ {\rm{cm}}^{3}\). What should the dimensions of the box be if the amount of material used is to be a minimum?

Question

Minimizing the Surface Area of a Box If the box in Problem 9 is to be closed on top, what should the dimensions of the box be if the amount of material used is to be a minimum?

Question

Minimizing the Cost to Make a Can A cylindrical container that has a capacity of \(10\ {\rm{m}}^{3}\) is to be produced. The top and bottom of the container are to be made of a material that costs \({\$}20\) per square meter, while the side of the container is to be made of a material costing \({\$}15\) per square meter. Find the dimensions that will minimize the cost of the material.

Question

Minimizing the Cost of Fencing A builder wishes to fence in \(60,000\ {\rm{m}}^{2}\) of land in a rectangular shape. For security reasons, the fence along the front part of the land will cost \({\$}20\) per meter, while the fence for the other three sides will cost \({\$}10\) per meter. How much of each type of fence should the builder buy to minimize the cost of the fence? What is the minimum cost?

Question

Maximizing Revenue A car rental agency has \(24\) cars (each an identical model). The owner of the agency finds that at a price of \({\$}18\) per day, all the cars can be rented; however, for each \({\$}1\) increase in rental cost, one of the cars is not rented. What should the agency charge to maximize income?

Question

Maximizing Revenue A charter flight club charges its members \({\$}200\) per year. But for each new member in excess of \(60\), the charge for every member is reduced by \({\$}2\). What number of members leads to a maximum revenue?

Question

Minimizing Distance Find the coordinates of the points on the graph of the parabola \(y=x^{2}\) that are closest to the point \(\left( 2, \dfrac{1}{2}\right)\).

Question

Minimizing Distance Find the coordinates of the points on the graph of the parabola \(y\) \(=2x^{2}\) that are closest to the point \(( 1,4)\).

Question

Minimizing Distance Find the coordinates of the points on the graph of the parabola \(y=4-x^{2}\) that are closest to the point \((6,2)\).

326

Question

Minimizing Distance Find the coordinates of the points on the graph of \(y=\sqrt{x}\) that are closest to the point \((4,0)\).

Question

Minimizing Transportation Cost A truck has a top speed of \( 75\) mi/h and, when traveling at a speed of \(x\ {\rm mi}/{\rm h}\), consumes gasoline at the rate of \(\dfrac{1}{200}\left[ \dfrac{{1600} }{x} +x\right]\) gallons per mile. The truck is to be taken on a 200-\({\rm mi}\) trip by a driver who is paid at the rate of \({\$}b\) per hour plus a commission of \({\$}c\). Since the time required for the trip at \(x~{\rm mi}/{\rm h}\) is \(\dfrac{200}{x}\), the cost \(C\) of the trip, when gasoline costs \({\$}a\) per gallon, is \[ C=C(x)=\left( {\frac{1600}{x}+x}\right) \ a+\frac{200}{x}b+c \]

Find the speed that minimizes the cost \(C\) under each of the following conditions:

1. \(a={\$}3.50\), \(b=0\), \(c=0\)
2. \(a={\$}3.50\), \(b={\$}10.00\), \(c={\$}500\)
3. \(a={\$}4.00\), \(b={\$}20.00\), \(c=0\)

Question

Optimal Placement of a Cable Box A telephone company is asked to provide cable service to a customer whose house is located \(2\ {\rm{km}}\) away from the road along which the cable lines run. The nearest cable box is located \(5\ {\rm{km}}\) down the road. As shown in the figure below, let \(5-x\) denote the distance from the box to the connection so that \(x\) is the distance from this point to the point on the road closest to the house. If the cost to connect the cable line is \({\$}500\) per kilometer along the road and \({\$}600\) per kilometer away from the road, where along the road from the box should the company connect the cable line so as to minimize construction cost?

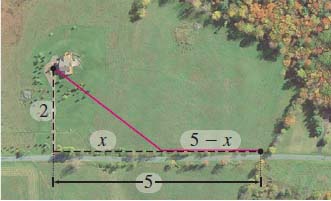
Question

Minimizing a Path Two houses \(A\) and \(B\) on the same side of a road are a distance \(p\) apart, with distances \(q\) and \(r\), respectively, from the center of the road, as shown in the figure below. Find the length of the shortest path that goes from \(A\) to the road and then on to the other house \(B\).

1. Use calculus.
2. Use only elementary geometry.

(Hint: Reflect \(B\) across the road to a point \(C\) that is also a distance \(r\) from the center of the road.)

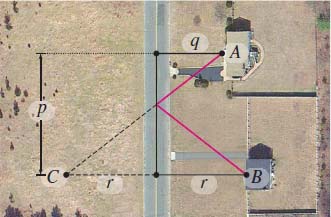
Question

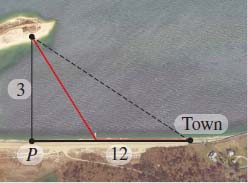
Minimizing Travel Time A small island is \(3\ {\rm{km}}\) from the nearest point \(P\) on the straight shoreline of a large lake. A town is \( 12\ {\rm{km}}\) down the shore from \(P\). See the figure. If a person on the island can row a boat \(2.5\ {\rm{km}}/\ {\rm{h}}\) and can walk \(4\ {\rm{km}}/\ {\rm{h}}\), where should the boat be landed so that the person arrives in town in the shortest time?

Question

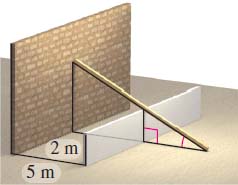
Supporting a Wall Find the length of the shortest beam that can be used to brace a wall if the beam is to pass over a second wall \(2 \ {\rm{m}}\) high and \(5\ {\rm{m}}\) from the first wall. See the figure. What is the angle of elevation of the beam?

Question

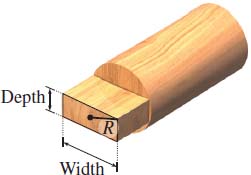
Maximizing the Strength of a Beam The strength of a rectangular beam is proportional to the product of the width and the cube of its depth. Find the dimensions of the strongest beam that can be cut from a log whose cross section has the form of a circle of fixed radius \(R\). See the figure.

Question

Maximizing the Strength of a Beam If the strength of a rectangular beam is proportional to the product of its width and the square of its depth, find the dimensions of the strongest beam that can be cut from a log whose cross section has the form of the ellipse \(10x^{2}+9y^{2}=90\). (Hint: Choose width \(=2x\) and depth \(=2y\).)

Question

Maximizing the Strength of a Beam The strength of a beam made from a certain wood is proportional to the product of its width and the cube of its depth. Find the dimensions of the rectangular cross section of the beam with maximum strength that can be cut from a log whose original cross section is in the form of the ellipse \(b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}\), \(a\geq b\).

Question

Pricing Wine A winemaker in Walla Walla, Washington, is producing the first vintage for her own label, and she needs to know how much to charge per case of wine. It costs her \(\$132\) per case to make the wine. She understands from industry research and an assessment of her marketing list that she can sell \(x=1430-\dfrac{11}{6}p\) cases of wine, where \(p\) is the price of a case in dollars. She can make at most \(1100\) cases of wine in her production facility. How many cases of wine should she produce, and what price \(p\) should she charge per case to maximize her profit \(P\)? (Hint: Maximize the profit \(P=xp-132x,\) where \(x\) equals the number of cases.)

327

Question

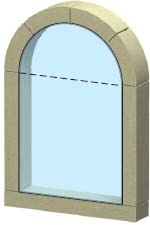
Optimal Window Dimensions A Norman window has the shape of a rectangle surmounted by a semicircle of diameter equal to the width of the rectangle, as shown in the figure. If the perimeter of the window is \(10\ {\rm{ m}}\), what dimensions will admit the most light?

Question

Maximizing Volume The sides of a V-shaped trough are \(28\ {\rm{cm}}\) wide. Find the angle between the sides of the trough that results in maximum capacity.

Question

Maximizing Volume A metal rain gutter is to have 10-\(\!\ {\rm{cm}}\) sides and a 10-\(\!\ {\rm{cm}}\) horizontal bottom, with the sides making equal angles with the bottom, as shown in the figure. How wide should the opening across the top be for maximum carrying capacity?

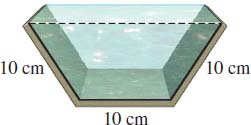
Question

Minimizing Construction Cost A proposed tunnel with a fixed cross-sectional area is to have a horizontal floor, vertical walls of equal height, and a ceiling that is a semicircular cylinder. If the ceiling costs three times as much per square meter to build as the vertical walls and the floor, find the most economical ratio of the diameter of the semicircular cylinder to the height of the vertical walls.

Question

Minimizing Construction Cost An observatory is to be constructed in the form of a right circular cylinder surmounted by a hemispherical dome. If the hemispherical dome costs three times as much per square meter as the cylindrical wall, what are the most economical dimensions for a given volume? Neglect the floor.

Question

Intensity of Light The intensity of illumination at a point varies inversely as the square of the distance between the point and the light source. Two lights, one having an intensity eight times that of the other, are \(6\ {\rm{m}}\) apart. At what point between the two lights is the total illumination least?

Question

Drug Concentration The concentration of a drug in the bloodstream \(t\) hours after injection into muscle tissue is given by \( C(t) =\dfrac{2t}{16+t^{2}}\). When is the concentration greatest?

Question

Optimal Wire Length A wire is to be cut into two pieces. One piece will be bent into a square, and the other piece will be bent into a circle. If the total area enclosed by the two pieces is to be \(64\ {\rm{cm}} ^{2}\), what is the minimum length of wire that can be used? What is the maximum length of wire that can be used?

Question

Optimal Wire Length A wire is to be cut into two pieces. One piece will be bent into an equilateral triangle, and the other piece will be bent into a circle. If the total area enclosed by the two pieces is to be \(64\ {\rm{cm}}^{2}\), what is the minimum length of wire that can be used? What is the maximum length of wire that can be used?

Question

Optimal Area A wire \(35\ {\rm{cm}}\) long is cut into two pieces. One piece is bent into the shape of a square, and the other piece is bent into the shape of a circle.

1. How should the wire be cut so that the area enclosed is a minimum?
2. How should the wire be cut so that the area enclosed is a maximum?
3. Graph the area enclosed as a function of the length of the piece of wire used to make the square. Show that the graph confirms the results of (a) and (b).

Question

Optimal Area A wire \(35\ {\rm{cm}}\) long is cut into two pieces. One piece is bent into the shape of an equilateral triangle, and the other piece is bent into the shape of a circle.

1. How should the wire be cut so that the area enclosed is a minimum?
2. How should the wire be cut so that the area enclosed is a maximum?
3. Graph the area enclosed as a function of the length of the piece of wire used to make the triangle. Show that the graph confirms the results of (a) and (b).

Question

Optimal Dimensions for a Can Show that a cylindrical container of fixed volume \(V\) requires the least material (minimum surface area) when its height is twice its radius.

Question

Maximizing Area Find the triangle of largest area that has two sides along the positive coordinate axes if its hypotenuse is tangent to the graph of \(y=3e^{-x}\).

Question

Maximizing Area Find the largest area of a rectangle with one vertex on the parabola \(y=9-x^{2}\), another at the origin, and the remaining two on the positive \(x\)-axis and positive \(y\) -axis, respectively. See the figure.

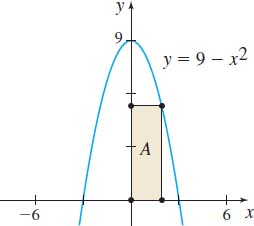
Question

Maximizing Volume Find the dimensions of the right circular cone of maximum volume having a slant height of 4 ft. See the figure.

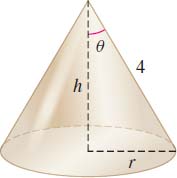
Question

Minimizing Distance Let \(a\) and \(b\) be two positive real numbers. Find the line through the point \((a,b)\) and connecting the points \( (0,y_{0})\) and \((x_{0},0)\) so that the distance from \(( x_{0},0)\) to \(( 0,y_{0})\) is a minimum. (In general, \(x_{0}\) and \(y_{0}\) will depend on the line.)

Question

Maximizing Velocity An object moves on the \(x\)-axis in such a way that its velocity at time \(t\) seconds, \(t\ge 1\), is given by \(v=\) \(\dfrac{\ln t}{t}\ {\rm{cm}}/ {\rm{s}}\). At what time \(t\) does the object attain its maximum velocity?

328

Question

Physics A heavy object of mass \(m\) is to be dragged along a horizontal surface by a rope making an angle \(\theta\) to the horizontal. The force \(F\) required to move the object is given by the formula \[ F=\frac{cmg}{c\, \sin\, \theta +\cos \theta } \]

where \(g\) is the acceleration due to gravity and \(c\) is the coefficient of friction of the surface. Show that the force is least when \(\tan \theta =c\).

Question

Chemistry A self-catalytic chemical reaction results in the formation of a product that causes its formation rate to increase. The reaction rate \(V\) of many self-catalytic chemicals is given by \[ {V=kx({a-x})}\qquad {0\leq x\leq a} \]

where \(k\) is a positive constant, \(a\) is the initial amount of the chemical, and \(x\) is the variable amount of the chemical. For what value of \(x\) is the reaction rate a maximum?

Question

Optimal Viewing Angle A picture \(4\ {\rm{m}}\) in height is hung on a wall with the lower edge \(3\ {\rm{m}}\) above the level of an observer’s eye. How far from the wall should the observer stand in order to obtain the most favorable view? (That is, the picture should subtend the maximum angle.)

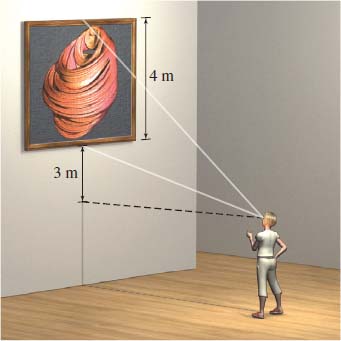
Question

Maximizing Transmission Speed Traditional telephone cable is made up of a core of copper wires covered by an insulating material. If \( x\) is the ratio of the radius of the core to the thickness of the insulating material, the speed \(v\) of signaling is \(v=kx^{2}\ln \dfrac{1}{x },\) where \(k\) is a constant and \(x\) is greater than or equal to 1. Determine the ratio \(x\) that results in maximum speed.

Question

Absolute Minimum If \(a\), \(b\), and \(c\) are positive constants, show that the minimum value of \(f(x)=ae^{cx}+be^{-cx}\) is \(2\sqrt{ab}\).

Question

Maximizing Length The figure shows two corridors meeting at a right angle. One has width \(1\ {\rm{m}}\), and the other, width \(8\ {\rm{m}}\). Find the length of the longest pipe that can be carried horizontally from one corridor, around the corner, and into the other corridor.

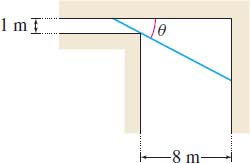
Question

Optimal Height of a Lamp In the figure, a circular area of radius \(20\ {\rm{ft}}\) is surrounded by a walk. A light is placed above the center of the area. What height most strongly illuminates the walk? The intensity of illumination is given by \(I=\dfrac{\sin\, \theta }{s}\), where \(s\) is the distance from the source and \(\theta\) is the angle at which the light strikes the surface.

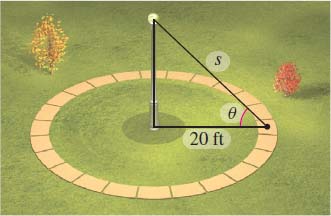
Question

Maximizing Area Show that the rectangle of largest area that can be inscribed under the graph of \(y=e^{-x^{2}}\) has two of its vertices at the point of inflection of \(y\). See the figure.

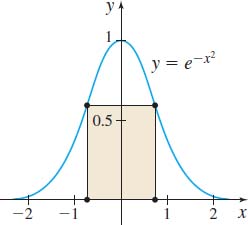
Question

Minimizing Distance Find the point \(( x,y)\) on the graph of \(f(x) =e^{-x/2}\) that is closest to the point \(( 1,8).\)