4.8 Antiderivatives; Differential Equations
OBJECTIVES
When you finish this section, you should be able to:
- Find antiderivatives (p. 329)
- Solve a differential equation (p. 331)
- Solve applied problems modeled by differential equations (p. 333)
We have already learned that for each differentiable function \(f,\) there is a corresponding derivative function \(f^\prime\). We now consider the question: For a given function \(f\), can we find a function \(F\) whose derivative is \(f\)? That is, is it possible to find a function \(F\) so that \(F^\prime =\dfrac{dF}{dx}=f\)? If such a function \(F\) can be found, it is called an antiderivative of \(f\).
329
spanDEFINITIONspan Antiderivative
A function \(F\) is called an antiderivative of the function \(f\) if \(F^\prime (x) = f(x)\) for all \(x\) in the domain of \(f\).
1 Find Antiderivatives
For example, an antiderivative of the function \(f(x) =2x\) is \(F(x) =x^{2}\), since \[ F^\prime (x) = \frac{d}{dx}x^{2} = 2x \]
Another function \(F\) whose derivative is \(2x\) is \(F(x) =x^{2}+3\), since \[ F^\prime (x) =\frac{d}{dx}(x^{2}+3)=2x \]
This leads us to suspect that the function \(f(x)=2x\) has many antiderivatives. Indeed, any of the functions \(x^{2}\) or \(x^{2}+\dfrac{1}{2}\) or \(x^{2}+2\) or \(x^{2}+\sqrt{5}\) or \(x^{2}-1\) has the property that its derivative is \(2x\). Any function \(F(x) =x^{2}+C\), where \(C\) is a constant, is an antiderivative of \(f(x) =2x\).
Are there other antiderivatives of \(2x\) that are not of the form \(x^{2}+C?\) A corollary of the Mean Value Theorem (p. 279) tells us the answer is no.
COROLLARY
If \(f\) and \(g\) are differentiable functions and if \(f^\prime (x) =g^\prime (x)\) for all numbers \(x\) in an interval \((a,b),\) then there exists a number \(C\) for which \(f(x) =g(x) +C\) on \((a,b)\).
This result can be stated in the following way.
THEOREM
If a function \(F\) is an antiderivative of a function \(f\) defined on an interval \(I\), then any other antiderivative of \(f\) has the form \(F(x) +C\), where \(C\) is an (arbitrary) constant.
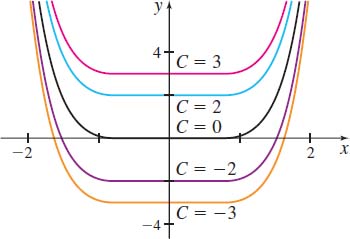
All the antiderivatives of \(f\) can be obtained from the expression \(F(x)+C\) by letting \(C\) range over all real numbers. For example, all the antiderivatives of \(f(x) =x^{5}\) are of the form \(F(x) =\dfrac{x^{6}}{6}+C\), where \(C\) is a constant. Figure 64 shows the graphs of \(F(x) =\dfrac{x^{6}}{6}+C\) for some numbers \(C.\) The antiderivatives of a function \(f\) are a family of functions, each one a vertical translation of the others.
Finding the Antiderivatives of a Function
Find all the antiderivatives of:
- \(f(x) =0\)
- \(g(\theta ) =-\sin \theta\)
- \(h(x)=x^{1/2}\)
Solution (a) Since the derivative of a constant function is \(0,\) all the antiderivatives of \(f\) are of the form \(F(x) =C,\) where \(C\) is a constant.
(b) Since \(\dfrac{d}{d\theta}\cos \theta = -\sin \theta\), all the antiderivatives of \(g(\theta) = -\sin \theta\) are of the form \(G(\theta ) =\cos \theta +C\).
330
(c) The derivative of \(\dfrac{2}{3}x^{3/2}\) is \(\left( \dfrac{2}{3}\right) \ \left( \dfrac{3}{2}x^{\hbox{$\frac{3}{2}-1$}}\right) =x^{1/2}\).
So, all the antiderivatives of \(h(x)=x^{1/2}\) are of the form \(H(x) ={{\dfrac{2}{3}}x^{3/2}+C}\), where \({C}\) is a constant.
In Example 1(c), you may wonder how we knew to choose \({\dfrac{2}{3}}x^{3/2}\). For any real number \(a\), the Power Rule states \(\dfrac{d}{dx} x^{a}=ax^{a-1}\). That is, differentiation reduces the exponent by \(1\). Antidifferentiation is the inverse process, so it suggests we increase the exponent by \(1\). This is how we obtain the factor \(x^{3/2}\) of the antiderivative \({\dfrac{2}{3}}x^{3/2}\). The factor \({\dfrac{2}{3}}\) is needed so that when we differentiate \(\dfrac{2}{3}x^{3/2}\), the result is \(\dfrac{2}{3}\cdot \dfrac{3}{2}x^{{\frac{3}{2}}-1} =x^{1/2}\).
NOW WORK
Problem 17.
Let \(f(x)=x^{a}\), where \(a\) is a real number and \(a\neq -1\). (The case for which \(a=-1\) requires special attention.) Then the function \(F(x)\) defined by \[ F(x)=\dfrac{x^{{ a}+1}}{a+1}\,\, \ \ \, a\ne -1 \]
is an antiderivative of \(f(x)=x^{a}\). That is, all the antiderivatives of \(f(x) =x^{a}\), \(a\neq -1\), are of the form \(\dfrac{x^{{a}+1}}{a+1}+C\), where \(C\) is a constant.
Now we consider the case when \(a=-1\). We know that \(\dfrac{d}{dx}\ln \vert x\vert =\dfrac{1}{x}=x^{-1}\), for \(x\neq 0\). So, all the antiderivatives of \(f(x) =x^{-1}\) are of the form \(\ln \vert x\vert +C\), provided \( x\neq 0.\)
Table 6 includes these results along with the antiderivatives of some other common functions.
| Function f | Antiderivatives F of f | Function f | Antiderivatives F of f |
|---|---|---|---|
| \(f(x) =0\) | \(F(x) =C\) | \(f(x) =\sec x\tan x\) | \(F(x) =\sec x+C\) |
| \(f(x) =1\) | \(F(x) =x+C\) | \(f(x) =\csc x\cot x\) | \(F(x) =-\csc x+C\) |
| \(f(x) =x^{a},\quad a\neq -1\) | \(F(x) =\dfrac{x^{a+1}}{a+1}+C\) | \(f(x) =\csc ^{2}x\) | \(F(x) =-\cot x+C\) |
| \(f(x) =x^{-1}=\dfrac{1}{x}\) | \(F(x) =\ln \vert x\vert +C\) | \(f(x) =\dfrac{1}{\sqrt{1-x^{2}}},\) \(\vert x\vert <1\) | \(F(x) =\sin ^{-1}x+C\) |
| \(f(x) =e^{x}\) | \(F(x) =e^{x}+C\) | \(f(x) =\dfrac{1}{1+x^{2}}\) | \(F(x) =\tan ^{-1}x+C\) |
| \(f(x) =a^{x}\) | \(F(x) =\dfrac{a^{x}}{\ln a}+C,\) \(a>0, a\neq 1\) | \(f(x) =\dfrac{1}{x\sqrt{x^{2}-1}},\) \(\vert x\vert >1\) | \(F(x) =\sec^{-1}x+C\) |
| \(f(x) =\sin x\) | \(F(x) =-\cos x+C\) | \(f(x) =\sinh x\) | \(F(x) =\cosh x+C\) |
| \(f(x) =\cos x\) | \(F(x) =\sin x+C\) | \(f(x) =\cosh x\) | \(F(x) =\sinh x+C\) |
| \(f(x) =\sec^{2}x\) | \(F(x) =\tan x+C\) |
The next two theorems are consequences of the properties of derivatives and the relationship between derivatives and antiderivatives.
IN WORDS
An antiderivative of the sum of two functions equals the sum of the antiderivatives of the functions.
THEOREM Sum Rule
If the functions \(F_{1}\) and \(F_{2}\) are antiderivatives of the functions \(f_{1}\) and \(f_{2}\), respectively, then \(F_{1}+F_{2}\) is an antiderivative of \(f_{1}+f_{2}\).
331
The Sum Rule can be extended to any finite sum of functions. A similar result is also true for differences.
IN WORDS
An antiderivative of a number times a function equals the number times an antiderivative of the function.
THEOREM Constant Multiple Rule
If \(k\) is a real number and if \(F\) is an antiderivative of \(f\), then \(kF\) is an antiderivative of \(kf\).
Finding the Antiderivatives of a Function
Find all the antiderivatives of \(f(x)=e^{x}+\dfrac{6}{x^{2}}-\sin x\).
Solution Since \(f\) is the sum of three functions, we use the Sum Rule. That is, we find the antiderivatives of each function individually and then add. \[ f(x) =e^{x}+6x^{-2}-\sin x \]
NOTE
Since the antiderivatives of \(e^{x}\) are \(e^{x}+{C}_{1}\), the antiderivatives of \(\tfrac{6}{x^{2}}\) are \(-\tfrac{6}{x}+{C}_{2}\), and the antiderivatives of \(\sin\) \(x\) are \(-\cos\) \(x + {C}_{3}\), the constant \(C\) in Example 2 is actually the sum of the constants \(C_{1},\) \(C_{2},\) and \(C_{3}.\)
An antiderivative of \(e^{x}\) is \(e^{x}.\) An antiderivative of \(6x^{-2}\) is \[ 6\cdot \frac{x^{-2+1}}{-2+1}=6\cdot \dfrac{x^{-1}}{-1}=-\dfrac{6}{x} \]
Finally, an antiderivative of \(\sin x\) is \(-\;\cos x\). Then all the antiderivatives of the function \(f\) are given by \[ F(x) =e^{x}-\frac{6}{x}+\cos x+C \]
where \(C\) is a constant.
NOW WORK
Problem 27.
2 Solve a Differential Equation
In studies of physical, chemical, biological, and other phenomena, scientists attempt to find mathematical laws that describe and predict observed behavior. These laws often involve the derivatives of an unknown function \(F\), which must be determined.
For example, suppose we seek all functions \(y = F(x)\) for which \[ \dfrac{dy}{dx}=F^\prime (x) = f(x)\]
An equation of the form \(\dfrac{dy}{dx}=f(x)\) is an example of a differential equation.* Any function \(y=F(x)\), for which \(\dfrac{dy}{dx}=f(x)\), is a solution of the differential equation. The general solution of a differential equation \(\dfrac{dy}{dx}=f(x)\) consists of all the antiderivatives of \(f\).
For example, the general solution of the differential equation \(\dfrac{dy}{dx}=5x^{2}+2\) is \[ \begin{eqnarray*} y={\frac{5}{3}}x^{3}+2x+C \end{eqnarray*} \]
In the differential equation \(\dfrac{dy}{dx}=5x^{2}+2\), suppose the solution must satisfy the boundary condition when \(x=3\), then \(y=5\). We use the general solution as follows: \[ \begin{eqnarray*} \begin{array}{rclc} y &=&{\dfrac{5}{3}}x^{3}+2x+C & \\[8pt] 5 &=&{{\dfrac{5}{3}}}(3^{3}) +2(3)+ C =45+6+C\qquad \color{#0066A7}{{x=3,\quad y=5}} \\[5pt] &&\qquad\qquad\qquad C =-46 \end{array} \end{eqnarray*} \]
332
The particular solution of the differential equation \(\dfrac{dy}{dx} =5x^{2}+2\) satisfying the boundary condition when \(x=3,\) then \(y=5\) is \[ y={\frac{5}{3}}x^{3}+2x-46 \]
*In Chapter 16, we give a more complete definition of a differential equation.

Solving a Differential Equation
Solve the differential equation \(\dfrac{dy}{dx}=x^{2}+2x+1\) with the boundary condition when \(x=3,\) then \(y={-}1.\)
Solution We begin by finding the general solution of the differential equation, namely \[ y=\frac{x^{3}}{3}+x^{2}+x+C \]
To determine the number \(C\), we use the boundary condition when \(x=3,\) then \(y={-}1\). \[ \begin{array}{rl@{\qquad}l} -1 &=\dfrac{3^{3}}{3}+3^{2}+3+C & \color{#0066A7}{{x=3,\quad y=-1}} \\[8pt] C&=-22 \end{array} \]
The particular solution of the differential equation with the boundary condition when \(x=3,\) then \(y=-1\), is \[ y=\frac{x^{3}}{3}+x^{2}+x-22 \]
NOW WORK
Problem 35.
Differential equations often involve higher-order derivatives. For example, the equation \(\dfrac{d^{2}y}{dx^{2}}=12x^{2}\) is an example of a second-order differential equation. The order of a differential equation is the order of the highest-order derivative of \(y\) appearing in the equation.
In solving higher-order differential equations, the number of arbitrary constants in the general solution equals the order of the differential equation. For particular solutions, a first-order differential equation requires one boundary condition; a second-order differential equation requires two boundary conditions; and so on.
Solving a Second-Order Differential Equation
Solve the differential equation \(\dfrac{d^{2}y}{dx^{2}}=12x^{2}\) with the boundary conditions when \(x=0,\) then \(y=1\) and when \(x=3,\) then \(y=8\).
Solution All the antiderivatives of \(\dfrac{d^{2}y}{dx^{2}}=12x^{2}\) are \[ \hspace{12pt}\dfrac{dy}{dx}=4x^{3}+C_{1} \]
All the antiderivatives of \(\dfrac{dy}{dx}=4x^{3}+C_{1}\) are \[ y=x^{4}+C_{1}x+C_{2} \]
This is the general solution of the differential equation. To find \(C_{1}\) and \(C_{2}\) and the particular solution to the differential equation, we use the boundary conditions.
- When \(x=0,\qquad 1=0^{4}+C_{1}( 0) +C_{2}\qquad \hbox{so}\quad C_{2}=1\)
- When \(x=3,\qquad 8=3^{4}+3C_{1}+1\qquad \hbox{so}\quad C_{1}=-\dfrac{74}{3}\)
333
The particular solution with the given boundary conditions is \[ y=x^{4}-\dfrac{74}{3}x+1 \]
NOW WORK
Problem 39.
3 Solve Applied Problems Modeled by Differential Equations
Rectilinear Motion
Suppose the functions \(s=s(t), v=v(t)\), and \(a=a(t)\) represent the distance \(s\), velocity \(v\), and acceleration \(a\), respectively, of an object at time \(t \). The three quantities \(s\), \(v\), and \(a\) are related by the differential equations \[ \dfrac{ds}{dt}=v(t) \qquad \hbox{ and }\qquad \dfrac{{d\kern-1ptv}}{dt}=a(t) \]
If the acceleration \(a=a(t)\) is a known function of the time \(t\), then the velocity can be found by solving the differential equation \(\dfrac{{d\kern-1ptv}}{dt} =a(t)\). Similarly, if the velocity \(v=v (t)\) is a known function of \(t\), then the distance \(s\) from the origin at time \(t\) is the solution of the differential equation \(\dfrac{ds}{dt}=v(t)\).
In physical problems, boundary conditions are often the values of the velocity \(v\) and distance \(s\) at time \(t=0\). In such cases, \(v(0)=v_{0}\) and \(s(0)=s_{0}\) are referred to as initial conditions.
Solving a Rectilinear Motion Problem
Find the distance \(s\) of an object from the origin at time \(t\) if its acceleration \(a\) is \[ a(t)=8t-3 \]
and the initial conditions are \(v_{0}=v(0)=4\) and \(s_{0}=s(0)=1.\)
Solution First we solve the differential equation \(\dfrac{{d\kern-1ptv}}{dt} =a(t)=8t-3\) and use the initial condition \(v_{0}=v( 0) =4\). \[ \begin{eqnarray*} v(t) &=& 4t^{2}-3t+C_{1} \\[3pt] {v_{0}} &=& v( 0) =4( 0) ^{2}-3( 0) + C_{1}&=&4 \\[0pt] &&\qquad\quad\hspace{3.9pc}C_{1}&=&4 \end{eqnarray*} \]
The velocity of the object at time \(t\) is \(v(t)=4t^{2}-3t+4\).
The distance \(s\) of the object at time \(t\) satisfies the differential equation \[ \frac{ds}{dt}=v(t)=4t^{2}-3t+4 \]
Then \[ {s(t)={\frac{4}{3}}t^{3}-{\frac{3}{2}}t^{2}+4t+C_{2}} \]
Using the initial condition, \(s_{0}=s(0)=1\), we have \[ \begin{eqnarray*} {s_{0}=s(0)=0-0+0+C_{2}} &=&1 \\ {C_{2}} &=&1 \end{eqnarray*} \]
The distance \(s\) of the object from the origin at any time \(t\) is \[ s=s(t) ={\frac{4}{3}}t^{3}-{\frac{3}{2}}t^{2}+4t+1 \]
NOW WORK
Problem 41.
334
Solving a Rectilinear Motion Problem
When the brakes of a car are applied, the car decelerates at a constant rate of \(10\;{\rm{m/s}}^2\). If the car is to stop within \(20 {\rm m}\) after the brakes are applied, what is the maximum velocity the car could have been traveling? Express the answer in miles per hour.
Solution Let \(s(t)\) represent the distance \(s\) in meters the car has traveled \(t\) seconds after the brakes are applied. Let \(v_{0}\) be the velocity of the car at the time the brakes are applied (\(t=0\)). Since the car decelerates at the rate of \(10\;{\rm{m/s}}^2\), its acceleration \(a,\) in meters per second squared, is \[ {a}(t) =\dfrac{{d\kern-1ptv}}{dt}={-10} \]
We solve the differential equation for \(v\). \[ v(t)=-10t+C_{1} \]
When \(t=0\), \(v(0)=v_{0}\), the velocity of the car when the brakes are applied, so \(C_{1}=v_{0}.\) Then \[ {v(t)={\frac{ds}{dt}}}={-10t+v_{0}} \]
Now we solve the differential equation \({v(t)={\dfrac{ds}{dt}}}\) for \(s\). \[ s(t)= -5t^{2}+v _{0}t+C_{2} \]
Since the distance \(s\) is measured from the point at which the brakes are applied, the second initial condition is \(s( 0) =0\). Then \(s( 0) =-5\cdot 0+v_{0}\cdot 0+C_{2}=0\), so \(C_{2}=0\). The distance \(s\), in meters, the car travels \(t\) seconds after applying the brakes is \[ s(t)=-5t^{2}+v_{0}t \]
The car stops completely when its velocity equals \(0\). That is, when \[ \begin{eqnarray*} v(t) ={-10t+v_{0}} &=&0 \\[3pt] t &=&{\frac{v_{0}}{10}} \end{eqnarray*} \]
This is the time it takes the car to come to rest. Substituting \(\dfrac{v_{0}}{10}\) for \(t\) in \(s(t)\), the distance the car has traveled is \[ s\left( {\frac{v_{0}}{10}}\right) =-5\left( {\frac{v_{0}}{10}}\right) ^{2}+v_{0}\left( {\frac{v_{0}}{10}}\right) =\frac{v_{0}^{2}}{20}\hbox{ } \]
If the car is to stop within 20 m, then \(s\leq 20\); that is, \(\dfrac{v_{0}^{2}}{20}\leq 20\) or equivalently \(v_{0}^{2}\le 400\). The maximum possible velocity \(v_{0}\) for the car is \(v_{0}=20 \ {\rm m}/{\rm s}\).
To express this in miles per hour, we proceed as follows: \[ \begin{eqnarray*} v_{0}=20\,{\rm{m}/{s}}&=&\left( \frac{20{{\rm m}}}{{{\rm s}}}\right)\, \left( \frac{1{\rm km}}{1000\,{{\rm m}}}\right)\, \left( \frac{3600 {{\rm s}} }{1\,{\rm h}}\right) \\[3pt] &=& 72{\rm km}/{\rm h}\approx \left( \frac{72\,{\rm km} }{{\rm h}}\right)\, \left( \frac{1\,{\rm mi}}{1.6\,{\rm km}}\right) =45 {\rm mi}/{\rm h} \end{eqnarray*} \]
The maximum possible velocity to stop within \(20\) m is \(45\) mi/h.
NOW WORK
Problem 53.
Freely Falling Objects
An object falling toward Earth is a common example of motion with (nearly) constant acceleration. In the absence of air resistance, all objects, regardless of size, weight, or composition, fall with the same acceleration when released from the same point above Earth’s surface, and if the distance fallen is not too great, the acceleration remains constant throughout the fall. This ideal motion, in which air resistance and the small change in acceleration with altitude are neglected, is called free fall. The constant acceleration of a freely falling object is called the acceleration due to gravity and is denoted by the symbol \(g\). Near Earth’s surface, its magnitude is approximately \(32\;{\rm ft}/{\rm s}^{2}\), or \(9.8\;{\rm m}/{\rm s}^{2}\), and its direction is down toward the center of Earth.
335
Solving a Problem Involving Free Fall
A rock is thrown straight up with an initial velocity of \(19.6\;{\rm m}/{\rm s}\) from the roof of a building \(24.5\;{\rm m}\) above ground level, as shown in Figure 65.
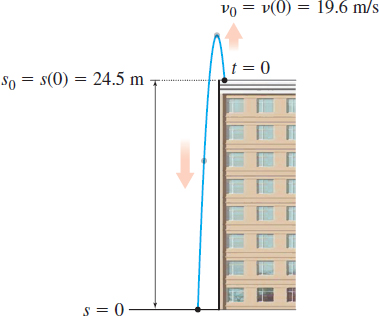
- How long does it take the rock to reach its maximum altitude?
- What is the maximum altitude of the rock?
- If the rock misses the edge of the building on the way down and eventually strikes the ground, what is the total time the rock is in the air?
Solution To answer the questions, we need to find the velocity \(v=v(t)\) and the distance \(s=s(t)\) of the rock as functions of time. We begin measuring time when the rock is released. If \(s\) is the distance, in meters, of the rock from the ground, then since the rock is released at a height of \(24.5\;{\rm m}\), \(s_{0}=s(0)=24.5\;{\rm m}\).
The initial velocity of the rock is given as \(v_{0}=v(0)=19.6\;{\rm m}/{\rm s}\). If air resistance is ignored, the only force acting on the rock is gravity. Since the acceleration due to gravity is \(-9.8\;{\rm m}/{\rm s}^{2}\), the acceleration \(a\) of the rock is \[ a=\dfrac{{d\kern-1ptv}}{dt}=-9.8 \]
Solving the differential equation, we get \[ v(t)=-9.8t+v_{0} \]
Using the initial condition, \(v_{0}=v( 0) =19.6\;{\rm m}/{\rm s}\), the velocity of the rock at any time \(t\) is \[ v(t)=-9.8t+19.6 \]
Now we solve the differential equation \(\dfrac{ds}{dt}=v(t) =-9.8t+19.6\). Then \[ {s}(t)={-4.9t^{2}+19.6t+s_{0}} \]
Using the initial condition, \(s( 0) =24.5\;{\rm m}\), the distance \(s\) of the rock from the ground at any time \(t\) is \[ s(t)=-4.9t^{2}+19.6t+24.5 \]
Now we can answer the questions.
- The rock reaches its maximum altitude when its velocity is \(0\). \begin{eqnarray*} v(t) &&= -9.8t+19.6=0 \\[6pt] t &&= 2 \end{eqnarray*} The rock reaches its maximum altitude at \(t=2\) seconds.
- To obtain the maximum altitude, we evaluate \(s(2)\). The maximum altitude of the rock is \[ s(2)=-4.9( 2^2) +19.6( 2) +24.5=44.1{\rm m} \]
- We find the total time the rock is in the air by solving \(s(t) =0\). \begin{eqnarray*} {\ -4.9t^{2}+19.6t+24.5} &&= 0 \\[1pt] {t^{2}-4t-5} &&= 0 \\[1pt] {(t-5)(t+1)} &&= 0 \\[1pt] t &&= 5\ \hbox{or}\quad t=-1 \end{eqnarray*}
336
The only meaningful solution is \(t=5\). The rock is in the air for \(5\) seconds.
Now we examine the general problem of freely falling objects.
If \(F\) is the weight of an object of mass \(m\), then according to Galileo, assuming air resistance is negligible, a freely falling object obeys the equation \[ F = -mg \]
where \(g\) is the acceleration due to gravity. The minus sign indicates that the object is falling. Also, according to Newton’s Second Law of Motion, \(F=ma\), so we have \[ {ma} = -{mg}\qquad \hbox{ or } \qquad a = {-g} \]
where \(a\) is the acceleration of the object. We seek formulas for the velocity \(v\) and distance \(s\) from Earth of a freely falling object at time \(t\).
Let \(t=0\) be the instant we begin to measure the motion of the object, and suppose at this instant the object’s vertical distance above Earth is \(s_{0}\) and its velocity is \(v_{0}.\) Since the acceleration \(a=\dfrac{{d\kern-1ptv}}{dt}\) and \(a = -g,\) we have \[\bbox[5px, border:1px solid black, #F9F7ED]{a=\dfrac{{d\kern-1ptv}}{{dt}}=-g} \tag{1} \]
Solving the differential equation (1) for \(v\) and using the initial condition \(v_{0}=v( 0)\), we obtain \[\bbox[5px, border:1px solid black, #F9F7ED]{v(t) =-gt+v_{0}} \]
Now since \(\dfrac{ds}{dt}=v(t)\), we have \[ \dfrac{ds}{dt}=-gt+v_{0} \tag{2} \]
Solving the differential equation (2) for \(s\) and using the initial condition \(s_{0}=s( 0) ,\) we obtain \[\bbox[5px, border:1px solid black, #F9F7ED]{s(t) ={-{\dfrac{1}{2}}}gt^{2}+v_{0}t+s_{0}} \]
NOW WORK
Problem 55.
Newton’s First Law of Motion
We close this section with a special case of the Law of Inertia, which was originally stated by Galileo.
THEOREM Newton’s First Law of Motion
If no force acts on a body, then a body at rest remains at rest and a body moving with constant velocity will continue to do so.
Proof
The force \(F\) acting on a body of mass \(m\) is given by Newton’s Second Law of Motion \(F=ma\), where \(a\) is the acceleration of the body. If there is no force acting on the body, then \(F=0\). In this case, the acceleration \(a\) must be \(0\). But \(a=\dfrac{{d\kern-1ptv}}{dt}\), where \(v\) is the velocity of the body. So, \[ {\dfrac{{d\kern-1ptv}}{dt}=0}\qquad \hbox{and}\qquad {v=}\hbox{ Constant} \]
337
That is, the body is at rest \((v=0)\) or else in a state of uniform motion (\(v\) is a nonzero constant).