Question

Related rates A spherical snowball is melting at the rate of \(2\) \({\rm{cm}}^3/\min\). How fast is the surface area changing when the radius is \(5\) cm?

Question

Related rates A lighthouse is \(3\, {\rm km}\) from a straight shoreline. Its light makes one revolution every \(8\) seconds. How fast is the light moving along the shore when it makes an angle of \(30^{ {\circ }}\) with the shoreline?

Question

Related rates Two planes at the same altitude are approaching an airport, one from the north and one from the west. The plane from the north is flying at \(250\, {\rm mph}\) and is \(30\) mi from the airport. The plane from the west is flying at \(200 \,{\rm mi}/{\rm h}\) and is \(20 \,{\rm mi}\) from the airport. How fast are the planes approaching each other at that instant?

Question

Question

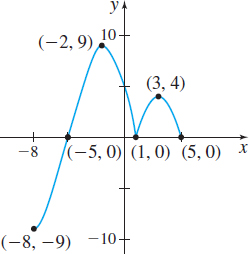
Question

Critical Numbers \(f(x)=\dfrac{ x^{2}}{2x-1}\)

1. Find all the critical numbers of \(f\).
2. Find the local extrema of \(f.\)

Question

Critical Numbers Find all the critical numbers of \(f(x)=\cos (2x) \) on the closed interval \([0,\pi ]\).

Question

\(f(x) =x-\!\sin (2x) \) on \([0,2\pi]\)

Question

\(f(x) =\) \(\dfrac{3}{2}x^{4}-2x^{3}-6x^{2}+5\) on \([-2, 3]\)

Question

Rolle’s Theorem Verify that the hypotheses for Rolle’s Theorem are satisfied for the function \(f(x)=x^{3}-4x^{2}+4x\) on \([0,2].\) Find the coordinates of the point(s) at which there is a horizontal tangent line to the graph of \(f\).

Question

Mean Value Theorem Verify that the hypotheses for the Mean Value Theorem are satisfied for the function \(f(x)=\dfrac{2x-1}{x}\) on the interval \([1,4].\) Find a point on the graph of \(f\) that has a tangent with a slope equal to that of the secant line joining \((1,1) \) to \( \left( 4,\dfrac{7}{4}\right).\)

Question

Mean Value Theorem Does the Mean Value Theorem apply to the function \(f(x)=\sqrt{x}\) on the interval \([0,9]\)? If not, why not? If so, find the number \(c\) referred to in the theorem.

Question

\(f(x)=x^{3}-x^{2}-8x+1\)

Question

\(f(x)=x^{2}-24x^{2/3}\)

Question

\(f(x)=x^{4}e^{-2x}\)

Question

Rectilinear Motion The distance \(s\) of an object from the origin at time \(t\) is given by \(s=s(t) =t^{4}+2t^{3}-36t^{2}\). Draw figures to illustrate the motion of the object and its velocity.

Question

\(f(x)=-x^{3}-x^{2}+2x\)

Question

\(f(x)=x^{1/3}(x^{2}-9)\)

Question

\(f(x)=xe^{x}\)

Question

\(f(x) =\dfrac{x-3}{x^{2}-4}\)

Question

\(f(x)=x\sqrt{x-3}\)

Question

\(f(x) =x^{3}-3\ln\;x\)

341

Question

\(f(x)=x^{4}+12x^{2}+36x-11\)

Question

\(f(x)=3x^{4}-2x^{3}-24x^{2}-7x+2\)

Question

If \(y\) is a function and \(y\prime >0\) for all \(x\) and \( y{\prime \prime} <0\) for all \(x\), which of the following could be part of the graph of \(y=f(x)\) ? See illustrations (A) through (D).

Question

Sketch the graph of a function \(f\) that has the following properties:

\(f(-3)=2;~f(-1)=-5;~f(2)=-4;\)

\(f(6)=-1~f'(-3) = f^\prime (6)=0\)

\(\lim\limits_{x\rightarrow 0^{-}}f(x)=-\infty;~\lim\limits_{x \rightarrow 0^{+}}f(x)=\infty;\)

\(f^{\prime \prime} (x)>0 \hbox{ if } x<-3 \hbox{ or } 0<x<4\)

\(f^{\prime\prime} (x)<0 \hbox{ if } -\!3<x<0 \hbox{ or } 4<x\)

Question

Sketch the graph of a function \(f\) that has the following properties:

\(f(-2)=2; f(5)=1; f(0)=0\)

\(f^\prime (x)>0 \hbox{ if } x<-2 \hbox{ or } 5<x\)

\(f^\prime (x)<0 \hbox{ if }\;-2<x<2 \hbox{or } 2<x<5\)

\(f^{\prime \prime} (x)>0 \hbox{ if } x<0 \hbox{ or } 2<x\;{\rm {and}}\;f^{\prime \prime} (x)<0 \hbox{ if } 0<x<2\)

\(\lim\limits_{x\rightarrow 2^{-}}f(x)=-\infty \lim\limits_{x\rightarrow 2^{+}}f(x)=\infty\)

Question

Mean Value Theorem For the function \(f(x)=x\sqrt{x+1},\) \(0\leq x\leq b\), the number \(c\) satisfying the Mean Value Theorem is \(c=3\). Find \(b\).

Question

Maximizing Volume An open box is to be made from a piece of cardboard by cutting squares out of each corner and folding up the sides. If the size of the cardboard is \(2 \,{\rm ft}\) by \(3 \,{\rm ft}\), what size squares (in inches) should be cut out to maximize the volume of the box?

Question

Minimizing Distance Find the point on the graph of \(2y=x^{2}\) nearest to the point \((4,1)\).

Question

\(f(x) =0\)

Question

\(f(x) =x^{1/2}\)

Question

\(f(x) =\cos x\)

Question

\(f(x) =\sec x\tan x\)

Question

\(f(x) =\dfrac{2}{x}\)

Question

\(f(x) =-2x^{-3}\)

Question

\(f(x)=4x^{3}-9x^{2}+10x-3\)

Question

\(f(x)=e^{x}+\dfrac{4}{x}\)

Question

Velocity A box moves down an inclined plane with an acceleration \(a(t) = \) \(t^{2}(t-3)\)\({\rm{cm/s}}^2 \). It covers a distance of \(10 \,{\rm cm}\) in \(2 \,{\rm seconds}\). What was the original velocity of the box?

Question

Free Fall Two objects begin a free fall from rest at the same height \(1\) second apart. How long after the first object begins to fall will the two objects be \(10 \,{\rm m}\) apart?

Question

\(\dfrac{xe^{3x}-x}{1-\cos (2x) }\)

Question

\(\left( \dfrac{1}{x}\right) ^{\tan x}\)

Question

\(\dfrac{1}{x^{2}}-\dfrac{1}{x^{2}\sec x}\)

Question

\(\dfrac{\tan x-x}{x-\!\sin x}\)

Question

\(\lim\limits_{x\rightarrow {\pi }/{2}}\dfrac{\sec ^{2}x}{\sec ^{2}(3x) }\)

Question

\(\lim\limits_{x\rightarrow 0}\left[ \dfrac{2}{\sin ^{2}x}-\dfrac{1}{1-\cos x}\right] \)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{e^{x}-e^{-x}}{\sin x} \)

Question

\(\lim\limits_{x\rightarrow 0^{-}}x\;\cot \left( \pi x\right) \)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\tan x+\sec x-1}{\tan x-\sec x+1}\)

Question

\(\lim\limits_{x\rightarrow a}\dfrac{ax-x^{2}}{a^{4}-2a^{3}x+2ax^{3}-x^{4}}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{x-\!\sin x}{x^{3}}\)

Question

\(\lim\limits_{x\rightarrow 0}\dfrac{\tan x-\!\sin x}{\sin ^{3}x}\)

Question

\(\lim\limits_{x\rightarrow \infty }(1+4x)^{2/x}\)

Question

\(\lim\limits_{x\rightarrow 1}\left[ \dfrac{2}{x^{2}-1}-\dfrac{1}{x-1}\right] \)

Question

\(\lim\limits_{x\rightarrow 4}\dfrac{x^{2}-16}{x^{2}+x-20}\)

Question

\(\lim\limits_{x\rightarrow 0^{+}}(\cot x)^{x}\)

Question

\(\dfrac{\textit{dy}}{\textit{dx}}=e^{x}\), when \(x=0\), \(y=2\)

Question

\(\dfrac{\textit{dy}}{\textit{dx}}=\dfrac{1}{2}\sec x\tan x,\) when \(x=0,\) \(y=7\)

Question

\(\dfrac{\textit{dy}}{\textit{dx}}=\dfrac{2}{x}\), when \(x=1,\) then \(y=4\)

Question

\(\dfrac{d^{2}y}{dx^{2}}=x^{2}-4,\) when \(x=3\), \(y=2,\) when \(x=2,\) \(y=2\)

Question

Maximizing Profit A manufacturer has determined that the cost \(C\) of producing \(x\) items is given by \(C(x) =200+35x+ 0.02x^{2}\) dollars. Each item can be sold for \({\$}78\). How many items should she produce to maximize profit?

Question

Optimization The sales of a new stereo system over a period of time are expected to follow the logistic curve \[ f(x)=\frac{5000}{1+5e^{-x}} \qquad x\geq 0 \]

where \(x\) is measured in years. In what year is the sales rate a maximum?

Question

Maximum Area Find the area of the rectangle of largest area in the fourth quadrant that has vertices at \((0,0)\), \((x,0)\), \(x>0\), and \((0,y)\), \(y<0\). The fourth vertex is on the graph of \(y=\ln x\).

Question

Differential Equation A motorcycle accelerates at a constant rate from \(0\) to \(72 \,{\rm km}/{\rm h}\) in 10 seconds. How far has it traveled in that time?