4.1 Related Rates
255
OBJECTIVES
When you finish this section, you should be able to:
- Solve related rate problems (p. 255)
In the natural sciences and in many of the social and behavioral sciences, there are quantities that are related to each other, but that vary with time. For example, the pressure of an ideal gas of fixed volume is proportional to the temperature, yet each of these variables may change over time. Problems involving the rates of change of related variables are called related rate problems. In a related rate problem, we seek the rate at which one of the variables is changing at a certain time, when the rates of change of the other variables are known.
1 Solve Related Rate Problems
We approach related rate problems by writing an equation involving the time-dependent variables. This equation is often obtained by investigating the geometric and/or physical conditions imposed by the problem. We then differentiate the equation with respect to time and obtain a new equation that involves the variables and their rates of change with respect to time.
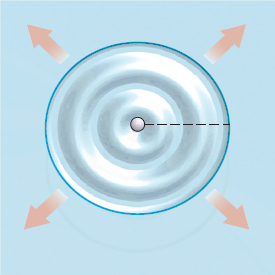
For example, suppose an object falling into still water causes a circular ripple, as illustrated in Figure 1. Both the radius and the area of the circle created by the ripple increase with time and their rates of growth are related. We use the formula for the area of a circle \[ A=\pi r^{2} \]
to relate the radius and the area. Both \(A\) and \(r\) are functions of time \(t\), and so the area of the circle can be expressed as \[ A(t) =\pi [r(t)] ^{2} \]
Now we differentiate both sides with respect to \(t\), obtaining \[ \dfrac{ \textit{dA}}{\textit{dt}}=2\pi r\dfrac{\textit{dr}}{\textit{dt}} \]
The derivatives (rates of change) are related by this equation, so we call them related rates. We can solve for one of these rates if the value of the other rate and the values of the variables are known.
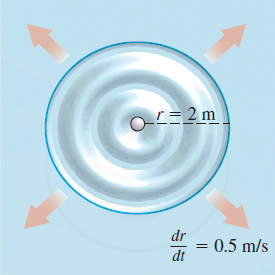
Solving a Related Rate Problem
A golfer hits a ball into a pond of still water, causing a circular ripple as shown in Figure 2. If the radius of the circle increases at the constant rate of \(0.5 \,{\rm m}/{\rm s}\), how fast is the area of the circle increasing when the radius of the ripple is \(2 \,{\rm m}\)?
Solution The quantities that are changing, that is, the variables of the problem, are \[ \begin{eqnarray*} t &=& \hbox{the time (in seconds) elapsed from the time when the ball hits the water} \\ r &=& \hbox{the radius (in meters) of the ripple after } t \hbox{ seconds} \\ A &=& \hbox{the area (in square meters) of the circle formed by the ripple after } t \hbox{ seconds} \end{eqnarray*} \]
The rates of change with respect to time are \[ \begin{eqnarray*} \dfrac{\textit{dr}}{\textit{dt}} &=& \hbox{the rate (in meters per second) at which the radius of the ripple is increasing} \\[5pt] \dfrac{\textit{dA}}{\textit{dt}} &=& \hbox{the rate (in meters squared per second) at which the area of the circle is}\\[-5pt] && \hbox{increasing} \end{eqnarray*} \]
It is given that \(\dfrac{\textit{dr}}{\textit{dt}}=0.5 \,{\rm m}/{\rm s}\). We seek \(\dfrac{\textit{dA}}{\textit{dt}}\) when \(r=2 \,{\rm m}\).
256
The relationship between \(A\) and \(r\) is given by the formula for the area of a circle: \[ A=\pi r^{2} \]
Since \(A\) and \(r\) are functions of \(t\), we differentiate with respect to \(t\) to obtain \[ \frac{\textit{dA}}{\textit{dt}}=2\pi r\frac{\textit{dr}}{\textit{dt}} \]
Since \(\dfrac{\textit{dr}}{\textit{dt}}=0.5 \,{\rm m}/{\rm s}\), \[ \dfrac{ \textit{dA}}{\textit{dt}}=2\pi r( 0.5) =\pi r \]
When \(r=2\)m, \[ \frac{\textit{dA}}{\textit{dt}}=\pi (2)=2 \pi \]
The area of the circle is increasing at a rate of about \(6.283~{\rm m}^{2}/{\rm s}\).
Steps for Solving a Related Rate Problem
Step 1 Read the problem carefully, perhaps several times. Pay particular attention to the rate you are asked to find. If possible, draw a picture to illustrate the problem.
Step 2 Identify the variables, assign symbols to them, and label the picture. Identify the rates of change as derivatives. Indicate what is given and what is asked for.
Step 3 Write an equation that relates the variables. It may be necessary to use more than one equation.
Step 4 Differentiate both sides of the equation(s).
Step 5 Substitute numerical values for the variables and the derivatives. Solve for the unknown rate.
CAUTION
Numerical values cannot be substituted (Step 5) until after the equation has been differentiated (Step 4).
NOW WORK
Problem 7.
Solving a Related Rate Problem
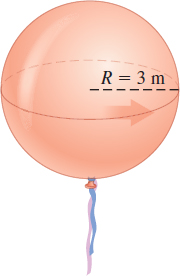
A spherical balloon is inflated at the rate of \(10~{\rm{m}}^3/{\rm min}\). Find the rate at which the surface area of the balloon is increasing when the radius of the sphere is \(3 \,{\rm m}\).
Solution We follow the steps for solving a related rate problem.
Step 1 Figure 3 shows a sketch of the balloon with its radius labeled.
Step 2 Identify the variables of the problem: \[ \begin{eqnarray*} t &=& \hbox{the time (in minutes) measured from the moment the balloon begins} \\[-3pt] && \hbox{inflating} \\ R &=& \hbox{the radius (in meters) of the balloon at time } t \\ V &=& \hbox{the volume (in meters cubed) of the balloon at time } t \\ S &=& \hbox{the surface area (in meters squared) of the balloon at time } t \end{eqnarray*} \]
Identify the rates of change: \[ \begin{eqnarray*} \dfrac{\textit{dR}}{\textit{dt}} &=& \hbox{the rate of change of the radius of the balloon (in meters per minute)} \\[6pt] \dfrac{\textit{dV}}{\textit{dt}} &=& \hbox{the rate of change of the volume of the balloon (in meters cubed per}\\[-5pt] && \hbox{minute)} \\[6pt] \dfrac{\textit{dS}}{\textit{dt}} &=& \hbox{the rate of change of the surface area of the balloon (in meters squared}\\[-5pt] && \hbox{per minute)} \end{eqnarray*} \]
We are given \(\dfrac{\textit{dV}}{\textit{dt}}=10~{\rm{m}}^3 /{\rm min} \), and we seek \(\dfrac{\textit{dS}}{\textit{dt}}\) when \(R=3 \,{\rm m}\).
257
NEED TO REVIEW?
Geometry formulas\(\!\!\!\!\!\!\!\!\) are discussed in Appendix A.2, p. A-15.
Step 3 Since both the volume \(V\) of the balloon (a sphere) and its surface area \(S\) can be expressed in terms of the radius \(R,\) we use two equations to relate the variables. \[ V=\frac{4}{3}\pi\! R^{3}\quad\hbox{ and }\quad S=4\pi\! R^{2} \qquad \hbox{ where } V, S,\hbox{ and }R\hbox{ are functions of }t \]
Step 4 Differentiate both sides of the equations with respect to time \(t.\) \[ \frac{\textit{dV}}{\textit{dt}}=4\pi\! R^{2} \,\frac{\textit{dR}}{\textit{dt}}\qquad \hbox{ and }\qquad \frac{ \textit{dS}}{ \textit{dt}}=8 \pi\! R \,\frac{\textit{dR}}{\textit{dt}} \]
Combine the equations by solving for \(\dfrac{\textit{dR}}{\textit{dt}}\) in the equation on the left and substituting the result into the equation for \(\dfrac{\textit{dS}}{\textit{dt}}\) on the right. Then \[ \frac{ \textit{dS}}{ \textit{dt}}=8\pi\! R\!\left(\!\dfrac{\dfrac{\textit{dV}}{\textit{dt}}}{{4\pi\! R^{2}}}\!\right) = \frac{2}{R}\frac{\textit{dV}}{\textit{dt}} \]
Step 5 Substitute \(R=3 \,{\rm m}\) and \(\dfrac{\textit{dV}}{\textit{dt}}=10 \,{\rm{m}}^3 /{\rm min} \). \[ \frac{ \textit{dS}}{ \textit{dt}}=\left( \frac{2}{3}\right) (10)\approx 6.667 \]
When the radius of the balloon is \(3 \,{\rm m}\), its surface area is increasing at the rate of about \(6.667 \,{\rm{m}}^2/{\rm min} \).
NOW WORK
Problems 11 and 17.

Solving a Related Rate Problem
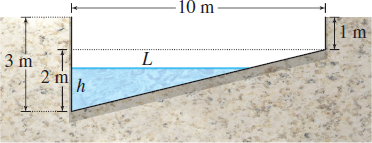
A rectangular swimming pool \(10 \, {\rm m}\) long and \(5 \,{\rm m}\) wide has a depth of \(3 \,{\rm m}\) at one end and \(1 \,{\rm m}\) at the other end. If water is pumped into the pool at the rate of \(300\) liters per minute (\({\rm liter}/{\rm min}\)), at what rate is the water level rising when it is \(1.5 \,{\rm m}\) deep at the deep end?
Solution
Step 1 We draw a picture of the cross-sectional view of the pool, as shown in Figure 4.
Step 2 The width of the pool is \(5 \,{\rm m}\), the water level (measured at the deep end) is \(h\), the distance from the wall at the deep end to the edge of the water is \(L\), and the volume of water in the pool is \(V\). Each of the variables \(h\), \(L\), and \(V\) varies with respect to time \(t\). \[ {\rm We\;are\;given} \dfrac{\textit{dV}}{\textit{dt}}=300\, {\rm liter}/ {\rm min}\; {\rm and\;are\;asked\;to\;find} \dfrac{\textit{dh}}{\textit{dt}} {\rm when}\; h=1.5\; {\rm m}. \]
NEED TO REVIEW?
Similar triangles are discussed in Appendix A.2, pp. A-13 to A-14.
Step 3 The volume \(V\) is related to \(L\) and \(h\) by the formula \[ V=\hbox{(Cross-sectional triangular area)(width)}=\left( \dfrac{1}{2} Lh\right) (5) =\dfrac{5}{2}Lh \]
See Figure 4. Using similar triangles, \(L\) and \(h\) are related by the equation \[ \frac{L}{h}=\frac{10}{2} \qquad\hbox{so} \qquad L=5h \]
Now we can write \(V\) as \[ \begin{eqnarray*} V = \frac{5}{2} \textit{Lh} \underset{\underset{{\color{#0066A7}{\hbox{L=5h}}}}{\color{#0066A7}{\uparrow }}} {=} \frac{5}{2}(5h) h=\dfrac{25}{2}h^{2} \nonumber\\[-8.1pt]\tag{1} \end{eqnarray*} \]
Both \(V\) and \(h\) vary with time \(t\).
258
Step 4 We differentiate both sides of equation (1) with respect to \(t.\) \[ \dfrac{\textit{dV}}{\textit{dt}}=25h\,\frac{\textit{dh}}{\textit{dt}} \]
NOTE
\[ 1000\,{\rm liter} = 1\, {\rm m}^3 . \]
Step 5 Substitute \(h=1.5\) m and \(\dfrac{\textit{dV}}{\textit{dt}}=300\ {\rm liter}/{\rm min}= \dfrac{300}{1000}{\rm m}^{3\!\!}/{\rm min}=0.3{\rm m}^{3\!\!}/{\rm min}\). Then \[ \begin{eqnarray*} 0.3 &=&25(1.5) \dfrac{\textit{dh}}{\textit{dt}}\qquad\qquad \color{#0066A7}{{\hbox{\(\dfrac{dV}{dt}=25 h\dfrac{dh}{dt}\)}}} \\[3pt] \frac{\textit{dh}}{\textit{dt}} &=&\frac{0.3}{25(1.5)}=0.008 \end{eqnarray*} \]
When the height of the water is \(1.5\, {\rm m}\), the water level is rising at a rate of \(0.008\, {\rm m}/{\rm min}\).
NOW WORK
Problem 23.
Solving a Related Rate Problem
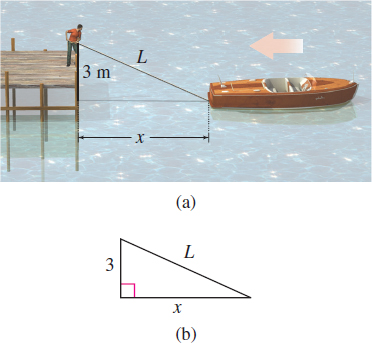
A person standing at the end of a pier is docking a boat by pulling a rope at the rate of \(2 \,{\rm m}/{\rm s}\). The end of the rope is \(3 \,{\rm m}\) above water level. See Figure 5(a). How fast is the boat approaching the base of the pier when \(5 \,{\rm m}\) of rope are left to pull in? (Assume the rope never sags, and that the rope is attached to the boat at water level.)
Solution
Step 1 Draw illustrations, like Figure 5, representing the problem. Label the sides of the triangle \(3\) and \(x\), and label the hypotenuse of the triangle \(L.\)
Step 2 \(x\) is the distance (in meters) from the boat to the base of the pier, \(L\) is the length of the rope (in meters), and the distance between the water level and the person's hand is \(3 \, {\rm m}\). Both \(x\) and \(L\) are changing with respect to time, so \(\dfrac{\textit{dx}}{\textit{dt}}\) is the rate at which the boat approaches the pier, and \(\dfrac{\textit{dL}}{ \textit{dt}}\) is the rate at which the rope is pulled in.
We are given \(\dfrac{\textit{dL}}{ \textit{dt}}=2 \,{\rm m}/{\rm s}\), and we seek \(\dfrac{\textit{dx}}{\textit{dt}}\) when \(L=5 \,{\rm m}\).
NEED TO REVIEW?
The Pythagorean Theorem is discussed in Appendix A.2, p. A-11.
Step 3 The lengths \(3\), \(x\), and \(L\) are the sides of a right triangle and, by the Pythagorean Theorem, are related by the equation \begin{equation*} x^{2}+3^{2}=L^{2}\tag{2} \end{equation*}
Step 4 We differentiate both sides of equation (2) with respect to \(t.\) \[ \begin{eqnarray*} 2x\frac{\textit{dx}}{\textit{dt}} &=&2L\frac{\textit{dL}}{\textit{dt}} \\[3pt] \frac{\textit{dx}}{\textit{dt}} &=&\dfrac{L}{x}\frac{\textit{dL}}{\textit{dt}}\qquad \color{#0066A7}{{\hbox{ Solve for }\tfrac{\textit{dx}}{\textit{dt}}.}} \end{eqnarray*} \]
Step 5 When \(L=5\), we use equation (2) to find \(x=4\). Since \(\dfrac{\textit{dL}}{\textit{dt}}=2\), \[ \begin{eqnarray*} \frac{\textit{dx}}{\textit{dt}} &=&\dfrac{5}{4}(2) \qquad \color{#0066A7}{{\hbox{\({L=5},{x=4}, \tfrac{\textit{dL}}{\textit{dt}} =2\)}}} \\[3pt] \frac{\textit{dx}}{\textit{dt}} &=&2.5 \end{eqnarray*} \]
When \(5 \,{\rm m}\) of rope are left to be pulled in, the boat is approaching the pier at the rate of \(2.5 \,{\rm m}/{\rm s}\).
NOW WORK
Problem 29.
259
Solving a Related Rate Problem
RECALL
For motion that is circular, angular speed \(\omega\) is defined as the rate of change of a central angle \(\theta\) of the circle with respect to time. That is, \(\omega = \dfrac{d \theta}{dt}\), where \(\theta\) is measured in radians.
A revolving light, located 5 \( {\rm km}\) from a straight shoreline, turns at constant angular speed of 3 \( {\rm rad}/\! {\rm min}\). With what speed is the spot of light moving along the shore when the beam makes an angle of \(60^\circ\) with the shoreline?
Solution Figure 6 illustrates the triangle that describes the problem. \[ \begin{eqnarray*} x &=& \hbox{the distance (in kilometers) of the beam of light from the point}\ B \\ \theta &=& \hbox{the angle (in radians) the beam of light makes with } AB \end{eqnarray*} \]
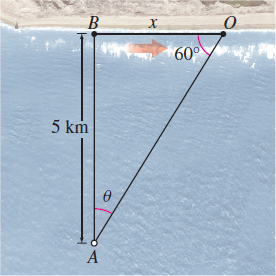
Both variables \(x\) and \(\theta\) change with time \(t\) (in minutes). The rates of change are \[ \begin{eqnarray*} \dfrac{\textit{dx}}{\textit{dt}} &=& \hbox{the speed of the spot of light along the shore (in kilometers per minute)} \\[4pt] \dfrac{d\theta }{\textit {dt}} &=& \hbox{the angular speed of the beam of light (in radians per minute)} \end{eqnarray*} \]
We are given \(\dfrac{d\theta }{dt}=3 \,{\rm rad}/{\rm min}\) and we seek \( \dfrac{\textit{dx}}{\textit{dt}}\) when the angle \(\textit{AOB}=60{{}^{\circ}} \).
From Figure 6, \[ \tan \theta =\frac{x}{5}\qquad\hbox{ so }x=5\tan \theta \]
Then \[ \frac{\textit{dx}}{\textit{dt}}=5\sec ^{2}\!\theta \frac{d\theta }{dt} \]
When \(\textit{AOB}=60 {{}^{\circ}} ,\) angle \(\theta =30 {{}^{\circ}} =\dfrac{\pi }{6}{\rm rad}\), and \[ \frac{\textit{dx}}{\textit{dt}}=\frac{5}{\cos ^{2}\theta }\frac{d\theta }{dt}=\frac{5(3)}{\left( {\cos \,}\dfrac{{\pi }}{6}\right) ^{2}}=\frac{15}{\dfrac{3}{4}}=20 \text{ } \]
When \(\theta =30 {{}^\circ} \), the light is moving along the shore at a speed of \(20 \,{\rm km}/{\rm min}\).
NOW WORK
Problem 37.