4.1 Assess Your UnderstandingPrinted Page 259
Concepts and Vocabulary
If a spherical balloon of volume \(V\) is inflated at a rate of \( 10\, {\rm m}^{3\!\!}/{\rm min},\) where \(t\) is the time (in minutes), what is the rate of change of \(V\) with respect to \(t\)?
\(10\ {\rm m}^3/{\rm min}\)
For the balloon in Problem 1, if the radius \(r\) is increasing at the rate of \(0.5\, {\rm m}/{\rm min}\), what is the rate of change of \(r\) with respect to \(t\)?
0.5 m/min
In Problems 3 and 4, \(x\) and \(y\) are differentiable functions of \(t\). Find \(\dfrac{\textit{dx}}{\textit{dt}}\) when \(x=3\), \(y=4\), and \(\dfrac{\textit{dy}}{\textit{dt}}=2\).
\(x^{2}+y^{2}=25\)
\(-\dfrac{8}{3}\)
\(x^{3}y^{2}=432\)
\(-1\)
Skill Building
Suppose \(h\) is a differentiable function of \(t\) and suppose that \(\dfrac{\textit{dh}}{\textit{dt}}=\dfrac{5}{16}\pi \) when \(h=8\). Find \(\dfrac{\textit{dV}}{\textit{dt}}\) when \(h=8\) if \(V=\dfrac{1}{12}\pi h^{3}\).
\(5\pi ^2\)
Suppose \(x\) and \(y\) are differentiable functions of \(t\) and suppose that when \(t=20\), \(\dfrac{\textit{dx}}{\textit{dt}}=5\), \(\dfrac{\textit{dy}}{\textit{dt}}=4\), \(x=150\), and \(y=80\). Find \(\dfrac{\textit{ds}}{\textit{dt}}\) when \(t=20\) if \(s^{2}=x^{2}+y^{2}\).
Suppose \(h\) is a differentiable function of \(t\) and suppose that when \(h=3\), \(\dfrac{\textit{dh}}{\textit{dt}}=\dfrac{1}{12}\). Find \(\dfrac{\textit{dV}}{\textit{dt}} \) when \(h=3\) if \(V=80h^{2}\).
40
Suppose \(x\) is a differentiable function of \(t\) and suppose that when \(x=15\), \(\dfrac{\textit{dx}}{\textit{dt}}=3\). Find \(\dfrac{\textit{dy}}{\textit{dt}}\) when \(x=15\) if \( y^{2}=625-x^{2}, y\ge 0\).
Volume of a Cube If each edge of a cube is increasing at the constant rate of \(3\, {\rm cm}/{\rm s}\), how fast is the volume of the cube increasing when the length \(x\) of an edge is \(10\, {\rm cm}\) long?
900 \({\rm cm}^3/{\rm s}\)
Volume of a Sphere If the radius of a sphere is increasing at \(1\, {\rm cm}/{\rm s}\), find the rate of change of its volume when the radius is \(6\, {\rm cm}\).
260
Radius of a Sphere If the surface area of a sphere is shrinking at the constant rate of \(0.1\, {\rm{cm}}^2 /{\rm h} \), find the rate of change of its radius when the radius is \(\dfrac{20}{\pi} {\rm cm}\).
\(-0.000625\) cm/h
Surface Area of a Sphere If the radius of a sphere is increasing at the constant rate of \(2\, {\rm cm}/{\rm min}\), find the rate of change of its surface area when the radius is \(100 {\rm cm}\).
Dimensions of a Triangle Consider a right triangle with hypotenuse of (fixed) length \(45\, {\rm cm}\) and variable legs of lengths \(x\) and \(y\), respectively. If the leg of length \(x\) increases at the rate of \(2\, {\rm cm}/{\rm min}\), at what rate is \(y\) changing when \(x=\) \(4 \,{\rm cm}\)?
\(-\dfrac{8}{\sqrt{2009}} \approx -0.178\) cm/min
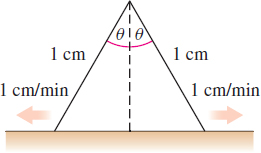
Change in Area The fixed sides of an isosceles triangle are of length 1cm. (See the figure.) If the sides slide outward at a speed of \(1 \,{\rm cm}/{\rm min}\), at what rate is the area enclosed by the triangle changing when \(\theta =30^{\circ}\)?
Area of a Triangle An isosceles triangle has equal sides \(4 \,{\rm cm}\) long and the included angle is \(\theta \). If \( \theta \) increases at the rate of \(2 { {{}^\circ}}/ {\rm min}\), at what rate is the area of the triangle changing when \(\theta \) is \(30 {{}^\circ}\)?
\(\dfrac{2\sqrt{3} \pi}{45} \approx 0.242\ {\rm cm}^2/{\rm min}\)
Area of a Rectangle In a rectangle with a diagonal \(15\)cm long, one side is increasing at the rate of \(2\sqrt{5} \, {\rm cm}\) /s. Find the rate of change of the area when that side is \(10 \,{\rm cm}\) long.
Change in Surface Area A spherical balloon filled with gas has a leak that causes the gas to escape at a rate of \(1.5 \,{\rm{m}}^3 /\min .\) At what rate is the surface area of the balloon shrinking when the radius is \(4 \,{\rm m}\)?
\(-0.75\ {\rm m}^2/{\rm min}\)
Frozen Snow Ball Suppose that the volume of a spherical ball of ice decreases (by melting) at a rate proportional to its surface area. Show that its radius decreases at a constant rate.
Applications and Extensions
Change in Inclination A ladder \(5 \,{\rm m}\) long is leaning against a wall. If the lower end of the ladder slides away from the wall at the rate of \(0.5 \,{\rm m}/{\rm s}\), at what rate is the inclination \(\theta \) of the ladder with respect to the ground changing when the lower end is \(4 \,{\rm m}\) from the wall?
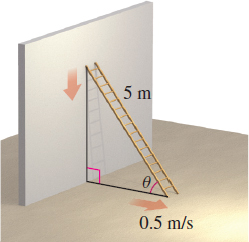
\(-\dfrac{1}{6}\) rad/s
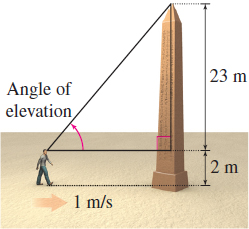
Angle of Elevation A man \(2 \,{\rm m}\) tall walks horizontally at a constant rate of \(1 \,{\rm m}/{\rm s}\) toward the base of a tower \(25 \,{\rm m}\) tall. When the man is \(10 \,{\rm m}\) from the tower, at what rate is the angle of elevation changing if that angle \({\rm is\; measured}\) from the horizontal to the line joining the top of the man's head to the top of the tower?
Filling a Pool A public swimming pool is \(30 \,{\rm m}\) long and \(5 \,{\rm m}\) wide. Its depth is \(3 \,{\rm m}\) at the deep end and \(1 \,{\rm m}\) at the shallow end. If water is pumped into the pool at the rate of \(15 \,{\rm{m}}^3 /{\rm min}\), how fast is the water level rising when it is \(1 \,{\rm m}\) deep at the deep end? Use Figure 4 as a guide.
0.2 m/min
Filling a Tank Water is flowing into a vertical cylindrical tank of diameter \(6 \,{\rm m}\) at the rate of \(5\ \,{\rm{m}}^3 /{\rm min}\). Find the rate at which the depth of the water is rising.
Fill Rate A container in the form of a right circular cone (vertex down) has radius \(4 \,{\rm m}\) and height \(16 {\rm m}\). See the figure. If water is poured into the container at the constant rate of \(16 \,{\rm{m}}^3 /\min\), how fast is the water level rising when the water is \(8 \,{\rm m}\) deep? ( Hint: The volume \(V\) of a cone of radius \(r\) and height \(h\) is \(V=\dfrac{1}{3}\pi r^{2}h\).)
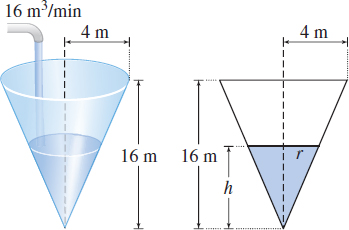
\( \dfrac{4}{\pi} \approx 1.273\) m/min
Building a Sand Pile Sand is being poured onto the ground, forming a conical pile whose height equals one-fourth of the diameter of the base. If the sand is falling at the rate of \(20 \,{\rm{cm}}^3 /{\rm s}\), how fast is the height of the sand pile increasing when it is \(3 \,{\rm cm}\) high?
Is There a Leak? A cistern in the shape of a cone \(4 \,{\rm m} \) deep and \(2 \,{\rm m}\) in diameter at the top is being filled with water at a constant rate of \(3 \,{\rm{m}}^3 /{\rm min}\).
- (a) At what rate is the water rising when the water in the tank is \(3 \,{\rm m}\) deep?
- (b) If, when the water is \(3 \,{\rm m}\) deep, it is observed that the water rises at a rate of \(0.5 \,{\rm m}/{\rm min}\), at what rate is water leaking from the tank?
- (a) \(\dfrac{16}{3 \pi}\approx 1.698\) m/min
- (b) \(\dfrac{96-9\pi}{32} \approx 2.116 \ {\rm m}^3/{\rm min}\)
Change in Area The vertices of a rectangle are at \((0, 0)\), \( (0, e^{x})\), \((x, 0)\), and \((x, e^{x}), x>0\). If \(x\) increases at the rate of \(1\) unit per second, at what rate is the area increasing when \(x=10\) units?
Distance from the Origin An object is moving along the parabola \(y^{2}=4(3-x)\). When the object is at the point \(\left( -1,4\right) \), its \(y\)-coordinate is increasing at the rate of \(3\) units per second. How fast is the distance from the object to the origin changing at that instant?
\(\dfrac{18}{\sqrt{17}} \approx 4.366\) units/s
Funneling Liquid A conical funnel \(15 \,{\rm cm}\) in diameter and \(15 \,{\rm cm}\) deep is filled with a liquid that runs out at the rate of \( 5 \,{\rm{cm}}^3 /{\rm min}\). At what rate is the depth of liquid changing when its depth is \(8 \,{\rm cm}\)?
Baseball A baseball is hit along the third-base line with a speed of \(100 \,{\rm ft}/{\rm s}\). At what rate is the ball's distance from first base changing when it crosses third base? See the figure.

\(50\sqrt{2}\) ft/s
261
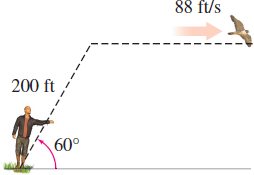
Flight of a Falcon A peregrine falcon flies up from its trainer at an angle of \(60{{}^\circ}\) until it has flown \(200 \,{\rm ft}\). It then levels off and continues to fly away. If the constant speed of the bird is \(88 \,{\rm ft}/{\rm s}\), how fast is the falcon moving away from the falconer after it is \(6 \,{\rm seconds}\) in flight. See the figure.
Source: http://www.rspb.org.uk.
Boyle’s Law A gas is said to be compressed adiabatically if there is no gain or loss of heat. When such a gas is diatomic (has two atoms per molecule), it satisfies the equation \(PV^{1.4}=k\), where \(k\) is a constant, \(P\) is the pressure, and \(V\) is the volume. At a given instant, the pressure is \(20 \,{\rm{kg}}/{\rm cm}^2\), the volume is \(32 \,{\rm cm}^{3}\) , and the volume is decreasing at the rate of \(2 \,{\rm cm}^{3\!\!}/{\rm min}\). At what rate is the pressure changing?
\(1.75 \ {\rm kg}/{\rm cm}^2/{\rm min}\)
Heating a Plate When a metal plate is heated, it expands. If the shape of the plate is circular and its radius is increasing at the rate of \(0.02 \,{\rm cm}/{\rm s}\), at what rate is the area of the top surface increasing when the radius is \(3 \,{\rm cm}\)?
Pollution After a rupture, oil begins to escape from an underwater well. If, as the oil rises, it forms a circular slick whose radius increases at a rate of \(0.42 \,{\rm ft}/{\rm min}\), find the rate at which the area of the spill is increasing when the radius is \(120 \,{\rm ft}\).
\(100.8\pi \approx 316.673\ {\rm ft}^2/{\rm min}\)
Flying a Kite A girl flies a kite at a height \(30 \,{\rm m}\) above her hand. If the kite flies horizontally away from the girl at the rate of \(2 \,{\rm m}/{\rm s}\), at what rate is the string being let out when the length of the string released is \(70 \,{\rm m}\)? Assume that the string remains taut.
Falling Ladder An \(8\)-\({\rm m}\) ladder is leaning against a vertical wall. If a person pulls the base of the ladder away from the wall at the rate of \(0.5 \,{\rm m}/{\rm s}\), how fast is the top of the ladder moving down the wall when the base of the ladder is
- (a) \(3 \,{\rm m}\) from the wall?
- (b) \(4 \,{\rm m}\) from the wall?
- (c) \(6 \,{\rm m}\) from the wall?
- (a) \(\dfrac{1.5}{\sqrt{55}} \approx 0.202\) m/s
- (b) \(\dfrac{0.5}{\sqrt{3}} \approx 0.289\) m/s
- (c) \(\dfrac{1.5}{\sqrt{7}} \approx 0.567\) m/s
Beam from a Lighthouse A light in a lighthouse \(2000 \,{\rm m}\) from a straight shoreline is rotating at \(2\) revolutions per minute. How fast is the beam moving along the shore when it passes a point \(500 \,{\rm m}\) from the point on the shore opposite the lighthouse? ( Hint: One revolution \(=2\pi \,{\rm rad}\).)
Moving Radar Beam A radar antenna, making one revolution every \(5\, \,{\rm seconds}\), is located on a ship that is \(6 \,{\rm km}\) from a straight shoreline. How fast is the radar beam moving along the shoreline when the beam makes an angle of \(45^{\circ}\) with the shore?
\(\dfrac{24\pi}5 \approx 15.08\) km/s
Tracking a Rocket When a rocket is launched, it is tracked by a tracking dish on the ground located a distance \(D\) from the point of launch. The dish points toward the rocket and adjusts its angle of elevation \(\theta \) to the horizontal (ground level) as the rocket rises. Suppose a rocket rises vertically at a constant speed of \(2.0 \,{\rm m}/{\rm s}\), with the tracking dish located \(150 \,{\rm m}\) from the launch point. Find the rate of change of the angle \(\theta \) of elevation of the tracking dish with respect to time \(t\) (tracking rate) for each of the following:
- (a) Just after launch.
- (b) When the rocket is \(100 \,{\rm m}\) above the ground.
- (c) When the rocket is \(1.0 \, {\rm km}\) above the ground.
- (d) Use the results in (a)-(c) to describe the behavior of the tracking rate as the rocket climbs higher and higher. What limit does the tracking rate approach as the rocket gets extremely high?
Lengthening Shadow A child, \(1 \,{\rm m}\) tall, is walking directly under a street lamp that is \(6 \,{\rm m}\) above the ground. If the child walks away from the light at the rate of \(20 \,{\rm m}/{\rm min}\), how fast is the child’s shadow lengthening?
4 m/min
Approaching a Pole A boy is walking toward the base of a pole \(20 \,{\rm m}\) high at the rate of \(4 \,{\rm km}/{\rm h}\). At what rate (in meters per second) is the distance from his feet to the top of the pole changing when he is \(5 \,{\rm m}\) from the pole?
Riding a Ferris Wheel A Ferris wheel is \(50\, {\rm ft}\) in diameter and its center is located \(30 \,{\rm ft}\) above the ground. See the image. If the wheel rotates once every \(2\,{\rm min}\), how fast is a passenger rising when he is \(42.5 \,{\rm ft}\) above the ground? How fast is he moving horizontally?

He is rising at \(\dfrac{25\sqrt3 \pi}2 \approx 68.017\) ft/min. He is moving horizontally at \(\dfrac{-25\pi}2 \approx -32.270\) ft/min.
Approaching Cars Two cars approach an intersection, one heading east at the rate of \(30 \,{\rm km}/{\rm h}\) and the other heading south at the rate of \(40 \,{\rm km}/{\rm h}\). At what rate are the two cars approaching each other at the instant when the first car is \(100 \,{\rm m}\) from the intersection and the second car is \(75 \,{\rm m}\) from the intersection? Assume the cars maintain their respective speeds.
Parting Ways An elevator in a building is located on the fifth floor, which is \(25 \,{\rm m}\) above the ground. A delivery truck is positioned directly beneath the elevator at street level. If, simultaneously, the elevator goes down at a speed of \(5 \,{\rm m}/{\rm s}\) and the truck pulls away at a speed of \(8 \,{\rm m}/{\rm s}\), how fast will the elevator and the truck be separating 1 second later? Assume the speeds remain constant at all times.
\(-\dfrac{9\sqrt{29}}{29}\approx\! -1.671\) m/s
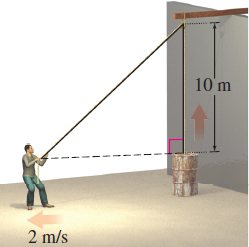
Pulley In order to lift a container \(10 \,{\rm m}\), a rope is attached to the container and, with the help of a pulley, the container is hoisted. See the figure. If a person holds the end of the rope and walks away from beneath the pulley at the rate of \(2\, {\rm m}/{\rm s}\), how fast is the container rising when the person is \(5 \,{\rm m}\) away? Assume the end of the rope in the person’s hand was originally at the same height as the top of the container.
Business A manufacturer of precision digital switches has daily cost \(C\) and revenue \(R\) functions, in dollars, of \(C(x)\kern1pt {=}\,10{,}000\,{+}\,3x\) and \(R(x) =5x-\dfrac{x^{2}}{2000}\), respectively, where \(x\) is the daily production of switches. Production is increasing at the rate of \(50\) switches per day when production is \(1000\) switches.
262
- (a) Find the rate of increase in cost when production is \(1000\) switches per day.
- (b) Find the rate of increase in revenue when production is \(1000\) switches per day.
- (c) Find the rate of increase in profit when production is \(1000\) switches per day. ( Hint: \(\hbox{Profit} = \hbox{Revenue} - \hbox{Cost}\))
- (a) $150/day
- (b) $200/day
- (c) $50/day
An Enormous Growing Black Hole In December 2011 astronomers announced the discovery of the two most massive black holes identified to date. The holes appear to be quasar* remnants, each having a mass equal to \(10\) billion Suns. Huge black holes typically grow by swallowing nearby matter, including whole stars. In this way, the size of the event horizon (the distance from the center of the black hole to the position at which no light can escape) increases. From general relativity, the radius \(R\) of the event horizon for a black hole of mass \(m\) is \(R=\dfrac{2Gm}{c^{2}}\), where \(G\) is the gravitational constant and \(c\) is the speed of light in a vacuum.
*A quasar is an astronomical object that emits massive amounts of electromagnetic radiation.
- (a) If one of these huge black holes swallows one Sun-like star per year, at what rate (in kilometers per year) will its event horizon grow? The mass of the Sun is \(1.99\times 10^{30}\,{\rm kg}\), the speed of light in a vacuum is \(c=3.00\times 10^{8}{\rm m}/{\rm s}\), and \(G=6.67\times 10^{-11}{\rm m} ^{3\!\!}/({\rm kg}\cdot {\rm s}^{2}) \).
- (b) By what percent does the event horizon change per year?
Weight in Space An object that weighs \(K\) \({\rm lb}\) on the surface of Earth weighs approximately \[ W(R)=K\!\left( \frac{3960}{3960+R}\right) ^{\!\!2} \]
pounds when it is a distance of \(R\) \({\rm mi}\) from Earth’s surface. Find the rate at which the weight of an object weighing \(1000 \,{\rm lb}\) on Earth’s surface is changing when it is \(50 \,{\rm mi}\) above Earth’s surface and is being lifted at the rate of \(10\, {\rm mi}/{\rm s}\).
\(\approx\! -4.864\) lb/s
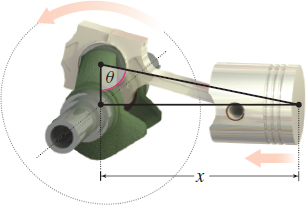
Pistons In a certain piston engine, the distance \(x\) in meters between the center of the crank shaft and the head of the piston is given by \(x=\cos \theta + \sqrt{16-\!\sin^{2}\theta }\), where \(\theta \) is the angle between the crank and the path of the piston head. See the figure below.
- (a) If \(\theta \) increases at the constant rate of \(45 \,{\rm radians}/{\rm second}\), what is the speed of the piston head when \(\theta =\dfrac{\pi }{6}\)?
- (b)
 Graph \(x\) as a function of \(\theta \) on the interval \( [0,\pi] \). Determine the maximum distance and the minimum distance of the piston head from the center of the crank shaft.
Graph \(x\) as a function of \(\theta \) on the interval \( [0,\pi] \). Determine the maximum distance and the minimum distance of the piston head from the center of the crank shaft.
Tracking an Airplane A soldier at an anti-aircraft battery observes an airplane flying toward him at an altitude of \(4500 \,{\rm ft}\). See the figure. When the angle of elevation of the battery is \(30 {{}^\circ}\), the soldier must increase the angle of elevation by \(1{{}^\circ}/{\rm second}\) to keep the plane in sight. What is the ground speed of the plane?

\(-100 \pi \approx -314.159\) ft/s
Change in the Angle of Elevation A hot air balloon is rising at a speed of \(100 \,{\rm m}/{\rm min}\). If an observer is standing \(200 \,{\rm m}\) from the lift-off point, what is the rate of change of the angle of elevation of the observer’s line of sight when the balloon is \(600 \,{\rm m}\) high?
Rate of Rotation A searchlight is following a plane flying at an altitude of \(3000 \,{\rm ft}\) in a straight line over the light; the plane’s velocity is \(500 \,{\rm mi}/{\rm h}\). At what rate is the searchlight turning when the distance between the light and the plane is \(5000 \,{\rm ft}\)? See the figure.

\(-316.8\) rad/h
Police Chase A police car approaching an intersection at \(80 \,{\rm ft}/{\rm s}\) spots a suspicious vehicle on the cross street. When the police car is \(210 \,{\rm ft}\) from the intersection, the policeman turns the spotlight on the vehicle, which is at that time just crossing the intersection at a constant rate of \(60 \,{\rm ft}/{\rm s}\). See the figure. How fast must the light beam be turning \(2 \,{\rm s}\) later in order to follow the suspicious vehicle?

Change in Volume The height \(h\) and width \(x\) of an open box with a square base are related to its volume by the formula \(V=hx^{2}\). Discuss how the volume changes
- (a) if \(h\) decreases with time, but \(x\) remains constant.
- (b) if both \(h\) and \(x\) change with time.
- (a) Answers will vary.
- (b) Answers will vary.
Rate of Change Let \(y=2e^{\cos x}\). If both \(x\) and \(y\) vary with time in such a way that \(y\) increases at a steady rate of 5 units per second, at what rate is \(x\) changing when \(x=\dfrac{\pi }{2}\)?
Challenge Problems
Moving Shadows The dome of an observatory is a hemisphere \(60\, {\rm ft}\) in diameter. A boy is playing near the observatory at sunset. He throws a ball upward so that its shadow climbs to the highest point on the dome. How fast is the shadow moving along the dome \(\dfrac{1}{2}\) second after the ball begins to fall? How did you use the fact that it was sunset in solving the problem? ( Note: A ball falling from rest covers a distance \(s\,{=} \,16t^{2} \,{\rm ft}\) in \(t\) seconds.)
263
\(\approx 32.071\) ft/s
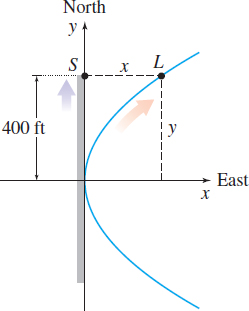
Moving Shadows A railroad train is moving at a speed of \(15 \,{\rm mi}/{\rm h}\) past a station \(800 \,{\rm ft}\) long. The track has the shape of the parabola \(y^{2}=600x\) as shown in the figure. If the sun is just rising in the east, find how fast the shadow \(S\) of the locomotive \(L\) is moving along the wall at the instant it reaches the end of the wall.
Change in Area The hands of a clock are \(2 \,{\rm in}\) and \(3\, {\rm in}\) long. See the figure. As the hands move around the clock, they sweep out the triangle OAB. At what rate is the area of the triangle changing at 12:10 p.m.?

\(\approx 0.165 \ {\rm in}^2/{\rm min}\)
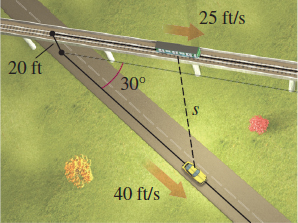
Distance A train is traveling northeast at a rate of \(25 \,{\rm ft}/{\rm s}\) along a track that is elevated \(20 \,{\rm ft}\) above the ground. The track passes over the street below at an angle of \(30{{}^\circ} \). See the figure. Five seconds after the train passes over the road, a car traveling east passes under the tracks going \(40 \,{\rm ft}/{\rm s}\). How fast are the train and the car separating after \(3\) seconds?