OBJECTIVES

When you finish this section, you should be able to:

1. Find an indefinite integral using substitution (p. 387)
2. Find a definite integral using substitution (p. 391)
3. Integrate even and odd functions (p. 393)
4. Solve differential equations: Newton's Law of Cooling (p. 394)

NEED TO REVIEW?

Differentials are discussed in Section 3.4, pp. 230-232.

NOTE

When using the method of substitution, once the substitution \(u\) is chosen, we write the original integral in terms of \(u\) and \(du\).

NEED TO REVIEW?

The Chain Rule is discussed in Section 3.1, pp. 198-200.

Finding Indefinite Integrals Using Substitution

Find:

1. \(\int \sin (3x+2)\,dx \)
2. \(\int x\sqrt{x^{2}+1}\,dx\)
3. \(\int \dfrac{e^{\sqrt{{ x}}}}{\sqrt{x}}dx\)

Solution (a) Since we know \(\int \sin x\,dx,\) we let \(u = 3x + 2\). Then \(du = 3\,dx\) so \(dx = \dfrac{du}{3}\). \[ \begin{eqnarray*} \int \sin (\underset{\color{#0066A7}{\hbox{\(u\)}}}{\underbrace{(3x+2)}}\enspace\underset{\color{#0066A7}{\tfrac{du}{2}}}{\underbrace{dx}}&=& \int {\sin }\,u\dfrac{du}{3}=\dfrac{1}{3}\int {\sin }\,u\,du\\ &=&\dfrac{1}{3}({-}\cos u)+C \underset{\underset{{\color{#0066A7}{\hbox{\(u=3 x+2\)}}}}{\color{#0066A7}{\uparrow }}}{=} -\dfrac{1}{3}{\cos }(3x+2)+C \end{eqnarray*} \]

(b) We let \(u = x^{2} + 1\). Then \(du = 2x\,dx\), so \(x\,dx = \dfrac{du}{2}\). \[ \begin{eqnarray*} \int x\sqrt{x^{2}+1}\,dx &=& \int \underset{\color{#0066A7}{\hbox{\(u\)}}}{{\underbrace{\sqrt{x^{2}+1}}}\,}\underset{\color{#0066A7}{\hbox{\(\tfrac{du}{2}\)}}}{\underbrace{x\,dx}}=\int \sqrt{u}\,\dfrac{du}{2}=\dfrac{1}{2}\int u^{1/2}du=\dfrac{1}{2}\left(\dfrac{u^{3/2}}{\dfrac{3}{2}}\right) +C \\ &= & \dfrac{(x^{2}+1) ^{3/2}}{3} +C \end{eqnarray*} \]

(c) We let \(u=\sqrt{x}=x^{1/2}\). Then \(du=\dfrac{1}{2}x^{-1/2}dx=\dfrac{dx}{2\sqrt{x}}\), so \(\dfrac{dx}{\sqrt{x}}\) \(=2du\). \[ \int \dfrac{e^{\sqrt{{ x}}}}{\sqrt{x}}dx=\int e^{\sqrt{x}}\cdot \dfrac{dx}{\sqrt{x}}=\int e^{u}\cdot 2du=2e^{u}+C=2e^{\sqrt{{ x}}}+C \]

NOW WORK

Problems 5 and 11.

Finding Indefinite Integrals Using Substitution

Find:

1. \(\int \dfrac{5x^{2}dx}{4x^{3}-1}\)
2. \( \int \dfrac{e^{x}}{e^{x}+4}dx\)

Solution (a) Notice that the numerator equals the derivative of the denominator, except for a constant factor. So, we try substitution. Let \(\ u=4x^{3}-1.\) Then \(du=12x^{2}dx\) so \(5x^{2}dx=\dfrac{5}{12}\,du\). \[ \int \dfrac{5x^{2}dx}{4x^{3}-1}=\int \dfrac{\dfrac{5}{12}\,du}{u}=\dfrac{5}{12}\int \dfrac{du}{u}=\dfrac{5}{12}\ln \left\vert u\right\vert +C=\dfrac{5}{12}\ln \left\vert 4x^{3}-1\right\vert +C \]

(b) Here, the numerator equals the derivative of the denominator. So, we use the substitution \(u=e^{x}+4\). Then \(du=e^{x}dx\). \[ \begin{eqnarray*} \int \dfrac{e^{x}}{e^{x}+4}dx=\int \dfrac{1}{e^{x}+4}\cdot e^{x}dx=\int \dfrac{1}{u}\,du=\ln \vert u\vert +C \underset{\underset{{\color{#0066A7}{\hbox{\(u=e^{x}+4>0\)}}}}{\color{#0066A7}{\uparrow}}}{=} \ln (e^{x}+4) +C \\ \end{eqnarray*} \]

NOW WORK

Problem 17.

Using Substitution To Establish an Integration Formula

Show that:

1. \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int \tan x\,dx=-\ln \left\vert \cos x\right\vert +C=\ln \vert \sec x\vert +C }} \]
2. \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int \sec x\,dx=\ln \vert \sec x+\tan x\vert +C }} \]

Solution (a) Since \(\tan x=\dfrac{\sin x}{\cos x},\) we let \(u=\cos x.\) Then \(du=-\sin x\, dx\) and \[ \begin{eqnarray*} \int \tan x dx = \int \dfrac{\sin x}{\cos x}dx=\int -\dfrac{du}{u}=-\ln \left\vert u\right\vert +C=-\ln \left\vert \cos x\right\vert +C \\ \underset{ \underset{ \color{#0066A7}{\hbox{\(r\ln x=\ln x^{r}\)}} } {\color{#0066A7}{\uparrow}} } {=} \ln \left\vert \cos x\right\vert^{-1}+C =\ln \left\vert \dfrac{1}{\cos x}\right\vert + C =\ln \left\vert \sec x\right\vert +C \end{eqnarray*} \]

(b) To find \(\int \sec x dx\), we multiply the integrand by \(\dfrac{\sec x+\tan x}{\sec x+\tan x}.\) \[ \int \sec x dx=\int \sec x\cdot \dfrac{\sec x+\tan x}{\sec x+\tan x} dx=\int \dfrac{\sec ^{2}x+\sec x\tan x}{\sec x+\tan x} dx \]

Now the numerator equals the derivative of the denominator. So if \(u=\sec x+\tan x,\) then \(du=( \sec x\tan x+\sec ^{2}x) dx.\) \[ \int \sec x dx=\int \dfrac{du}{u}=\ln \left\vert u\right\vert +C=\ln \left\vert \sec x+\tan x\right\vert +C \]

NOW WORK

Problem 27.

IN WORDS

If the numerator of the integrand equals the derivative of the denominator, then the integral equals a logarithmic function.

Finding an Indefinite Integral Using Substitution

Find \(\int {x\sqrt{4+x}}\,dx\).

Solution Substitution I  Let \(u = 4 + x\). Then \(du = dx.\) Since \(u=4+x,\) \(x=u-4.\) Substituting gives \[ \begin{eqnarray*} \int {x\sqrt{4+x}}\,dx \underset{\underset{{\color{#0066A7}{\hbox{\(u=x+4\)}}}}{\color{#0066A7}{\uparrow }}} =&& \int \underset{\color{#0066A7}{\hbox{\(x\)}}}{\underbrace{( u-4) }} \underset{\underset{{\color{#0066A7}{\hbox{\(4+x\)}}}}{\color{#0066A7}{\uparrow }}}{{\sqrt{u}}}\,\,\underset{\color{#0066A7}{\hbox{\(dx\)}}}{\underbrace{du}}\, =\int {({u^{3/2}-4u^{1/2}})}\,du \\ &=& {\dfrac{{u^{5/2}}}{{{\dfrac{{5}}{{2}}}}}}-4\cdot {\dfrac{{u^{3/2}}}{{{\dfrac{{3}}{{2}}} }}}+C \\ &=&{\dfrac{{2({4+x})^{5/2}}}{{5}}}-{\dfrac{{8({4+x})^{3/2}}}{{3}}}+C \end{eqnarray*} \]

Substitution II  Let \(u = \sqrt{4\,{+}\,x}\), so \(u^{2} = 4 + x\) and \(x = u^{2} - 4\). Then \(dx=2u\,du\) and \[ \begin{eqnarray*} \int {x\sqrt{4+x}}\,dx & = &\int {(}\underset{\color{#0066A7}{\hbox{\(x\)}}}{\underbrace{{u^{2}-4}}}{)(u)(}\underset{\color{#0066A7}{\hbox{\(dx\)}}}{\underbrace{{2u\,du}}}{)= 2 \int {(u^{4}-4u^{2})\,du}}=2\left[ {\dfrac{{u^{5}}}{{5}}}-{\dfrac{{4u^{3}}}{{3}}}\right] +C \\ &=&\dfrac{2}{5} \big(\sqrt{4+x}\,\big) ^{5} -\dfrac{8}{3} \big(\sqrt{4+x}\,\big) ^{3}+C= \dfrac{2(4+x)^{5/2}}{5} -\dfrac{8(4+x)^{3/2}}{3}+C   \end{eqnarray*} \]

NOW WORK

Problem 35.

Finding Indefinite Integrals Using Substitution

Find:

1. \(\int \dfrac{dx}{\sqrt{4-x^{2}}}\)
2. \(\int \dfrac{dx}{9+4x^{2}}\)

Solution (a) \(\int \dfrac{dx}{\sqrt{4-x^{2}}}\) resembles \(\int \dfrac{1}{\sqrt{1-x^{2}}}\,dx=\) \(\sin ^{-1}x+C.\) We begin by rewriting the integrand as \[ \dfrac{1}{\sqrt{4-x^{2}}}=\dfrac{1}{\sqrt{4\left( 1-\dfrac{x^{2}}{4}\right) }}=\dfrac{1}{2\sqrt{1-\left( \dfrac{x}{2}\right) ^{2}}} \]

Now we let \(u=\dfrac{x}{2}\). Then \(du=\dfrac{dx}{2}\), so \(dx=2\,du.\) \[ \begin{eqnarray*} \int \dfrac{dx}{\sqrt{4-x^{2}}}&=&\int \dfrac{dx}{2\sqrt{1-\left( \dfrac{x}{2}\right) ^{2}}} \underset{\underset{{\underset{{\color{#0066A7}{\hbox{\(dx=2du\)}}}}{\color{#0066A7}{\hbox{\(u=\tfrac{x}{2}\)}}}}}{\color{#0066A7}{\uparrow}}} = \int \dfrac{2 du}{2\sqrt{1-u^{2}}}=\int \dfrac{du}{\sqrt{1-u^{2}}}=\sin ^{-1}u+C \\ &=&\sin ^{-1}\left( \dfrac{x}{2}\right) +C \end{eqnarray*} \]

(b) \(\int \dfrac{dx}{9+4x^{2}}\) resembles \(\int \dfrac{1}{1+x^{2}}dx=\tan ^{-1}x+C\). We rewrite the integrand as \[ \dfrac{1}{9+4x^{2}}=\dfrac{1}{9\left( 1+\dfrac{4x^{2}}{9}\right) }=\dfrac{1}{9\left[ 1+\left( \dfrac{2x}{3}\right) ^{2}\right] } \]

Now let \(u=\dfrac{2x}{3}.\) Then \(du=\dfrac{2}{3}dx\), so \(dx=\dfrac{3}{2} du\). \[ \begin{eqnarray*} \int \dfrac{dx}{9+4x^{2}}&=&\int \dfrac{dx}{9\left[ 1+\left( \dfrac{2x}{3} \right) ^{2}\right] }=\int \dfrac{\dfrac{3}{2}du}{9( 1+u^{2}) }=\dfrac{1}{6}\int \dfrac{du}{1+u^{2}} \\ &=& \dfrac{1}{6}\tan ^{-1}u+C=\dfrac{1}{6}\tan ^{-1}\left( \dfrac{2x}{3}\right) +C \end{eqnarray*} \]

NOW WORK

Problem 39.

• Method 1: Find the related indefinite integral using substitution, and then use the Fundamental Theorem of Calculus.
• Method 2: Find the definite integral directly by making a substitution in the integrand and using the substitution to change the limits of integration.

Finding a Definite Integral Using Substitution

Find \(\int_{0}^{2}x\sqrt{4-x^{2}}\,dx\).

Solution

Method 1: Use the related indefinite integral and then apply the Fundamental Theorem of Calculus. The related indefinite integral \(\int {x\sqrt{4-x^{2}}\,dx}\) can be found using the substitution \(u = 4 - x^{2}\). Then \(du\,=-2x\,dx\), so \(x\,dx=-\dfrac{du}{2}.\) \[ \begin{eqnarray*} \int {x\sqrt{4-x^{2}}\,dx}&=&\int {\sqrt{u}\left( {-}{\dfrac{{du}}{{2}}}\right) }={-}{\dfrac{{1}}{{2}}}\int u^{1/2}du=-\dfrac{1}{2}\cdot {{\dfrac{{u^{3/2}}}{{{ \dfrac{{3}}{{2}}}}}}}+C \\ &=&-\dfrac{1}{3}{{(4-x^{2})^{3/2}}}+C \end{eqnarray*} \]

Then by the Fundamental Theorem of Calculus, \[ \int_{0}^{2} x\sqrt{4-x^{2}}\,dx = -\dfrac{1}{3} \Big[(4-x^{2})^{3/2}\Big]_{0}^{2} = -\dfrac{1}{3}\big[0-4^{3/2}\big] =\dfrac{8}{3} \]

Method 2: Find the definite integral directly by making a substitution in the integrand and changing the limits of integration. We let \(u=4-x^{2}\); then \(du=-2x\,dx.\) Now use the function \(u=4-x^{2}\) to change the limits of integration.

• The lower limit of integration is \(x=0\) so, in terms of \(u,\) it becomes \(u=4-0^{2}=4\).
• The upper limit of integration is \(x=2\) so the upper limit becomes \(u=4-2^{2}=0\).

Then

\[ \begin{eqnarray*} {\int_{0}^{2}{x\sqrt{4-x^{2}}\,dx}} && \underset{\underset{{\underset{{\color{#0066A7}{\hbox{\(x dx=-\tfrac{1}{2}du\)}}}}{{\color{#0066A7}{\hbox{\(u=4-x^{2} \)}}}}}}{\color{#0066A7}{\uparrow }}}{=} \int_{4}^{0}\sqrt{u}\left( -\dfrac{du}{2}\right) =-\dfrac{1}{2}\int_{4}^{0} \sqrt{u} du=-\dfrac{1}{2}\cdot \left[ \dfrac{u^{3/2}}{\dfrac{3}{2}}\right] _{4}^{0} \\ {\;\;} &&= -{\dfrac{1}{3}}(0-8)={\dfrac{{8}}{{3}}} \end{eqnarray*} \]

NOW WORK

Problem 45.

Finding a Definite Integral Using Substitution

Find \(\int_{0}^{\pi /2}\dfrac{{1-\cos}(2\theta)}{2}\,d\theta \).

Solution We use properties of integrals to simplify before integrating. \[ \begin{eqnarray*} \int_{0}^{\pi /2}\dfrac{1-\cos (2\theta ) }{2}\,d\theta &=&\dfrac{1}{2}\int_{0}^{\pi /2}\left[ 1-\cos (2\theta ) \right] \,d\theta \\ &=& \dfrac{1}{2}\left[ \int_{0}^{\pi /2}d\theta -\int_{0}^{\pi /2}\cos (2\theta ) \,d\theta \right]\\ & =& \dfrac{1}{2}\int_{0}^{\pi /2}d\theta -\dfrac{1}{2}\int_{0}^{\pi /2}\cos (2\theta ) \,d\theta \\ &=& \dfrac{1}{2} \Big[\theta\Big] _{0}^{\pi /2}-\dfrac{1}{2}\int_{0}^{\pi /2}\cos (2\theta ) \,d\theta \\ &=& \dfrac{\pi }{4}-\dfrac{1}{2}\int_{0}^{\pi /2}\cos (2\theta ) \,d\theta \end{eqnarray*} \]

In the integral on the right, we use the substitution \(u = 2\theta \). Then \(du = 2\,d\theta \) so \(d\theta =\dfrac{du}{2}\). Now we change the limits of integration:

• when \( \theta = 0,\)   then \( u=2(0) =0 \)
• when \( \theta =\dfrac{\pi }{2},\)   then \( u=2\left( \dfrac{\pi }{2}\right) =\pi \)

Now \[ \int_{0}^{\pi /2}\cos (2\theta ) \,d\theta =\int_{0}^{\pi }{\cos u\,\dfrac{{du}}{{2}}}= \dfrac{1}{2}\Big[\sin u\Big] _{0}^{\pi }=\dfrac{1}{2}\left( \sin \pi -\sin 0\right) =0 \]

Then, \[ \int_{0}^{\pi /2}\dfrac{1-\cos (2\theta ) }{2}d\theta =\dfrac{\pi}{4}-\dfrac{1}{2}\int_{0}^{\pi /2}{\cos }(2\theta ) {\,d\theta }=\dfrac{\pi }{4} \]

NOW WORK

Problem 53.

NEED TO REVIEW?

Even and odd functions are discussed in Section P.1, pp. 9-10.

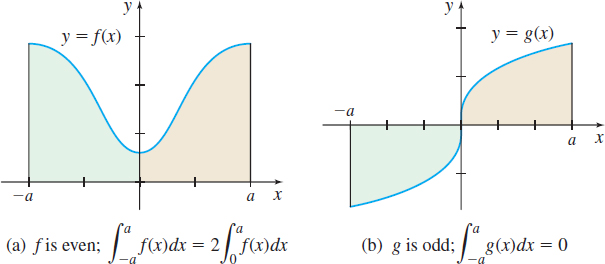
THEOREM The Integrals of Even and Odd Functions

Let a function \(f\) be continuous on a closed interval \([-a,a]\), \(a>\,0 \).

• If \(f\) is an even function, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt]{ \int_{-a}^{a}f(x)\,dx=2\int_{{0}}^{a}f(x)\,dx }} \]
• If \(f\) is an odd function, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt]{ \int_{-a}^{a} f(x)\,dx=0 }} \]

Proof

\(f\) is an even function:  Since \(f\) is continuous on the closed interval \([ -a,\,a] ,\) \(a>0,\) and \(0\) is in the interval \(\left[ -a,a\right] \), we have \[ \begin{equation*} \int_{-a}^{a} f(x)\,dx=\int_{-a}^{0} f(x)\,dx+ \int_{0}^{a}f(x)\,dx=-\int_{0}^{-a}f(x)\,dx+\int_{0}^{a}f(x)\,dx \tag {2} \end{equation*} \]

In \(- {\int_{0}^{-a}{f(x)\,dx}}\), we use the substitution \(u = -x\). Then \(du = -dx\). Also, if \(x=0\), then \(u=0\), and if \(x=-a\), then \(u = a\). Therefore, \[ \begin{eqnarray*} -{\int_{0}^{-a}{f(x)\,dx={\int_{0}^{a}{f({-}u)\,du}}}} \underset{\underset{{\underset{{\color{#0066A7}{\hbox{\(f(-u) =f(u) \)}}}}{\color{#0066A7}{\hbox{\(f\) is even}}}}}{\color{#0066A7}{\uparrow }}}= \int_{0}^{a}f(u) du=\int_{0}^{a}f(x)\, dx \tag{3} \end{eqnarray*} \]

Combining (2) and (3), we obtain \[ {\int_{{-}a}^{a}{f(x)\,dx={\int_{0}^{a}{f(x)\,dx}}}}+{\int_{0}^{a}{f(x)\,dx}}=2{\int_{0}^{a}{f(x)\,dx}} \]

Integrating an Even or Odd Function

Find:

1. \(\int_{-3}^{3}{(x^{7}-4x^{3}+x)}\,dx\)
2. \(\int_{-2}^{2}(x^{4}-x^{2}+3)\, dx\)

Solution (a) If \(f(x)={{x^{7}-4x^{3}+x,}}\) then \(f({-}x)=({-}x)^{7}-4({-}x)^{3}+({-}x)={-}(x^{7}-4x^{3}+x)={-}f(x).\) Since \(f\) is an odd function, \[ \int_{-3}^{3}{(x^{7}-4x^{3}+x)}\,dx=0 \]

(b) If \(g(x) =x^{4}-x^{2}+3,\) then \(g(-x) =(-x) ^{4}-(-x) ^{2}+3=x^{4}-x^{2}+3=g(x).\) Since \(g\) is an even function, \[ \begin{eqnarray*} \int_{-2}^{2}( x^{4}-x^{2}+3) dx &=& 2\int_{0}^{2}(x^{4}-x^{2}+3)\, dx=2\left[ \dfrac{x^{5}}{5}-\dfrac{x^{3}}{3}+3x\right]_{0}^{2} \\ &=& 2\left[ \dfrac{32}{5}-\dfrac{8}{3}+6\right] =\dfrac{292}{15} \end{eqnarray*} \]

NOW WORK

Problems 63 and 67.

Using Properties of Integrals

If \(f\) is an even function and \(\int_{0}^{2}f(x)\, dx=-6\) and \(\int_{-5}^{0}f(x)\, dx=8,\) find \(\int_{2}^{5}f(x)\, dx.\)

Solution \(\int_{2}^{5}f(x)\, dx=\int_{2}^{0}f(x)\, dx+\int_{0}^{5}f(x)\, dx\)

Now \(\int_{2}^{0}f(x)\, dx=-\int_{0}^{2}f(x)\, dx=6.\)

Since \(f\) is even, \(\int_{0}^{5}f(x)\, dx=\) \(\int_{-5}^{0}f(x)\, dx \) \(\,=8.\) Then \[ \int_{2}^{5}f(x)\, dx=\int_{2}^{0}f(x)\, dx+\int_{0}^{5}f(x)\, dx=6+8=14 \]

Using Newton's Law of Cooling

An object is heated to \(90{}^{\circ}{\rm C}\) and allowed to cool in a room with a constant ambient temperature of \(20{}^{\circ}{\rm C}\). If after \(10\) min the temperature of the object is \(60{}^{\circ}{\rm C}\), what will its temperature be after \(20\) min?

Solution When \(t=0\), \(u(0) =u_{0}=90{}^{\circ}{\rm C}\), and when \(t=10\) min, \(u\left( 10\right) =60{}^{\circ}{\rm C}\). Given that the ambient temperature \(T\) is \(20{}^{\circ}{\rm C}\), we substitute these values into equation (5). \[ \begin{eqnarray*} \begin{array}{rcl@{\qquad}l@{\hspace*{-6pc}}} u(t) &=&( u_{0}-T) e^{kt}+T \\ 60 &=&( 90-20) e^{10k}+20 & {\color{#0066A7}{\hbox{\(u=60 \hbox{ when }t=10; \ T=20;\ u_{0} =90\)}}} \\ \dfrac{40}{70} &=&e^{10k} \\ k &=&\dfrac{1}{10}\ln \dfrac{4}{7} = 0.1 0 \ln \dfrac{4}{7} \end{array} \end{eqnarray*} \]

The temperature \(u\) is \[ u(t) =70 e^{[0.1 \ln (4/7)]t} +20 \]

Then when \(t=20\), the temperature \(u\) of the object is \[ u (20) =70e ^{[0.1 \ln (4/7)] (20)} +20=70e^{2\ln (4/7)}+20\approx 42.86{}^{\circ}{\rm C} \]

NOW WORK

Problem 109.