5.2 Assess Your Understanding
Concepts and Vocabulary
Question
If an interval \([a,b]\) is partitioned into \(n\) subintervals \([x_{0},\,x_{1}],\) \([x_{1},\,x_{2}],\) \([x_{2},\,x_{3}],\) \(\ldots, \) \([x_{n-1},\,x_{n}]\), where \(a=x_{0}\lt x_{1}\lt x_{2}\lt\cdots \lt x_{n-1}\lt x_{n}=b,\) then the set of subintervals of the interval \([a,b]\) is called a(n) ________ of \([a,b]\).
Question
Multiple Choice In a regular partition of \([0,40] \) into \(20\) subintervals, \( \Delta x= \) [(a) 20 (b) 40 (c) 2 (d) 4].
Question
True or False A function \(f\) defined on the closed interval \([a,b] \) has an infinite number of Riemann sums.
Question
In the notation for a definite integral \(\int_{a}^{b}f(x)\, dx\), \(a\) is called the _______ _______; \(b\) is called the _______ _______; \(\int \) is called the _________ _________; and \(f(x) \) is called the_________.
Question
If \(f(a) \) is defined, \(\int_{a}^{a}f(x)\, dx=\) _________.
Question
True or False If a function \(f\) is integrable over a closed interval \([a,b] \), then \(\int_{a}^{b}f(x) dx=\int_{b}^{a}f(x) dx\).
Question
True or False If a function \(f\) is continuous on a closed interval \([a,b] \), then the definite integral \(\int_{a}^{b}f(x)\, dx\) exists.
Question
Multiple Choice Since \(\int_{0}^{2}(3x-8) dx=-10\), then \(\int_{2}^{0}(3x-8)\, dx=\) [(a) \(-\)2 (b) 10 (c) 5 (d) 0].
Skill Building
In Problems 9–12, find the Riemann sum for each function \(f\) for the partition and the numbers \(u_{i}\) listed.
Question
\({f(x)=x}\), \(0\leq x \leq 2\). Partition the interval \([0,2]\) as follows: \[ \begin{eqnarray*} &&x_{0}=0, x_{1}=\dfrac{1}{4}, x_{2}=\dfrac{1}{2}, x_{3}=\dfrac{3}{4}, x_{4}=1, x_{5}=2;\\ &&\left[0,\dfrac{1}{4}\right], \left[\dfrac{1}{4},\dfrac{1}{2}\right], \left[\dfrac{1}{2},\dfrac{3}{4}\right], \left[\dfrac{3}{4},1\right], [1,2] \end{eqnarray*} \]
and choose \[ u_{1}=\dfrac{1}{8}, u_{2}=\dfrac{3}{8}, u_{3}=\dfrac{5}{8}, u_{4}=\dfrac{7}{8}, u_{5}=\dfrac{9}{8}. \]
Question
\({f(x)=x}\), \(0\leq x \leq 2\). Partition the interval \([0,2]\) as follows: \(\left[0,\dfrac{1}{2}\right]\), \(\left[\dfrac{1}{2},1\right]\), \(\left[1,\dfrac{3}{2}\right]\), \(\left[\dfrac{3}{2},2\right]\), and choose \(u_{1}=\dfrac{1}{2}\), \(u_{2}=1\), \(u_{3}=\dfrac{3}{2}\), \(u_{4}=2\).
Question
\(f(x)=x^{2}\), \(-2\leq x \leq 1\). Partition the interval \([-2,1]\) as follows: \([-2,-1]\), \([-1,0]\), \([0,1]\) and choose \(u_{1}={-}{\dfrac{3}{2}}\), \(u_{2}={-}{\dfrac{1}{2}}\), \(u_{3}={\dfrac{1}{2}}\).
360
Question
\({f(x)=x^{2}}\), \(1\leq x\leq 2\). Partition the interval \([1,2]\) as follows: \(\left[1,\dfrac{5}{4}\right]\), \(\left[\dfrac{5}{4},\dfrac{3}{2}\right]\), \(\left[\dfrac{3}{2},\dfrac{7}{4}\right]\), \(\left[\dfrac{7}{4},2\right]\) and choose \(u_{1}=\dfrac{5}{4}\), \(u_{2}=\dfrac{3}{2}\), \(u_{3}=\dfrac{7}{4}\), \(u_{4}=2\).
In Problems 13 and 14, the graph of a function \(f\) defined on an interval \([a,b] \) is given.
- Partition the interval \([a,b] \) into six subintervals (not necessarily of the same size using the points shown on each graph).
- Approximate \(\int_{a}^{b}f(x)\, dx\) by choosing \(u_{i}\) as the left endpoint of each subinterval and using Riemann sums.
- Approximate \(\int_{a}^{b}f(x)\, dx\) by choosing \(u_{i}\) as the right endpoint of each subinterval and using Riemann sums.
Question
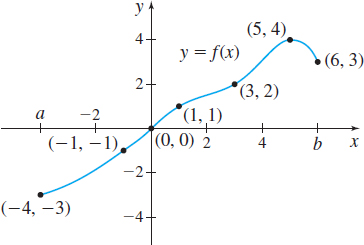
Question
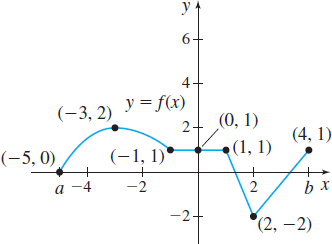
In Problems 15–22, write the limit of the Riemann sums as a definite integral. Here \(u_i\) is in the integral \([x_{i-1}, x_i]\), \(i = 1, 2, \ldots n\).
Question
\(\lim\limits_{{\max \Delta x}_{i} \rightarrow 0}\sum\limits_{i=1}^{n}\left(e^{u_{i}}+2\right) \Delta x_{i}\) on \([0,2] \)
Question
\(\lim\limits_{{\max \Delta x}_{i}\rightarrow 0}\sum\limits_{i=1}^{n}\ln u_{i}\Delta x_{i}\) on \([1,8]\)
Question
\(\lim\limits_{{\max \Delta x}_{i} \rightarrow 0}\sum\limits_{i=1}^{n}\cos u_{i}\Delta x_{i}\) on \([0,2\pi] \)
Question
\(\lim\limits_{{\max \Delta x}_{i} \rightarrow 0}\sum\limits_{i=1}^{n}\left( \cos u_{i}+\sin u_{i}\right) \Delta x_{i}\) on \([0,\pi] \)
Question
\( \lim\limits_{{\max \Delta x}_{i} \rightarrow 0}\sum\limits_{i=1}^{n}{\dfrac{{2}}{{u^{2}_i}}}\Delta x_{i}\) on \([1,4] \)
Question
\(\lim\limits_{{\max \Delta x}_{i} \rightarrow 0}\sum\limits_{i=1}^{n}u^{1/3}_i\Delta x_{i}\) on \([0,8]\)
Question
\(\lim\limits_{{\max \Delta x}_{i} \rightarrow 0}\sum\limits_{i=1}^{n}u_{i}\ln u_{i}\) \(\Delta x_{i}\) on \([1, e]\)
Question
\(\lim\limits_{{\max \Delta x}_{i} \rightarrow 0} \sum\limits_{i=1}^{n}\ln (u_{i}+1)\Delta x_{i}\) on \([0, e] \)
In Problems 23–28, find each definite integral.
Question
\(\int_{-3}^{4}e\,dx \)
Question
\(\int_{0}^{3}(-\pi) \,dx\)
Question
\(\int_{3}^{0}(-\pi)\, dt\)
Question
\(\int_{7}^{2}2\, ds\)
Question
\(\int_{4}^{4}2\, \theta\ d\theta \)
Question
\(\int_{-1}^{-1}8\, dr\)
In Problems 29–32, the graph of a function is shown. Express the shaded area as a definite integral.
Question
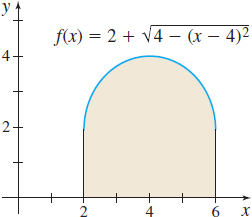
Question
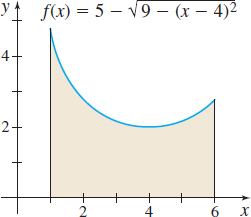
Question

Question
In Problems 33–38, determine which of the following definite integrals can be interpreted as area. For those that can, describe the area; for those that cannot, explain why.
Question
\(\int_{0}^{\pi }\sin x\,dx\)
Question
\(\int_{-\pi /4}^{\pi /4}\tan x\,dx\)
Question
\(\int_{1}^{4}(x-2) ^{1/3}dx\)
Question
\(\int_{1}^{4}(x+2) ^{1/3}dx\)
Question
\(\int_{1}^{4}(\vert x \vert \,-2 ) \,dx\)
Question
\(\int_{-2}^{4}\vert x \vert \,\,dx\)
In Problems 39–44:
- For each function defined on the given interval, use a regular partition to form Riemann sums \(\sum\limits_{i=1}^{n} f(u_{i})\Delta x_{i}\).
- Express the limit as \(n\rightarrow \infty\) of the Riemann sums as a definite integral.
 Use a computer algebra system to find the value of the definite integral in (b).
Use a computer algebra system to find the value of the definite integral in (b).
Question
\(f(x) =x^{2}-1\) on \([0,2]\)
Question
\(f(x) =x^{3}-2\) on \([0,5]\)
Question
\(f(x) =\sqrt{x+1}\) on \([0,3] \)
Question
\(f(x) =\sin x\) on \([0, \pi] \)
Question
\(f(x) =e^{x}\) on \([0, 2] \)
Question
\(f(x) =e^{-x}\) on \([0,1] \)
361
In Problems 45 and 46, find each definite integral using Riemann sums.
Question
\({\int_{0}^{1}(x - 4)dx} \)
Question
\(\int_{0}^{3}{(3x - 1)dx}\)
![]() In Problems 47–50, for each function defined on the interval \([a,b]\):
In Problems 47–50, for each function defined on the interval \([a,b]\):
- Complete the table of Riemann sums using a regular partition of \([a,b]\).
\(n\) \(10\) \(50\) \(100\) Using left endpoints Using right endpoints Using the midpoint - Use a CAS to find the definite integral.
Question
\(f(x) =2+\sqrt{x}\) on \([1,5] \)
Question
\(f(x) =e^{x}+e^{-x}\) on \([-1,3] \)
Question
\(f(x) =\dfrac{3}{1+x^{2}}\) on \([-1,1] \)
Question
\(f(x) = \dfrac{1}{\sqrt{x^2+4}} \) on \([0,2] \)
Applications and Extensions
Question
Find an approximate value of \({\int_{1}^{2}}\dfrac{1}{x}\,{dx}\) by finding Riemann sums corresponding to a partition of \([1,2]\) into four subintervals, each of the same length, and evaluating the integrand at the midpoint of each subinterval. Compare your answer with the true value, \(0.6931\ldots .\)
Question
![]()
- Find the approximate value of \({\int_{0}^{2} \sqrt{4 - x^{2}}}\,dx\) by finding Riemann sums corresponding to a partition of \([0, 2]\) into 16 subintervals, each of the same length, and evaluating the integrand at the left endpoint of each subinterval.
- Can \(\int_{0}^{2}\sqrt{4-x^{2}}\, dx\) be interpreted as area? If it can, describe the area; if it cannot, explain why.
- Find the actual value of \(\int_{0}^{2}\sqrt{4-x^{2}}dx\) by graphing \(y=\sqrt{4-x^{2}}\) and using a familiar formula from geometry.
Question
Units of an Integral In the definite integral \(\int_{0}^{5}F(x)\, dx\), \(F\) represents a force measured in newtons and \(x,\) \(0\leq x\leq 5,\) is measured in meters. What are the units of \(\int_{0}^{5}F(x)\, dx?\)
Question
Units of an Integral In the definite integral \(\int_{0}^{50}C(x)\, dx\), \(C\) represents the concentration of a drug in grams per liter and \(x,\) \(0\leq x\leq 50,\) is measured in liters of alcohol. What are the units of \(\int_{0}^{50}C(x)\, dx?\)
Question
Units of an Integral In the definite integral \(\int_{a}^{b}v(t)\, dt,\) \(v\) represents velocity measured in meters per second and time \(t\) is measured in seconds. What are the units of \(\int_{a}^{b}v(t)\, dt?\)
Question
Units of an Integral In the definite integral \(\int_{a}^{b}S(t)\, dt\), \(S\) represents the rate of sales of a corporation measured in millions of dollars per year and time \(t\) is measured in years. What are the units of \(\int_{a}^{b}S(t)\, dt?\)
Question
![]() Area
Area
- Graph the function \(f(x) =3-\sqrt{6x-x^{2}}.\)
- Find the area under the graph of \(f\) from \(0\) to \(6.\)
- Confirm the answer to (b) using geometry.
Question
![]() Area
Area
- Graph the function \(f(x) = \sqrt{4x-x^{2}}+2.\)
- Find the area under the graph of \(f\) from \(0\) to \(4.\)
- Confirm the answer to (b) using geometry.
Question
The interval \([1,5]\) is partitioned into eight subintervals each of the same length.
- What is the largest Riemann sum of \(f(x)=x^{2}\) that can be found using this partition?
- What is the smallest Riemann sum?
- Compute the average of these sums.
- What integral has been approximated, and what is the integral's exact value?
Challenge Problems
Question
The floor function \(f(x) = \) \(\lfloor x\rfloor \) is not continuous on \([0,4].\) Show that \({\int_{0}^{4}{f(x)\,dx}}\) exists.
Question
Consider the Dirichlet function \(f,\) where \[ f(x)=\left\{ \begin{array}{@{}l@{ }l@{ }l} {1} & \hbox{if} & {x}~\hbox{is rational} \\ {0} & \hbox{if} & {x}~\hbox{is irrational} \end{array} \right. \] Show that \({\int_{0}^{1}{f(x)\,dx}}\) does not exist. (Hint: Evaluate the Riemann sums in two different ways: first by using rational numbers for \({ u}_{i}\) and then by using irrational number seak for \({ u}_{i}\).)
Question
It can be shown (with a certain amount of work) that if \(f(x)\) is integrable on the interval \([a,b],\) then so is \(\vert f(x) \vert \). Is the converse true?
Question
If only regular partitions are allowed, then we could not always partition an interval \([a,b]\) in a way that automatically partitions subintervals \([a,c] \) and \([c,b]\) for \(a\lt c\lt\,b\). Why not?
Question
If \(f\) is a function that is continuous on a closed interval \([a,b] \), except at \(x_{1},\) \(x_{2},\) \( \ldots \), \(x_{n},\) \(n\geq 1\) an integer, where it has a jump discontinuity, show that \(f\) is integrable on \([a,b] .\)
Question
If \(f\) is a function that is continuous on a closed interval \([a,b] \), except at \(x_{1},\) \(x_{2},\) \( \ldots \), \(x_{n},\) \(n\geq 1\) an integer, where it has a removable discontinuity, show that \(f\) is integrableon \([a,b] .\)
