Question

According to Part 1 of the Fundamental Theorem of Calculus, if a function \(f\) is continuous on a closed interval \([a,b] \), then \(\dfrac{d}{dx}\left[\int_{a}^{x}f(t)\, dt\right] =\) _________ for all numbers \(x\) in \((a,b)\).

Question

True or False  By Part 2 of the Fundamental Theorem of Calculus, \(\int_{a}^{b} x\, dx= b-a\).

Question

True or False  By Part 2 of the Fundamental Theorem of Calculus, \(\int_{a}^{b}f(x)\, dx=f(b)-f(a).\)

Question

True or False  \(\int_{a}^{b} F^\prime (x) dx\) can be interpreted as the rate of change in \(F\) from \(a\) to \(b.\)

Question

\(\dfrac{d}{dx}{\int_{1}^{x}{\sqrt{t^{2}+1}\,dt}}\)

Question

\(\dfrac{d}{dx}\int_{3}^{x}\dfrac{t+1}{t}dt \)

Question

\(\dfrac{d}{dt}\left[\int_{0}^{t}{(3+x^{2})^{3/2}dx}\right] \)

Question

\(\dfrac{d}{dx}\left[\int_{-4}^{x}\left({t^{3}+8}\right)^{1/3}dt\right]\)

Question

\(\dfrac{d}{dx}\left[\int_{1}^{x}\ln u \,{du}\right]\)

Question

\(\dfrac{d}{dt}\left[\int_{4}^{t}e^{x}{dx}\right] \)

Question

\(\dfrac{d}{dx}\left[\int_{1}^{2x^{3}} \sqrt{t^{2}+1}\,dt \right] \)

Question

\(\dfrac{d}{dx}\left[\int_{1}^{\sqrt{x}}\sqrt{t^{4}+5} dt \right] \)

Question

\(\dfrac{d}{dx}\left[\int_{2}^{x^{5}}{\sec t} dt \right] \)

Question

\(\dfrac{d}{dx}\left[\int_{3}^{1/x}{\sin }^{5}t dt \right] \)

Question

\(\dfrac{d}{dx}\left[\int_{x}^{5}\sin ({t}^{2} ) \,dt \right] \)

Question

\(\dfrac{d}{dx}\left[\int_{x}^{3}{({t^{2}-5})^{10}\,dt} \right] \)

Question

\(\dfrac{d}{dx}\left[\int_{5x^{2}}^{5}(6t)^{2/3}\,dt \right] \)

Question

\(\dfrac{d}{dx}\left[\int_{x^{2}}^{0}e^{10t}\,dt \right]\)

Question

\(\int_{-2}^{3}{dx} \)

Question

\(\int_{-2}^{3}{2\,dx} \)

Question

\(\int_{-1}^{2}{x^{3}dx} \)

Question

\(\int_{1}^{3}{\dfrac{1}{x^{3}}dx}\)

Question

\(\int_{0}^{1}\sqrt{u}\,du \)

Question

\(\int_{1}^{8}{\sqrt[3]{{y}}\,dy}\)

Question

\(\int_{\pi /6}^{\pi /2} \csc ^{2}{x\,dx} \)

Question

\(\int_{0}^{\pi /2}{\cos x\,dx}\)

Question

\(\int_{0}^{\pi /4}\sec x\tan x~dx\)

Question

\(\int_{\pi /6}^{\pi /2}\csc x\cot x\,dx\)

Question

\(\int_{-1}^{0}e^{x}dx \)

Question

\(\int_{-1}^{0}e^{-x}dx \)

Question

\(\int_{1}^{e}\dfrac{1}{x}dx\)

Question

\(\int_{e}^{1}\dfrac{1}{x}dx \)

Question

\(\int_{0}^{1}\dfrac{1}{1+x^{2}}dx \)

Question

\(\int_{0}^{\sqrt{2}/2}\dfrac{1}{\sqrt{1-x^{2}}}dx\)

Question

\(\int_{-1}^{8}x^{2/3}\,dx\)

Question

\(\int_{0}^{4}x^{3/2}\,dx\)

Question

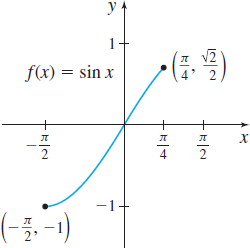
Question

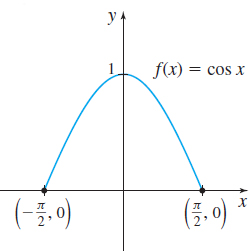
Question

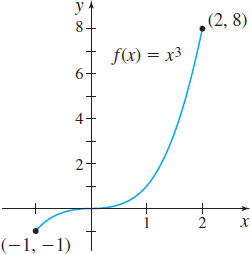
Question

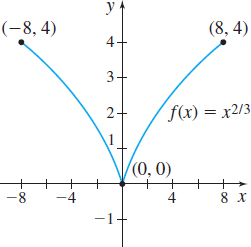
Question

Question

Question

Given that \(f(x)=(2x^{3}-3)^{2}\) and \(f^\prime (x) =12x^{2}(2x^{3}-3),\) find \(\int_{0}^{2}[12x^{2}(2x^{3}-3)]\, dx.\)

Question

Given that \(f(x)=(x^{2}+5)^{3}\) and \(f^\prime (x) =6x(x^{2}+5) ^{2},\) find \(\int_{-1}^{2}{6x(x^{2}+5)^{2}\, dx.}\)

Question

Area Find the area under the graph of \(f(x) =\dfrac{1}{\sqrt{1-x^{2}}}\) from \(0\) to \(\dfrac{1}{2}.\)

Question

Area Find the area under the graph of \(f(x) =\cosh x\) from \(-1\) to \(1\).

Question

Area Find the area under the graph of \(f(x) =\dfrac{1}{x^{2}+1}\) from \(0\) to \(\sqrt{3}.\)

Question

Area Find the area under the graph of \(f(x) =\dfrac{1}{1+x^{2}}\) from \(0\) to \(r\), where \(r>0\). What happens as \(r\rightarrow \infty \)?

Question

Area Find the area under the graph of \(y=\dfrac{1}{\sqrt{x}} \) from \(x=1\) to \(x=r\), where \(r>1\). Then examine the behavior of this area as \(r\rightarrow \infty \).

Question

Area Find the area under the graph of \(y=\dfrac{1}{x^{2}}\) from \(x=1\) to \(x=r\), where \(r>1\). Then examine the behavior of this area as \(r\rightarrow \infty \).

Question

Interpreting an Integral The function \(R=R(t) \) models the rate of sales of a corporation measured in millions of dollars per year as a function of the time \(t\) in years. Interpret the integral \(\int_{0}^{2}R(t)\,dt=23\).

Question

Interpreting an Integral The function \(v=v( t) \) models the speed \(v\) in meters per second of an object at a time \(t\) in seconds. Interpret the integral \(\int_{0}^{10}v(t)\,dt=4.8.\)

Question

Interpreting an Integral Helium is leaking from a large advertising balloon at a rate of \(H(t) \) cubic centimeters per minute, where \(t\) is measured in minutes.

1. Write an integral that models the change in helium in the balloon over the interval \(a\leq t\,\leq b.\)
2. What are the units of the integral from (a)?
3. Interpret \(\int_{0}^{300}H(t)\, dt=-100.\)

Question

Interpreting an Integral Water is being added to a reservoirat a rate of \(w(t) \) kiloliters per hour, where \(t\) is measured in hours.

1. Write an integral that models the change in amount of water in the reservoir over the interval \(a\leq t\,\leq b.\)
2. What are the units of the integral from (a)?
3. Interpret \(\int_{0}^{36}w(t)\, dt=800.\)

Question

Free Fall  The speed \(v\) of an object dropped from rest is given by \(v(t) =9.8t\), where \(v\) is in meters per second and time \(t\) is in seconds.

1. Express the distance traveled in the first \(5.2\) s as an integral.
2. Find the distance traveled in \(5.2\) s.

Question

Area  Find \(h\) so that the area under the graph of \(y^{2}=x^{3}, 0\leq x\leq 4, y\geq 0\), is equal to the area of a rectangle of base \(4\) and height \(h\).

Question

Area  If \(P\) is a polynomial that is positive for \(x>0\), and for each \(k>0\) the area under the graph of \(P\) from \(x=0\) to \(x=k\) is \(k^{3}+3k^{2}+6k\), find \(P\).

Question

Put It Together  If \(f(x)={\int_{0}^{x}}\dfrac{{1}}{\sqrt{t^{3}+2}}\,dt\), which of the following is false?

1. \(f\) is continuous at \(x\) for all \(x\geq 0\)
2. \(f(1)>0\)
3. \(f(0) =\dfrac{1}{\sqrt{2}}\)
4. \(f^\prime (1)=\dfrac{1}{\sqrt{3}}\)

Question

\(\int_{0}^{4}x^{2}dx\) and \(\int_{-4}^{4}x^{2}dx\)

Question

\(\int_{0}^{4}x^{3}dx\) and \(\int_{-4}^{4}x^{3}dx\)

Question

\(\int_{0}^{\pi /4}\sec ^{2}x\,dx\) and \(\int_{-\pi /4}^{\pi /4}\sec ^{2}x\,dx\)

Question

\(\int_{0}^{\pi /4}\sin x\,dx\) and \(\int_{-\pi /4}^{\pi /4}\sin x\,dx\)

Question

Area  Find \(c\), \(0\lt c\lt 1\), so that the area under the graph of \(y=x^2\) from 0 to \(c\) equals the area under the same graph from \(c\) to 1.

Question

Area Let \(A\) be the area under the graph of \(y=\dfrac{1}{x}\) from \(x=m\) to \(x=2m\), \(m>0\). Which of the following is true about the area \(A\)?

1. \(A\) is independent of \(m.\)
2. \(A\) increases as \(m\) increases.
3. \(A\) decreases as \(m\) increases.
4. \(A\) decreases as \(m\) increases when \(m\lt\dfrac{1}{2}\) and increases as \(m\) increases when \(m>\dfrac{1}{2}.\)
5. \(A\) increases as \(m\) increases when \(m\lt\dfrac{1}{2}\) and decreases as \(m\) increases when \(m>\dfrac{1}{2}.\)

Question

Put It Together  If \(F\) is a function whose derivative is continuous for all real \(x\), find \[ \lim\limits_{{_{h\rightarrow 0}}}{\dfrac{{1}}{{h}}}{\int_{c}^{c+h}{{F^\prime } (x)\,dx}} \]

Question

Suppose the closed interval \(\left[ 0,\dfrac{\pi }{2}\right] \) is partitioned into \(n\) subintervals, each of length \(\Delta x\), and \(u_{i}\) is an arbitrary number in the subinterval \([x_{i - 1},\,x_{i}],\) \(i\,=1,\,2,\,\ldots ,\,n\). Explain why \[ \lim\limits_{{n\,\rightarrow \,\infty }}\,{\sum\limits_{i=1}^{n}}\left[ {{({ \cos }\,u_{i})\,\Delta x}}\right] ={1} \]

Question

The interval \([0,4]\) is partitioned into \(n\) subintervals, each of length \(\Delta x\), and a number \(u_{i}\) is chosen in the subinterval \([x_{i-1},\,x_{i}],\) \(i=1,\,2,\,\ldots ,\,n\). Find \(\lim\limits_{n\rightarrow \infty }{\sum\limits_{i=1}^{n}}( e^{u_1} \Delta x) .\)

Question

If \(u\) and \(\nu \) are differentiable functions and \(f\) is a continuous function, find a formula for \[ {\dfrac{{d}}{{dx}}}{\left[ {{\int_{u(x)}^{\nu (x)}{f(t)\,dt}}}\right] } \]

Question

Suppose that the graph of \(y=f(x)\) contains the points \((0,1)\) and \((2,5) \). Find \(\int_{0}^{2}f^\prime (x)\,dx\). (Assume that \(f^\prime \) is continuous.)

Question

If \(f^\prime \) is continuous on the interval \([a,b] \), show that \[ \int_{a}^{b} f(x) f^\prime (x)\,dx=\dfrac{1}{2} \Big\{ [f(b)]^{2}-[f(a)]^{2} \Big\}. \]

[Hint: Look at the derivative of \(F(x) =\dfrac{\left[f(x) \right] ^{2}}{2}.]\)

Question

If \(f^{\prime \prime} \) is continuous on the interval \([a,b] \), show that \[ \int_{a}^{b} xf^{\prime \prime} (x)\,dx=bf^\prime (b)-a f^\prime (a)-f(b)+f(a). \]

[Hint: Look at the derivative of \(F(x)=xf^\prime (x)-f(x).\)]

Question

What conditions on \(f\) and \(f^\prime\) guarantee that \(f(x)={\int_{0}^{x}{{f^\prime }(t)\,dt}}\)?

Question

Suppose that \(F\) is an antiderivative of \(f\) on the interval \([a,b] .\) Partition \([a,b] \) into \(n\) subintervals, each of length \(\Delta x_{i}=x_{i}-x_{i-1},\) \(i=1,2,\ldots,n\).

1. Apply the Mean Value Theorem for derivatives to \(F\) in each subinterval \([x_{i-1},x_{i}]\) to show that there is a point \(u_{i}\) in the subinterval for which \(F(x_{i})-F(x_{i-1})=f(u_{i})\Delta x_{i}\).
2. Show that \(\sum\limits_{i=1}^{n}[F(x_{i})-F(x_{i-1})]=F(b)-F(a).\)
3. Use parts (a) and (b) to explain why \[ \int_{a}^{b}f(x)\,dx = F(b)-F(a). \] (In this alternate proof of Part 2 of the Fundamental Theorem of Calculus, the continuity of \(f\) is not assumed.)

Question

Given \(y=\sqrt{x^{2} - 1} (4 - x),\) \(1\leq x\leq a\), for what number \(a\) will \(\int_{1}^{a}y\,dx\) have a maximum value?

Question

Find \(a>0\), so that the area under the graph of \(y=x+\dfrac{1}{x}\) from \(a\) to \((a+1) \) is minimum.

Question

If \(n\) is a known positive integer, for what number \(c\) is \[ \int_{1}^{c}x^{n-1}\,dx=\dfrac{1}{n} \]

Question

Let \(f(x)={\int_{0}^{x}{{\dfrac{dt}{\sqrt{1-t^{2}}}}, 0 \lt x \lt 1.}}\)

1. Find \(\dfrac{d}{dx} f(\sin x).\)
2. Is \(f\) one-to-one?
3. Does \(f\) have an inverse?