6.6 Work
OBJECTIVES
When you finish this section, you should be able to:
- Find the work done by a variable force (p. 445)
- Find the work done by a spring force (p. 446)
- Find the work done to pump a liquid (p. 448)
Application to gravitational force (p. 450)
In physics, work is defined as the energy transferred to or from an object by a force acting on the object. The work \(W\) done by a constant force \(F\) in moving an object a distance \(x\) along a straight line in the direction of \(F\) is defined to be \begin{align*} \bbox[5px, border:1px solid black, #F9F7ED]{W=Fx} \end{align*}
See Figure 53.
One unit of work is the work done by a unit force in moving an object a unit distance in the direction of the force. In the International System of Units (abbreviated SI, for Système International d'Unités), the unit of work is a newton-meter, which is called a joule (J). In terms of customary U.S. units, the unit of work is the foot-pound. These terms are summarized in Table 1.
445
| Work Units | Force Units | Distance Units | |
|---|---|---|---|
| SI | joule (J) | newton (N) | meter (m) |
| U.S. | foot-pound (ft lb) | pound (lb) | foot (ft) |

ORIGINS
Joule, the unit of energy, is named for James Prescott Joule, a British physicist and brewer who lived in the 19th century.
For example, the work \(W\) required to lift an object weighing \(80\) lb a distance of \(5\) ft would be \(W=(80)(5)=400\) ft lb.
When a force \(F\) acts in the same direction as the motion, the work done is positive; if a force \(F\) acts in a direction opposite to the motion, the work done is negative.
In some cases, a force \(F\) acts along the line of motion of an object, but the magnitude of the force varies depending on the position of the object. For example, the force required to raise a cable depends on the length of the cable, and the force required to stretch a spring depends on how far the spring has already been stretched from its normal length. These are examples of variable forces.
NOTE
\(1 \textrm{ N}\) is the force required to accelerate an object of mass \(1 \textrm{ kg}\) at \(1 \textrm{ m/s}^{2}\). Also, \(1 \textrm{ J} \approx 0.7376 \textrm{ ft} \textrm{ lb}\) and \(1 \textrm{ ft} \textrm{ lb} \approx 1.356 \textrm{ J}.\)
1 Find the Work Done by a Variable Force
Suppose a variable force \(F=F(x)\) acts on an object, where \(x\) is the distance of the object from the origin and \(F\) is a function that is continuous on a closed interval \(\left[a\,,b\right]\). We seek a formula for finding the work done by the force \(F\) in moving the object from \(x=a\) to \(x=b.\) We begin by partitioning the interval \([a,b]\) into \(n\) subintervals: \begin{equation*} [ a,x_{1} ] , [ x_{1},x_{2} ] , \ldots , [ x_{i-1},x_{i} ] , \ldots , [ x_{n-1},b ] \end{equation*}
each of width \(\Delta x=\dfrac{b-a}{n}.\)
Now we consider the \(i \textrm{th}\) subinterval \([ x_{i-1}, x_{i}],\) and choose a number \(u_{i}\) in \([ x_{i-1}, x_{i}]\). If the width of the subinterval is small, the force \(F=F(x)\) acting on the object will not change much over the interval; that is, \(F\) can be treated as a constant force. Then the work \(W\) done by \(F\) to move the object from \(x_{i-1}\) to \(x_{i}\) can be approximated by \begin{align*} \bbox[5px, border:1px solid black, #F9F7ED]{ W_{i}\underset{\underset{\color{#0066A7}{\hbox{\(W=Fx\)}}}{\color{#0066A7}{\uparrow }}} {=} F(u_{i}) \Delta x } \end{align*}
Summing the work done over all the subintervals approximates the total work \(W\) done by the force \(F\) in moving an object from \(a\) to \(b\). That is, the total work \(W\) is approximated by the Riemann sums \begin{equation*} W\approx F(u_{1})\Delta x+F(u_{2})\Delta x+\cdots +F(u_{n})\Delta x=\displaystyle \sum_{i=1}^{n}F(u_{i})\Delta x \end{equation*}
As the number of subintervals increases, that is, as \(n\rightarrow \infty\), the approximation improves, and, if \(F=F(x)\) is continuous on \([a,b],\) then \begin{equation*} W=\lim\limits_{n\,\rightarrow \,\infty }\displaystyle \sum_{i=1}^{n}F(u_{i})\Delta x=\int_{a}^{b}F(x) ~{\it dx} \end{equation*}
Work
The work \(W\) done by a continuously varying force \(F\) acting on an object, which moves the object along a straight line in the direction of \(F\) from \(x=a\) to \(x=b\), is \begin{align*} \bbox[5px, border:1px solid black, #F9F7ED]{W=\int_{a}^{b}F(x)~{\it dx} } \end{align*}
446
Consider a freely hanging cable or chain that is being lengthened or shortened. The weight of the cable is a function of its length. As the cable is let out, its weight increases proportionally to its length, and when it is pulled in, it decreases proportionally to its length.
Finding the Work Done in Pulling in a Rope
A \(60\)-ft rope weighing \(8\) lb per linear foot is used for mooring a cruise ship. See Figure 54. As the ship prepares to leave port, the rope is released, and it hangs freely over the side of the ship. How much work is done by the deckhand who winds in the rope?

Solution We position an \(x\)-axis parallel to the side of the ship with the origin \(O\) of the axis even with the bottom of the rope and \(x=60\) even with the ship's deck. The work done by the deckhand depends on the weight of the rope and the length of rope hanging over the edge.
Partition the interval \([ 0,60]\) into \(n\) subintervals, each of length \(\Delta x=\dfrac{60}{n}\), and choose a number \(u_{i}\) in each subinterval. Now think of the rope as \(n\) short segments, each of length \(\Delta x.\) Then \[ \begin{array}{rcl} \hbox{Weight of the }i{\rm th}\hbox{ segment } &=&8\Delta x\textrm{lb}\\ \hbox{Distance the }i{\rm th}\hbox{ segment is lifted } &=&(60-u_{i}) \textrm{ft}\\ \hbox{Work done in lifting the }i{\rm th}\hbox{ segment } &=&8(60-u_{i}) \Delta x\ \textrm{ft}~\textrm{lb} \qquad {\color{#0066A7}{\hbox{$W=Fx$}}} \end{array} \]
The work \(W\) required to lift the \(60\textrm{ ft}\) of rope is \[ W=\int_{0}^{60}8( 60-x) ~{\it dx}=\big[ 480x-4x^{2}\big]_{0}^{60}=14{,}400~\textrm{ft}~\textrm{lb} \]
NOW WORK
Problem 11.
2 Find the Work Done by a Spring Force
A common example of the work done by a variable force is found in stretching or compressing a spring that is fixed at one end. A spring is said to be in equilibrium when it is neither extended nor compressed. The spring force \(F\) needed to extend or compress a spring depends on the stiffness of the spring, which is measured by its spring constant \(k\), a positive real number. Since a spring always attempts to return to equilibrium, a spring force \(F\) is often called a restoring force. A spring force \(F\) varies with the distance \(x\) that the free end of the spring is moved from its equilibrium length and obeys Hooke's Law: \begin{align*} \bbox[5px, border:1px solid black, #F9F7ED]{ F(x)=-kx } \end{align*}
where \(k\) is the spring constant measured in newtons per meter in SI units or pounds per foot in U.S. units. The minus sign in Hooke's Law indicates that the direction of a spring force is opposite from the direction of the displacement.
As Figure 55 illustrates, the distance \(x\) in Hooke's Law is measured from the equilibrium, or unstretched, position of the spring. This distance \(x\) is positive if the spring is stretched from its equilibrium position and is negative if the spring is compressed from its equilibrium position. As a result, a spring force \(F\) is negative if the spring is stretched and \(F\) is positive if the spring is compressed.

In applied problems involving springs, the value of \(k,\) the spring constant, is often unknown. When we know information about how the spring behaves, the value of \(k\) can be found. The next example illustrates this.
447
Analyzing a Spring Force
Suppose a spring in equilibrium is \(0.8\textrm{ m}\) long and a spring force of \(2\textrm{ N}\) stretches the spring to a length of \(1.2\textrm{ m}.\)
- Find the spring constant \(k\) and the spring force \(F\).
- What spring force is required to stretch the spring to a length of \(3\textrm{ m}\)?
- How much work is done by the spring force in stretching it from equilibrium to \(3\textrm{ m}\)?
Solution We position an axis parallel to the spring and place the origin at the free end of the spring in equilibrium, as in Figure 56.
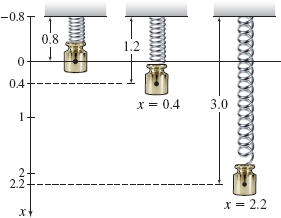
- When the spring is stretched to a length of \(1.2\textrm{ m}\), then \(x=0.4\). Using Hooke's Law, we get \begin{eqnarray*} -2 &=&-k( 0.4) \qquad\quad {\color{#0066A7}{\hbox{Hooke's law:} F(x)=-kx; F=-2; x=0.4}} \\[4pt] k &=&\dfrac{2}{0.4}=5\textrm{N}/\textrm{ m} \end{eqnarray*} The spring constant is \(k=5\). The spring force \(F\) is \(F=-kx=-5x.\)
- The spring force \(F\) required to stretch the spring to a length of \(3\textrm{ m}\), that is, a distance \(x=3-0.8=2.2\textrm{ m}\) from equilibrium, is \[ F=-5x=( -5) ( 2.2) =-11\textrm{ N} \]
- The work \(W\) done by the spring force \(F\) when stretching the spring from equilibrium \((x=0)\) to \(x=2.2\) is \[ \begin{eqnarray*} W&=&\int_{0}^{2.2}F(x) {\it dx} \underset{\underset{\color{#0066A7}{\hbox{\(F(x) = -5x\)}}}{\color{#0066A7}{\uparrow }}} {=} -5\int_{0}^{2.2}x\,{\it dx}= -5\left[ \dfrac{x^{2}}{2} \right] _{0}^{2.2}=-\dfrac{5}{2}(4.84)=-12.1\textrm{ J} \nonumber\\[-11pt] && \end{eqnarray*} \]
Finding the Work Done by a Spring Force
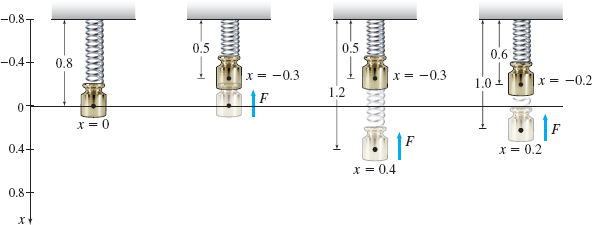
Suppose an 0.8 m-long spring has a spring constant of \(k=5\textrm{ N}/\textrm{ m}\).
- What spring force is required to compress the spring from its equilibrium position to a length of \(0.5\textrm{ m}\)?
- How much work is done by the spring force when compressing the spring from equilibrium to a length of \(0.5\textrm{ m}\)?
- How much work is done by the spring force when compressing the spring from 1.2 to \(0.5\textrm{ m}\)?
- How much work is done by the spring force when compressing the spring from 1 to \(0.6\textrm{ m}\)?
Solution We begin by positioning an axis parallel to the spring and placing the origin at the free end of the spring in equilibrium. See Figure 57.
448
- By Hooke's Law, the spring force is \(F=-5x\). When the spring is compressed to a length of \(0.5\textrm{ m}\), then \(x=-0.3\) The spring force \(F\) required to compress the spring to \(0.5\textrm{ m}\) is \[ F=-kx=-5( -0.3) =1.5\hbox{ }\textrm{N} \]
- The work \(W\) done by the spring force \(F\) when compressing the spring from equilibrium \((x=0)\) to \(x=-0.3\) is \begin{eqnarray*} W&=&\int_{0}^{-0.3}F(x) {\it dx}\underset{\underset{\color{#0066A7}{\hbox{\(F(x) = -5x\)}}}{\color{#0066A7}{\uparrow }}} {=}\int_{0}^{-0.3}\left( -5x\right) {\it dx} = 5\int_{-0.3}^{0}x\,{\it dx}= 5 \left[\dfrac{x^{2}}{2}\right] _{-0.3}^{0}\\[-11pt] &=&0-\dfrac{5\,\left( -0.3\right) ^{2}}{2}=-0.225\textrm{ J} \end{eqnarray*}
- The work \(W\) done by the spring force \(F\) when compressing the spring from \(1.2\textrm{ m}\) \((x=0.4)\) to \(x=-0.3\) is \begin{equation*} W=\int_{0.4}^{-0.3}( -5x) \,{\it dx}=5\int_{-0.3}^{0.4}x\,{\it dx}= 5 \left[\dfrac{x^{2}}{2}\right] _{-0.3}^{0.4}=\dfrac{5}{2}[ 0.4^{2}-( -0.3) ^{2}] =0.175\textrm{ J} \end{equation*}
- The work \(W\) done when compressing the spring from \(1\textrm{ m} \ (x=0.2)\) to \(0.6\textrm{ m}\) \((x =-0.2)\) is \[ W=\int_{0.2}^{-0.2}( -5x) \,{\it dx}=5\int_{-0.2}^{0.2}x\,{\it dx}= 5 \left[\dfrac{x^{2}}{2}\right] _{-0.2}^{0.2}=\dfrac{5}{2}[ 0.2^{2}-(-0.2) ^{2}] =0\textrm{ J} \]
Observe that the work \(W\) done by a spring force can be positive, negative, or zero. If the force brings the spring closer to its equilibrium position \((x=0)\), then \(W>0;\) if the force brings the spring away from its equilibrium position, then \(W<0.\) If the spring ends up the same distance from the equilibrium, then no work is done; that is, \(W=0.\)
NOW WORK
Problem 15.
3 Find the Work Done to Pump a Liquid
Another example of work done by a variable force is found in the work needed to pump a liquid out of a tank. The idea used is that the work needed to lift an object a given distance is the product of the weight (force) of the object and the distance it is lifted, that is, \begin{equation*} \hbox{Work}=\hbox{(Weight of object)(Distance lifted)} \end{equation*}

Finding the Work Required to Pump Oil out of a Tank
An oil tank in the shape of a right circular cylinder, with height \(30\textrm{ m}\) and radius \(5\textrm{ m}\), is two-thirds full of oil. How much work is required to pump all the oil over the top of the tank?
Solution We position an \(x\)-axis parallel to the side of the cylinder with the origin of the axis even with the bottom of the tank and \(x=30\) at the top of the tank, as illustrated in Figure 58.
The work required to pump the oil over the top is the product of the weight of the oil and its distance from the top of the tank. The weight of the oil equals \(\rho gV\) newtons, where \(\rho \approx 820\) \(\textrm{ kg} \textrm{/m}^{3}\) is the mass density of petroleum (mass per unit volume, a constant that depends on the type of liquid involved), \(g\approx 9.8\textrm{ m} \textrm{/s} ^{2}\) (the acceleration due to gravity), and \(V\) is the volume of the liquid to be moved. The weight of the oil is \[ \hbox{Weight }=\rho gV\approx \hbox{ }( 820) ( 9.8) V=8036V\,\textrm{N} \]
449
The oil fills the tank from \(x=0\textrm{ m}\) to \(x=20\textrm{ m}\). We partition the interval \([ 0,20]\) into \(n\) subintervals, each of width \(\Delta x=\dfrac{20}{n}\). Consider the oil in the \(i\)th subinterval as a thin layer of thickness \(\Delta x\). Now choose a number \(u_{i}\) in the \(i {th}\) subinterval. Then \begin{align*} \hbox{Volume }V_{i}\hbox{ of }i{\hbox{th}}\hbox{ layer} & =(\hbox{Area of layer})(\hbox{Thickness})=\pi r^{2}\Delta x=25\pi \Delta x \\ \hbox{Weight of }i{\hbox{th}}\hbox{ layer} & =\rho gV_{i}\approx (8036) (25\pi \Delta x)=200{,}900\pi \Delta x \\ \hbox{Distance }i{\hbox{th}}\hbox{ layer is lifted} & =30-u_{i} \\ \hbox{Work }W_{i}\hbox{done in lifting }i{\hbox{th}}\hbox{ layer} & \approx ( 200{,}900\pi \Delta x) ( 30-u_{i}) \end{align*}
NOTE
\[ \begin{array}{rcl} \hbox{Weight} &=& \hbox{(Mass density)(Acceleration}\\ &&\hbox{due to gravity)(Volume)} = \rho gV \end{array} \]
Mass density \(\rho\) is often shortened to density when using SI units, since kilograms, a measure of mass, is the basic unit. When using customary U.S. units, however, we use weight density since a pound is a measure of weight. (In U.S. units, the unit of mass is called a slug. \(1 \text{slug}=32.2\textrm{ lb}\).)
The layers of oil are from 0 to \(20\textrm{ m}\). So, the work \(W\) required to pump all the oil over the top is \begin{eqnarray*} W &=&\displaystyle \int_{0}^{20}200{,}900\pi ( 30-x) \,{\it dx}=200{,}900\pi \displaystyle \int_{0}^{20}( 30-x) \,{\it dx}\\[3pt] &=&( 200{,}900~\pi )\! \left[30x-\frac{x^{2}}{2} \right] _{0}^{20} \notag \\[3pt] &=&( 200{,}900~\pi ) (600-200)=80{,}360{,}000\pi \approx 2.525\times 10^{8} \textrm{ J}\ \quad \end{eqnarray*}

Finding the Work Required to Pump Water from a Tank
A water tank in the shape of a hemisphere of radius \(2\textrm{ m}\) is full of water. How much work is required to pump all the water to a level \(3\textrm{ m}\) above the tank?
Solution We position an \(x\)-axis so the bottom of the tank is at \(x=0\) and the top of the tank is at \(x=2\), as illustrated in Figure 59(a).*
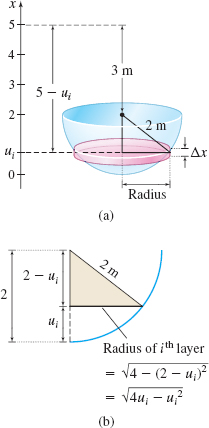
The work required to pump the water to a level \(3\textrm{ m}\) above the top of the tank depends on the weight of the water and its distance from a level \(3\textrm{ m}\) above the tank. The water fills the container from \(x=0\) to \(x=2.\)
Partition the interval \([ 0, 2]\) into \(n\) subintervals, each of width \(\Delta x=\dfrac{2}{n}\), and choose a number \(u_{i}\) in each subinterval. Now think of the water in the tank as \(n\) circular layers, each of thickness \(\Delta x\). As Figure 59(b) illustrates, the radius of the circular layer \(u_{i}\) meters from the bottom of the tank is \(\sqrt{4u_{i}-u_{i}^{2}}\). Then \begin{align*} \hbox{Volume }V_{i}\hbox{ of }i{\hbox{th }}\hbox{layer}&=\pi (\hbox{Radius} )^{2}\hbox{(Thickness)}\\[5pt] &=\pi \Big( \sqrt{4u_{i}-u_{i}^{2}}\Big) ^{2}\Delta x =\pi \big( 4u_{i}-u_{i}^{2}\big) \Delta x \end{align*}
The density of water is \(\rho =1000\textrm{ kg} \textrm{/m}^{3},\) so \begin{align*} \hbox{Weight of }i{\hbox{th }}\hbox{layer} & =\rho gV_{i}=(1000) ( 9.8) \pi \big(4u_{i}-u_{i}^{2}\big)\Delta x\, \\ \hbox{Distance }i{\hbox{th}}\hbox{ layer is lifted} & =5-u_{i} \\ \hbox{Work done in lifting }i{\hbox{th}}\hbox{ layer} & =9800\,\pi \big(4u_{i}-u_{i}^{2}\big)(5-u_{i})~\Delta x \end{align*}
The work \(W\) required to lift all the water from the tank to a level 3 m above the top of the tank is given by \begin{eqnarray*} W &=&\int_{0}^{2}9800~\pi (4x-x^{2})(5-x)~{\it dx}=9800\pi \displaystyle \int_{0}^{2}(x^{3}-9x^{2}+20x) ~{\it dx} \notag \\[5pt] &=&9800~\pi \left[ \dfrac{x^{4}}{4}-3x^{3}+10x^{2}\right] _{0}^{2}=196{,}000\pi \approx 615{,}752~\textrm{J} \end{eqnarray*}
*The choice of \(x=0\) for the position of the bottom of the tank is one of convenience. The work will be the same for other choices of \(x\) for the bottom of the tank.
450
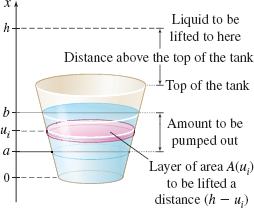
In general, to find the work required to pump liquid from a container, think of the liquid as thin layers of thickness \(\Delta x\) and area \(A(x)\). If the liquid is to be lifted a height \(h\) above the bottom of the tank, the work required is \begin{eqnarray*} \bbox[5px, border:1px solid black, #F9F7ED]{ W=\int_{a}^{b}\rho gA(x)(h-x)~{\it dx} } \end{eqnarray*}
where \(\rho\) is the density of the liquid, \(g\) is the acceleration due to gravity, and the liquid to be lifted fills the container from \(x=a\) to \(x=b\). See Figure 60.
NOW WORK
Problem 17.
Application to Gravitational Force
In the mid-1600s, Isaac Newton proposed his theory of gravity. Newton's Law of Universal Gravitation states that every body in the universe attracts every other body; he called this force gravitation . Newton theorized that the gravitational force \(F\) attracting two bodies is proportional to the masses of both bodies and inversely proportional to the square of the distance \(x\) between them. That is, \begin{align*} \bbox[5px, border:1px solid black, #F9F7ED]{ F=F(x) =G\dfrac{m_{1} m_{2}}{x^{2}} } \end{align*}

where \(G\) is the gravitational constant. The widely accepted value of \(G\), \begin{align*} \bbox[5px, border:1px solid black, #F9F7ED]{ G=6.67\times 10^{-11} \dfrac{\textrm{Nm}^{2}}{\textrm{kg}^{2}} } \end{align*}
is a result of the work done by Henry Cavendish in 1798.
ORIGINS
Henry Cavendish (1731–1810) was an English chemist and physicist. Known for his precision and accuracy, Cavendish calculated the density of Earth by measuring the force of the attraction between pairs of lead balls. An immediate result of his experiments was the first calculation of the gravitational constant \(G.\)
In a paper appearing in Science (2007, January 5), 315(5808), 74–77, the measurement was reevaluated using atom interferometry to be \(G=6.693\times 10^{-11} \dfrac{\textrm{ N} \textrm{ m}^{2}}{\textrm{ kg}^{2}}.\)
One of the conclusions of Newton's Law of Universal Gravitation is that the force required to move an object, say, a rocket of mass \(m\) kilograms that is at a point \(x\) meters above the center of Earth, is \(F(x)=G~\dfrac{M m }{x^{2}}\), where \(M\) kilograms is the mass of Earth. Then the work required to move an object of mass \(m\) from the surface of Earth to a distance \(r\) meters from the center of Earth (where \(R\) meters is the radius of Earth) is \begin{eqnarray*} W&=&\int_{R}^{r}\left[ G~\frac{M m}{x^{2}}\right] ~{\it dx}= -G \left[\frac{ M m}{x}\right] _{R}^{r}=G~\frac{M m}{R}-G~\frac{M m}{~r}\\ &=&G M m\left( \frac{1}{R}-\frac{1}{r}\right)\! \textrm{ J} \end{eqnarray*}
Physicists know that \(G M=gR^{2}\), where \(g\approx 9.8\textrm{ m}/\textrm{s}^{2}\) is the acceleration due to gravity of Earth and \(R\approx 6.37\times 10^{6}\textrm{ m}\). If \(d\) is the distance the object is to be moved above the surface of Earth, then \(r= R+d\). So, the work required to move an object of mass \(m\) to a distance \(d\) meters above the surface of Earth is \begin{equation*} W=gRm\left( 1-\frac{R}{R+d}\right) \end{equation*} Observe that although the distance \(d\) may be extremely large, the work \(W\) required to move an object \(d\) meters will never be greater than \(gRm\approx ( 6.24\times 10^{7}) m\textrm{ J}\).