Question

True or False Work is the energy transferred to or from an object by a force acting on the object.

Question

The work \(W\) done by a constant force \(F\) in moving an object a distance \(x\) along a straight line in the direction of \(F\) is _____.

Question

A unit of work is called a _____, in SI units and a _____-_____, in the customary U.S. system of units.

Question

The work \(W\) done by a continuously varying force \(F=F(x)\) acting on an object, which moves the object along a straight line in the direction of \(F\) from \(x=a\) to \(x=b\), is given by the definite integral _____.

451

Question

A spring is said to be in _____when it is neither extended nor compressed.

Question

True or False The force \(F\) required to extend or compress a spring when it is either extended or compressed \(x\) units is \(F=-kx,\) where \(k\) is the spring constant.

Question

True or False The mass density \(\rho \) of a fluid is defined as mass per unit volume (\(\textrm{ kg/m}^{3}\)) and is a constant that depends on the type of fluid.

Question

True or False Newton's Law of Universal Gravitation affirms that every body in the universe attracts every other body, and that the force \(F\) attracting two bodies is proportional to the product of the masses of both bodies and inversely proportional to the square of the distance between them.

Question

How much work is done by a variable force \(F(x)=\left( 40-x\right) \textrm{ N}\) that moves an object along a straight line in the direction of \(F\) from \(x=5\textrm{ m}\) to \(x=20\textrm{ m}\)?

Question

How much work is done by a variable force \(F(x) =\dfrac{1}{x}{N}\) that moves an object along a straight line in the direction of \(F\) from \(x=1\textrm{ m}\) to \(x=2\textrm{ m}\)?

Question

A 40 m chain weighing \(3\textrm{ kg/m}\) hangs over the side of a bridge. How much work is done by a winch that winds the entire chain in?

Question

A 120 ft chain weighing 240 lb is dangling from the roof of an apartment building. How much work is done in pulling the entire chain up to the roof?

Question

A force of \(3\textrm{ N}\) is required to keep a spring extended \(\dfrac{1}{4}\textrm{ m}\) beyond its equilibrium length. What is its spring constant?

Question

A force of 6 lb is required to keep a spring compressed to \(\dfrac{1}{2}\textrm{ ft}\) shorter than its equilibrium length. What is its spring constant?

Question

A spring with spring constant \(k=5\) has an equilibrium length of \(0.8\textrm{ m}\). How much work is required to stretch the spring to \(1.4\textrm{ m}\)?

Question

A spring with spring constant \(k= 0.3\) has an equilibrium length of \(1.2\textrm{ m}\). How much work is required to compress the spring to\(1\textrm{ m}\)?

Question

Pumping Water out of a Pool A swimming pool in the shape of a right circular cylinder, with height \(4\textrm{ ft}\) and radius \(12\textrm{ ft}\), is full of water. See the figure below. How much work is required to pump all the water over the top of the pool? (The weight density of water is \(62.42\textrm{ lb/ft}^{3}\).

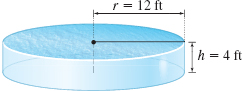
Question

Pumping Gasoline out of a Tank A gasoline storage tank in the shape of a right circular cylinder, with height \(10\textrm{ m}\) and radius \(8\textrm{ m}\), is full of gasoline. How much work is required to pump all the gasoline over the top of the tank? (The density of gasoline is \(\rho =720\textrm{ kg/m}^{3}\).)

Question

Pumping Corn Slurry A container in the shape of an inverted pyramid with a square base of \(2\textrm{ m}\) by \(2\textrm{ m}\) and height of \(5\textrm{ m}\) is filled to a depth of \(4\textrm{ m}\) with corn slurry. How much work is required to pump all the slurry over the top of the container? (The density of corn slurry is \(\rho =17.9\textrm{ kg/m}^{3}\).)

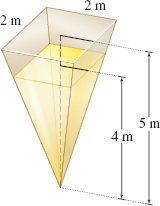
Question

Pumping Olive Oil from a Vat A vat in the shape of an inverted pyramid with a rectangular base that measures \(2\textrm{ m}\) by \(0.5\textrm{ m}\) and height that measures \(4\textrm{ m}\) is filled to a depth of \(2\textrm{ m}\) with olive oil. How much work is required to pump all the olive oil over the top of the vat? (The density of olive oil is \(\rho =0.9\textrm {/cm}^{3}\).)

Question

Work to Lift an Elevator How much work is required if six cables, each weighing \(0.36\textrm{ lb/in}\)., lift a 10,000-lb elevator 400 ft? Assume the cables work together and equally share the weight of the elevator.

Question

Work by Gravity A cable with a uniform linear mass density of \(9\textrm{ kg/m}\) is being unwound from a cylindrical drum. If \(15\textrm{ m}\) are already unwound, what is the work done by gravity in unwinding another \(60\textrm{ m}\) of the cable?

Question

Work to Lift a Bucket and Chain A uniform chain \(10\textrm{ m}\) long and with mass \(20\textrm{ kg}\) is hanging from the top of a building \(10\textrm{ m}\) high. If a bucket filled with cement of mass \(75\textrm{ kg}\) is attached to the end of the chain, how much work is required to pull the bucket and chain to the top of the building?

Question

Work to Lift a Bucket and Chain In Problem 23, if a uniform chain \(10\textrm{ m}\) long and with mass \(15\textrm{ kg}\) is used instead, how much work is required to pull the bucket and chain to the top of the building?

Question

Work of a Spring A spring, whose equilibrium length is \(1 {m}\), extends to a length of \(3\textrm{ m}\) when a force of \(3\textrm{ N}\) is applied. Find the work needed to extend the spring to a length of \(2\textrm{ m}\) from its equilibrium length.

Question

Work of a Spring A spring, whose equilibrium length is \(2 \textrm{ m}\), is compressed to a length of \(\dfrac{1}{2}\textrm{ m}\) when a force of \(10\textrm{ N}\) is applied. Find the work required to compress the spring to a length of \(1\textrm{ m}\).

Question

Work of a Spring A spring, whose equilibrium length is \(4 \textrm {ft}\), extends to a length of \(8\textrm {ft}\) when a force of \(2~\textrm {lb}\) is applied. If \(9~\textrm {ft-lb}\) of work is required to extend this spring from its equilibrium position, what is its total length?

Question

Work of a Spring If \(8\textrm {ft-lb}\) of work is used on the spring in Problem 27, how far is it extended?

452

Question

Work to Pump Water A full water tank in the shape of an inverted right circular cone is \(8\textrm {m}\) across the top and \(4\textrm {m}\) high. How much work is required to pump all the water over the top of the tank? (The density of water is \(1000\textrm {kg/m}^{3}\).)

Question

Work to Pump Water If the surface of the water in the tank of Problem 29 is \(2\textrm{ m}\) below the top of the tank, how much work is required to pump all the water over the top of the tank?

Question

Work to Pump Water A water tank in the shape of a hemispherical bowl of radius \(4\textrm{ m}\) is filled with water to a depth of \(2\textrm{ m}\). How much work is required to pump all the water over the top of the tank?

Question

Work to Pump Water If the water tank in Problem 31 is completely filled with water, how much work is required to pump all the water to a height \(2\textrm {m}\) above the tank?

Question

Work to Pump Water A cylindrical tank, \(4\textrm {m}\) in diameter and \(6\textrm {m}\) high, is full of water. How much work is required to pump half the water over the top of the tank? (The density of water is \(1000\textrm {kg/m}^{3}\).)

Question

Work to Pump Water A swimming pool is in the shape of a rectangular parallelepiped \(6\textrm {ft}\) deep, \(30\textrm {ft}\) long, and \(20\textrm {ft}\) wide. It is filled with water to a depth of \(5\textrm {ft}\). How much work is required to pump all the water over the top? (Hint: The weight of water is \(\rho g=62.42\textrm {lb/ft}^{3}\).)

Question

Work to Pump Water A 1 \(\textrm {hp}\) motor can do \(550\textrm {ft-lb}\) of work per second. The motor is used to pump the water out of a swimming pool in the shape of a rectangular parallelepiped \(5\textrm {ft}\) deep, \(25\textrm {ft}\) long, and \(15\textrm {ft}\) wide. How long does it take for the pump to empty the pool if the pool is filled to a depth of \(4\textrm {ft}\)? (The weight of water is \(62.42~\textrm {lb/ft}^{3}\).)

Question

The minimum energy required to move an object of mass \(30~\textrm {kg}\) a distance \(30~\textrm {km}\) above the surface of Earth is equal to the work required to accomplish this. Find the work required. (Earth's radius \(R\) is approximately \(6370\textrm {km}\).)

Question

The minimum energy required to move a rocket of mass \(1000~\textrm {kg}\) a distance of \(800~\textrm {km}\) above Earth's surface is equal to the work required to do this. Find the work required.

Question

Coulomb's Law By Coulomb's Law, a positive charge \(m\) of electricity repels a unit of positive charge at a distance \(x\) with the force \(\dfrac{m}{x^{2}}\). What is the work done when the unit charge is carried from \(x=2a\) to \(x=a\), \(a>0\)?

Question

Work to Lift a Leaky Load In raising a leaky bucket from the bottom of a well \(25\textrm {ft}\) deep, one-fourth of the water is lost. If the bucket weighs \(1.5\textrm {lb}\), the water in the bucket at the start weighs \(20\textrm {lb}\), and the amount that has leaked out is assumed to be proportional to the distance the bucket is lifted, find the work done in raising the bucket. Ignore the weight of the rope used to lift the bucket.

Question

Work of a Spring The spring constant on a bumping post in a freight yard is \(300{,}000\textrm {N/m}\). Find the work done in compressing the spring \(0.1\textrm {m}\).

Question

Work to Pump Water A container is formed by revolving the region bounded by the graph of \(y=x^{2}\), and the \(x\)-axis, \(0\leq x\leq 2\), about the \(y\)-axis. How much work is required to fill the container with water from a source \(2\) units below the \(x\)-axis by pumping through a hole in the bottom of the container?

Question

Work of a Spring The force in newtons required to stretch a spring \(x\textrm {meters}\) beyond its equilibrium length is given by \(F(x) =-100x\).

1. What force will stretch the spring \(0.1\textrm {m}\)? \(0.2\textrm {m}\)? \(0.4\textrm {m}\)?
2. How much work is required to stretch the spring \(0.1\textrm {m}\)? \(0.2\textrm {m}\)? \(0.4\textrm {m}\)?

source: Adapted from F.W.Sears, M.W.Zemansky, & H.D.Young (1976), (University physics) (p. 132), Reading, MA: Addison-Wesley. Reprinted by permission.

Question

Work to Pump Heating Oil A cylindrical tank \(6\) m long and 4~m in diameter is lying on its side and is half full of heating oil. (The density of heating oil is \(820 \textrm {kg/m}^{3}.)\)

1. Set up an integral to find the work done in pumping the oil over the top of the tank. Choose \(x=0\) for the position of the base of the tank.
2. Find the work done in pumping the oil over the top of the tank to the nearest joule.

Question

Work to Move a Piston The force exerted by a gas in a cylinder on a piston whose area is \(A\), is given by \(F=pA\), where \(p\) is the force per unit area, or pressure. The work \(W\) in displacing the piston from \(x_{1}\) to \(x_{2}\) is \[ W=\int_{x_{1}}^{x_{2}}F~{\it dx}=\int_{x_{1}}^{x_{2}}pA~{\it dx}=\int_{V_{1}}^{V_{2}}p~dV \]

where \(dV\) is the accompanying infinitesimal change of volume of the gas.

1. During expansion of a gas at constant temperature (isothermal), the pressure depends on the volume according to the relation

   \[ p=\frac{nRT}{V} \]

   where \(n\) and \(R\) are constants and \(T\) is the constant temperature. Calculate the work in expanding the gas isothermally from volume \(V_{1}\) to volume \(V_{2}\).

2. During expansion of a gas at constant entropy (adiabatic), the pressure depends on the volume according to the relation

   \[ p=\frac{K}{V^{\gamma }} \]

   where \(K\) and \(\gamma \neq 1\) are constants. Calculate the work in expanding the gas adiabatically from \(V_{1}\) to \(V_{2}\).

Question

Work of Expanding Gas The pressure of \(1\textrm{ lb}\) of a gas is \(100\textrm{ lb} \textrm{\in}^{2}\) and the volume is \(2\textrm{ ft}^{3}\). Find the work done by the gas in expanding to double its volume according to the law \(pV^{1.4}=c\) (in pounds per cubic foot).

Question

Work of Expanding Gas The pressure and volume of a certain gas obey the law \(pV^{1.2}=120\) (in inch-pounds). Find the work done when the gas expands from \(V=2.4\) to \(V=4.6\textrm{ in}^{3}\).