6.7 Hydrostatic Pressure and Force
NOTE
Fluids are substances that can flow. Gases and liquids are fluids.
OBJECTIVE
When you finish this section, you should be able to:
- Find hydrostatic pressure and force (p. 453)
IN WORDS
Pressure equals force per unit area.
When engineers design containers to hold fluids in place, it is important to know the pressure \(P\) caused by the force \(F\) of the fluid on the sides of the container. Pressure \(P\) is defined as the force \(F\) exerted per unit area \(A.\) \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ P=\dfrac{F}{A} } \end{equation*}
1 Find Hydrostatic Pressure and Force
Recall that the weight of a fluid is given by the formula \(F=\rho gV,\) where \(\rho\) is the mass density of the fluid, \(g\approx 9.8 \textrm {m/s}^{2}\approx 32.2 \textrm {ft/s}^{2}\) is the acceleration due to gravity, and \(V\) is the volume of the fluid. Then, at a depth \(h\) below the surface of the fluid, the pressure \(P\) is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ P=\dfrac{\rho gV}{A}=\rho gh } \end{equation*}
As the formula indicates, the pressure \(P\) is directly proportional to the depth \(h\), so the pressure increases as the depth increases.
\(P\) is often called hydrostatic pressure, and the force \(F\) a hydrostatic force, because they are the result of fluids, such as water (hydro), that are at rest (static). Table 2 summarizes the units of measure used for these calculations.
| Pressure, \(P\) | Mass Density, \(\rho\) | \(g\) | Depth, \(h\) | |
|---|---|---|---|---|
| SI | Pascal \((\textrm{Pa}) = \textrm{newton/meter}^2~(\textrm{Pa} = \textrm{N/m}^2\)) | \(\textrm{kilogram/meter}^3 (\textrm {kg/m}^{3}\)) | \(9.8\textrm {m/s}^{2}\) | \(\textrm{meter} (\textrm {m}\)) |
| U.S. | \(\textrm{pound/foot}^2~(\textrm {lb/ft}^2\)) | \(\textrm{slug/foot}^3~(\textrm {slug/ft}^3\)) | \(32.2\textrm {ft/s}^{2}\) | \(\textrm{foot} (\textrm {ft}\)) |
When using U.S. units, the weight density \(\rho g\) measured in pounds per square foot is often used (and the unit slug is not apparent). Then pressure \(P\) is written \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ P=\hbox{(Weight density)(Depth) }\textrm {lb}/{\!ft}^{2} } \end{equation*}
As an example, suppose a thin, flat plate of area \(A\) is suspended horizontally in water at a depth \(h\). The force \(F\) of the water on the bottom face of the plate equals the weight of the water above the plate. \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ F=\rho gV=\rho ghA } \end{equation*}
454
The weight density of water is about \(62.5\textrm{ lb/ft}^{3}\), so if the plate were suspended horizontally at a depth of \(4\textrm{ ft}\), the weight of the water on the plate is \begin{equation*} F=\rho ghA=( 62.5) ( 4) A=250A\textrm{ lb} \end{equation*}
and the pressure of the water on the plate is \begin{equation*} P=\dfrac{F}{A}=250\textrm{ lb/ft}^{2} \end{equation*}
If the plate has an area of \(2\textrm{ ft}^{2}\), the force \(F\) of the water exerted on one side of the plate is \(F=AP=(2)(250)=500\textrm{ lb}\). In fact, as the horizontal plate at a depth \(h\) changes in size and or shape, the hydrostatic force \(F\) varies, but the hydrostatic pressure \(P\) remains constant. Nevertheless, the deeper the plate is in the fluid, the greater the pressure is on the plate.
IN WORDS
The pressure \(P\) due to a static fluid on a horizontal plate depends on the depth of the plate in the fluid.
If a plate is suspended vertically in a fluid, the pressure at the bottom of the plate is greater than the pressure at the top. To find the force of the fluid on one side of the plate, suppose the plate is suspended vertically in a fluid of mass density \(\rho\). Suppose further that the plate is placed in a rectangular coordinate system and is enclosed by \(y=c\), \(y=d\), \(x=g(y)\), and \(x=f(y)\), where \(f\) and \(g\) are functions that are continuous on the closed interval \([c,d]\) and \(f(y)\geq g(y)\) for all numbers \(y\) in \([c,d].\) See Figure 61.
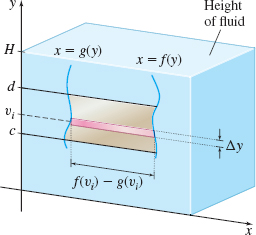
The surface of the fluid is the line \(y=H\), where \(H\geq d\), so that the top of the plate is at a depth of \((H-d)\) and the bottom of the plate is at a depth of \((H-c)\).
Partition the interval \([c,d]\) into \(n\) subintervals: \begin{equation*} [ c, y_{1}] , [ y_{1}, y_{2}] , \ldots , [y_{i-1}, y_{i}] , \ldots , [ y_{n-1}, d] \qquad c=y_{0}\quad d=y_{n} \end{equation*} each of length \(\Delta y=\dfrac{d-c}{n}\), and let \(v_{i}\) be a number in the \(i\)th subinterval \([ y_{i-1},y_{i}] ,\) \(i=1,2,3,\ldots , n\). If the length \(\Delta y\) is small, then all points in the horizontal \(i\)th slice of the plate are roughly the same distance \((H-v_{i})\) from the surface, and the pressure \(P_{i}\) of the fluid on this portion of the plate is approximately \(P_{i}=\rho g(H-v_{i})\). The force \(F_{i}\) due to hydrostatic pressure on the \(i\)th subinterval of the plate is approximately \[ F_{i}=\rho ghA_{i}\approx \rho g(H-v_{i})[f(v_{i})-g(v_{i})]\Delta y \qquad {\color{#0066A7}{A_{i} = [ f (v_{i} ) - g ( v_{i} ) ] \Delta y}} \]
An approximation to the total force \(F\) on the plate can be found by summing the forces from each subinterval. That is, \begin{equation*} F\approx \sum_{i=1}^{n}\underset{\color{#0066A7}{\hbox{Weight density of slice }}}{\underbrace{\rho g}}\underset{\color{#0066A7}{\hbox{Depth of slice}}}{\underbrace{(H-v_{i})}}\underset{\color{#0066A7}{\hbox{ Area of the slice}}}{\underbrace{[ f(v_{i})-g(v_{i})] ~\Delta y}} \end{equation*}
As the number of subintervals increases, that is, as \(n\rightarrow \infty\), the sums \(F\) become better approximations of the force due to fluid pressure on the plate. Since these are Riemann sums and the functions \(f\) and \(g\) are continuous on \([c,d]\), the limit is a definite integral. That is, \begin{equation*} F=\lim\limits_{n\rightarrow \infty }\sum_{i=1}^{n}\rho g(H-v_{i})[ f(v_{i})-g(v_{i})] \Delta y=\displaystyle \int_{c}^{d}\rho g( H-y) [ f(y)-g(y)] ~{\it dy} \end{equation*}
Hydrostatic Force
The hydrostatic force \(F\) due to the pressure exerted by a fluid of mass density \(\rho\) on a plate of the type illustrated in Figure 61, where the functions \(f\) and \(g\) are continuous on the closed interval \([c,d]\), is \begin{align*} \bbox[5px, border:1px solid black, #F9F7ED]{ F=\displaystyle \int_{c}^{d}\rho g( H-y) [ f(y)-g(y)] ~{\it dy} } \end{align*}
455

Finding Hydrostatic Force
A trough, whose cross section is a trapezoid, measures 2 m across at the bottom and 4 m across at the top, and is 2 m deep. If the trough is filled with a liquid of mass density \(\rho\), what is the force due to hydrostatic pressure on one end of the trough?
Solution We position the trough in a rectangular coordinate system, as shown in Figure 62.
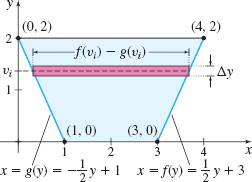
The sides of the end of the trough are lines that pass through the points \( (0,2),\) \((1,0)\) and the points \((3,0),\) \((4,2)\), respectively. The equations of these lines are \begin{equation*} y-2=\dfrac{0-2}{1-0}(x-0)=-2x\qquad\hbox{or equivalently}\qquad x=g(y)=-\dfrac{1}{2}y+1 \end{equation*}
and \begin{equation*} y-0=\dfrac{2-0}{4-3}(x-3)=2x-6\qquad\hbox{or equivalently}\qquad x=f(y)=\dfrac{1}{2}y+3 \end{equation*}
Then the hydrostatic force on the \(i\)th interval of the trough is \begin{equation*} F_{i}=\,\underset{\color{#0066A7}{\hbox{Weight}}}{\underbrace{\rho \cdot g\,}}\underset{\color{#0066A7}{\hbox{ Depth}}}{\underbrace{( H-v_{i}) }\,}\underset{\color{#0066A7}{\hbox{Area}}}{ \underbrace{[ f( v_{i}) -g( v_{i}) ] \Delta y}}\underset{\color{#0066A7}{\hbox{$H=2$}}}{\underset{\color{#0066A7}{\uparrow }}{=}}\rho g( 2-v_{i}) [ f( v_{i}) -g( v_{i}) ] \Delta y \end{equation*}
The liquid fills the trough from \(y=0\) to \(y=2,\) so the hydrostatic force \(F\) due to the pressure of the liquid on an end of the trough is \begin{eqnarray*} F &=&\int_{0}^{2}\rho g(2-y)[f(y)-g(y)] ~{\it dy}\\[5pt] &=&\int_{0}^{2}\rho g(2-y)\left[ \left( \dfrac{1}{2}y+3\right) -\left( -\dfrac{1}{2}y+1\right) \right] {\it dy}=\rho g\int_{0}^{2}(2-y)(y+2)~{\it dy} \notag \\[5pt] &=&\rho g\int_{0}^{2}(-y^{2}+4)~{\it dy}=\rho g\left[ -\dfrac{y^{3}}{3}+4y\right] _{0}^{2}=\rho g\!\left( -\dfrac{8}{3}+8\right) =\dfrac{16}{3}\rho g\hbox{ } \textrm{ N} \end{eqnarray*}
NOW WORK
Problem 13.
So far we have positioned the coordinate system so that the submerged plate is located in the first quadrant. As the next example illustrates, the coordinates may be placed in any convenient position. Keep in mind that the essential idea behind the formula for force due to hydrostatic pressure is \begin{equation*} \hbox{Hydrostatic force}=\rho g\times \hbox{Depth}\times \hbox{Area} \end{equation*}
456
Finding Hydrostatic Force
A cylindrical sewer pipe of radius 2 m is half full of water. A gate used to seal off the sewer is placed perpendicular to the pipe opening. Find the hydrostatic force exerted on one side of the gate.
Solution We position a cross section of the pipe (a circle) so its center is at the origin. See Figure 63.
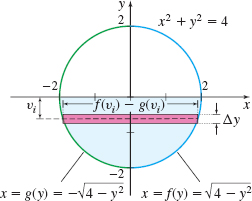
The equation of the circle with center at \((0,0)\) and radius \(2\) is \(x^{2}+y^{2}=4\). Then \[ x=g(y)=-\sqrt{4-y^{2}}\qquad \hbox{and }\qquad x=f(y)=\sqrt{4-y^{2}} \]
The height of the water is at \(H=0\). Since the water fills the cylinder from \(y=-2\) to \(y=0,\) the hydrostatic force \(F\) exerted on one side of the gate by the pressure of the water is \[ \begin{array}{rcl@{\qquad}l} F &=&\int_{c}^{d}\rho g( {H-y}) [ f(y)-g(y)] ~{\it dy} & \\[3pt] &=&\int_{-2}^{0}\rho g(0-y)\big[ \sqrt{4-y^{2}}-\big( -\!\sqrt{4-y^{2}}\big) \big] ~{\it dy} &\color{#0066A7}{H=0; c=-2; d=0.} \\ &=&9800\int_{-2}^{0}-2y\sqrt{4-y^{2}}~{\it dy} &\color{#0066A7}{\rho =1000\hbox{ kg}/\hbox{m}^{3}; g=9.8\ \hbox{ m}/\hbox{s}^{2}.} \\ &=&9800\int_{0}^{4}\sqrt{u}~{\it du}=9800\left[ \frac{2u^{3/2}}{3}\right]_{0}^{4} &\color{#0066A7}{\hbox{Let \(u=4-y^{2} \); }} \\ &&&\color{#0066A7}{\hbox{then \(du=-2y~{dy} \).}}\\ &&&\color{#0066A7}{\hbox{When \(y=-2 \), then \(u=0 \);}} \\ &&&\color{#0066A7}{\hbox{when \(y=0 \), then \(u=4 \).}}\\[-3pc] \\ &=&9800\left( \dfrac{16}{3}\right) \approx 52{,}267 {N} \end{array}\]
NOW WORK
Problem 15.