6.1 Assess Your Understanding
Concepts and Vocabulary
Question
Express the area between the graphs of \(y=x^{2}\) and \(y=\sqrt{x}\) as an integral using a partition of the \(x\)-axis. Do not find the integral.
Question
Express the area between the graph of \(x=y^{2}\) and the line \(x=1\) as an integral using a partition of the \(y\)-axis. Do not find the integral.
Skill Building
In Problems 3–12, find the area of the region enclosed by the graphs of the given equations by partitioning the \(x\)-axis.
Question
\(y = x, y =2x, x=1\)
Question
\(y = x, y =3x, x=3\)
Question
\(y=x^{2}, y=x\)
Question
\(y=x^{2}, y=4x\)
Question
\(y =e^{x}, y =e^{-x}, x=\ln 2\)
Question
\(y =e^{x}, y =-x+1, x=1\)
Question
\(y=x^{2}, y=x^{4}\)
Question
\(y=x, y=x^{3}\)
Question
\(y=\cos x, y=\dfrac{1}{2}, 0\leq x\leq \dfrac{\pi}{3}\)
Question
\(y=\sin x, \ y=\dfrac{1}{2}, \dfrac{\pi}{6}\leq x\leq \dfrac{5\pi}{6}\)
In Problems 13–20, find the area of the region enclosed by the graphs of the given equations by partitioning the \(y\)-axis.
Question
\(x=y^{2}, x=2-y\)
Question
\(x=y^{2}, x=y+2\)
Question
\(x=9-y^{2}, x=5\)
Question
\(x=16-y^{2}, x=7\)
Question
\(x=y^{2}+4, y=x-6\)
Question
\(x=y^{2}+6, y=8-x\)
Question
\(y=\ln x, x=1, y=2\)
Question
\(y=\ln x, x=e, y=0\)
In Problems 21–24, find the area of the shaded region in the graph.
Question
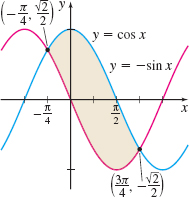
Question

Question
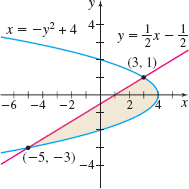
Question
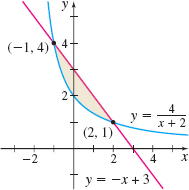
In Problems 25–32, find the area \(A\) of the region enclosed by the graphs of the given equations:
- by partitioning the \(x\)-axis.
- by partitioning the \(y\)-axis.
Question
\(y=\sqrt{x}, y=x^{3}\)
Question
\(y=\sqrt{x}, y=x^{2}\)
Question
\(y=x^{2}+1, y=x+1\)
Question
\(y=x^{2}+1, y=4x+1\)
412
Question
\(y=\sqrt{9-x}, y=\sqrt{9-3x}, x\)-axis
Question
\(y=\sqrt{16-2x}, y=\sqrt{16-4x}, x\)-axis
Question
\(y=\sqrt{2x-6}, y=\sqrt{x-2}, x\)-axis
Question
\(y=\sqrt{2x-5}, y=\sqrt{4x-17}, x\)-axis
In Problems 33–46, find the area of the region enclosed by the graphs of the given equations.
Question
\(y=4-x^{2}, y=x^{2}\)
Question
\(y=9-x^{2}, y=x^{2}\)
Question
\(x=y^{2}-4, x=4-y^{2}\)
Question
\(x=y^{2}, x=16-y^{2}\)
Question
\(y=\ln x^{2}\), the \(x\)-axis, and the line \(x=e\)
Question
\(y=\ln x, y=1-x\), and the line \(y=1\)
Question
\(y=\cos x, y=1-\dfrac{3}{\pi}x, x=\dfrac{\pi}{3}\)
Question
\(y=\sin x, y=1, 0\leq x\leq \dfrac{\pi}{2}\)
Question
\(y=e^{2x}\) and the lines \(x=1\) and \(y=1\)
Question
\(y=e^{x}, y=e^{3x}, x=2\)
Question
\(y^{2}=4x, 4x-3y-4=0\)
Question
\(y^{2}=4x+1, x=y+1\)
Question
\(y=\sin x, y=\dfrac{2x}{\pi}, x\geq 0\)
Question
\(y=\cos x, x\geq 0, y=\dfrac{3x}{\pi}\)
Applications and Extensions
Question
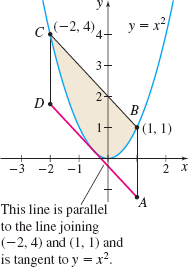
An Archimedean Result Show that the area of the shaded region in the figure is two-thirds of the area of the parallelogram ABCD. (This illustrates a result due to Archimedes concerning sectors of parabolas.)
Question
Equal Areas Find \(h\) so that the area of the region enclosed by the graphs of \(y=x, y=8x\), and \(y=\dfrac{1}{x^{2}}\) is equal to that of an isosceles triangle of base \(1\) and height \(h\). See the figure.

Question
Cost of Health Care The cost of health care varies from one country to another. Between 2000 and 2010, the average cost of health insurance for a family of four in the United States was modeled by \begin{equation*} A(x) =8020.6596( 1.0855^{x})\qquad 0\leq x\leq 10 \end{equation*}
where \(x=0\) corresponds to the year 2000 and \(A(x)\) is measured in U.S. dollars. During the same years, the average cost of health care in Canada was given by \begin{equation*} C(x) =4944.6424( 1.0711^{x}) \qquad 0\leq x\leq 10 \end{equation*}
where \(x=0\) corresponds to the year 2000 and \(C(x)\) is measured in U.S. dollars.
- Find the area between the graphs from \(x=0\) to \(x=10\). Round the answer to the nearest dollar.
- Interpret the answer to (a).
Question
Area Find the area in the first quadrant enclosed by the graphs of \(y=\sin (2x)\) and \(y=\cos (2x), 0\leq x\leq \dfrac{\pi}{8}\).
Question
Area Find the area of the region enclosed by the graphs of \(y=\sin ^{-1}x, y=x, 0\leq x\leq \dfrac{1}{2}\). Which axis did you choose to partition? Explain your choice.
Question
![]() Area
Area
- Graph \(y=x^{2}\) and \(y=\sin x\).
- Find the points of intersection of the graphs.
- Find the area enclosed by the graphs of \(y=x^{2}\) and \(y=\sin x\) using a partition of the \(x\)-axis.
- Find the area enclosed by the graphs of \(y=x^{2}\) and \(y=\sin x\) using a partition of the \(y\)-axis.
Question
![]()
- Graph \(y=\sin ^{-1}x, x+y=1\), and \(y=0\).
- Find the points of intersection of the graphs.
- Find the area enclosed by the graphs.
Question
![]()
- Graph \(y=\cos ^{-1}x, y=x^{3}+1\), and \(y=0\).
- Find the points of intersection of the graphs.
- Find the area enclosed by the graphs.
Question
![]()
- Graph \(2x+y=3, y=\dfrac{1}{1+x^{2}}\), and \(y=1\).
- Find the points of intersection of the graphs.
- Find the area enclosed by the graphs.
Question
![]()
- Graph \(y=\dfrac{5}{1+x^{2}}, x=\sqrt{y+2}\), and \(x=0\).
- Find the points of intersection of the graphs.
- Find the area enclosed by the graphs.
Question
![]()
- Graph \(y=\sin ^{-1}x, y=1-x^{2}\), and \(y=0\).
- Find the points of intersection of the graphs.
- Find the area enclosed by the graphs.
Challenge Problems
Question
Find the area enclosed by the graph of \(y^{2}=x^{2}-x^{4}\).
Question
- Express the area \(A\) of the region in the first quadrant enclosed by the \(y\)-axis and the graphs of \(y=\tan x\) and \(y=k\) for \(k>0\) as a function of \(k\).
413
- What is the value of \(A\) when \(k=1\)?
- If the line \(y=k\) is moving upward at the rate of \(\dfrac{1}{10}\) unit per second, at what rate is \(A\) changing when \(k=1\)?
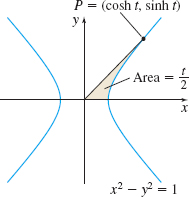
Question
The area \(A\) of the shaded region in the figure is \(A = \dfrac{t}{2}\). Prove this as follows:
- Let \(A^{\ast}\) be twice the area outlined in the figure, and \((x,y)\) be the coordinates of \(P\). Explain why \begin{equation*} A^{\ast }=x\sqrt{x^{2}-1}-2\int_{1}^{x}\sqrt{u^{2}-1}\,{\it du} \end{equation*}
- Differentiate \(A^*\) to show that \(\dfrac{dA^{\ast }}{{\it dx}}=\dfrac{1}{\sqrt{x^{2}-1}}\).
- Show that \(A^{\ast }=\cosh ^{-1}x+C\), and explain why \(C=0\).
- Why does it follow that \(A^{\ast }=t\)?