6.2 Assess Your Understanding
Concepts and Vocabulary
Question
If a function \(f\) is continuous on a closed interval \([a,b]\), then the volume \(V\) of the solid of revolution obtained by revolving the region bounded by the graph of \(f\), the \(x\)-axis, and the lines \(x = a\) and \(x = b\) about the \(x\)-axis, is found using the formula \(V =\)_____.
Question
True or False When the region bounded by the graphs of the functions \(f\) and \(g\) and the lines \(x=a\) and \(x=b\) is revolved about the \(x\)-axis, the cross section exposed by making a slice at \(u_i\) perpendicular to the \(x\)-axis is two concentric circles, and the area \(A_{i}\) between the circles is \(A_{i}=\pi [f(u_{i})-g(u_{i})]^{2}\).
Question
True or False If the functions \(f\) and \(g\) are continuous on the closed interval \([a,b]\) and if \(f(x) \geq g(x) \geq 0\) on the interval, then the volume \(V\) of the solid of revolution obtained by revolving the region bounded by the graphs of \(f\) and \(g\) and the lines \(x = a\) and \(x = b\) about the \(x\)-axis is \(V=\pi \int^b_a [f(x) - g(x)]^2~{\it dx}\).
Question
True or False If the region bounded by the graphs of \(y=x^{2}\) and \(y=2x\) is revolved about the line \(y=6\), the volume \(V\) of the solid of revolution generated is found by finding the integral \[ V=\pi \int_{6}^{7}( 4x^2-x^{4})\, {\it dx}. \]
Skill Building
In Problems 5–10, find the volume of the solid of revolution generated by revolving the region shown below about the indicated axis.
Question
\(y=2\sqrt{x}\) about the \(x\)-axis
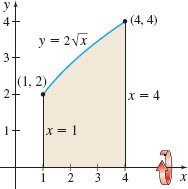
Question
\(y=x^{4}\) about the \(y\)-axis

423
Question
\(y=\dfrac{1}{x}\) about the \(y\)-axis
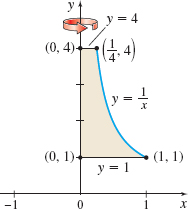
Question
\(y=x^{2/3}\) about the \(y\)-axis
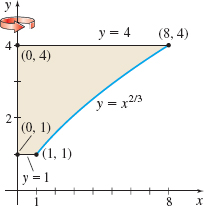
Question
\(y=\sec x\) about the \(x\)-axis

Question
\(y=x^{2}\) about the \(y\)-axis
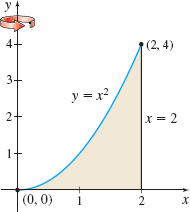
In Problems 11–16, use the disk method to find the volume of the solid of revolution generated by revolving the region bounded by the graphs of the given equations about the indicated axis.
Question
\(y=2x^{2}\), the \(x\)-axis, \(x=1\); about the \(x\)-axis
Question
\(y=\sqrt{x}\), the \(x\)-axis, \(x=4, x=9\); about the \(x\)-axis
Question
\(y=e^{-x}\), the \(x\)-axis, \(x=0, x=2\); about the \(x\)-axis
Question
\(y=e^{x}\), the \(x\)-axis, \(x=-1, x=1\); about the \(x\)-axis
Question
\(y=x^{2}, x\geq 0, y=1, y=4\); about the \(y\)-axis
Question
\(y=2\sqrt{x}\), the \(y\)-axis, \(y=4\); about the \(y\)-axis
In Problems 17–22, use the washer method to find the volume of the solid of revolution generated by revolving the region bounded by the graphs of the given equations about the indicated axis.
Question
\(y=x^{2}, x\geq 0\), the \(y\)-axis, \(y=4\); about the \(x\)-axis
Question
\(y=2x^{2}, x\geq 0\), the \(y\)-axis, \(y=2\); about the \(x\)-axis
Question
\(y=2\sqrt{x}\), the \(y\)-axis, \(y=4\); about the \(x\)-axis
Question
\(y=x^{2/3}\), the \(x\)-axis, \(x=8\); about the \(y\)-axis
Question
\(y=x^{3}\), the \(x\)-axis, \(x=2\); about the \(y\)-axis
Question
\(y=2x^{4}\), the \(x\)-axis, \(x=1\); about the \(y\)-axis
In Problems 23–38, find the volume of the solid of revolution generated by revolving the region bounded by the graphs of the given equations about the indicated axis.
Question
\(y=\dfrac{1}{x}\), the \(x\)-axis, \(x=1, \ x=2\); about the \(x\)-axis
Question
\(y=\dfrac{1}{x}\), the \(x\)-axis, \(x=1, \ x=2\); about the \(y\)-axis
Question
\(y=\sqrt{x}\), the \(y\)-axis, \(y=9\); about the \(y\)-axis
Question
\(y=\sqrt{x}\), the \(y\)-axis, \(y=9\); about the \(x\)-axis
Question
\(y=(x-2) ^{3}\), the \(x\)-axis, \(x=0, x=3\); about the \(x\)-axis
Question
\(y=(x-2) ^{3}\), the \(x\)-axis, \(x=0, x=3\); about the \(y\)-axis
Question
\(y=(x+1) ^{2}, x\geq 0, y=16\); about the \(y\)-axis
Question
\(y=(x+1) ^{2}, x\leq 0, y=16\); about the \(x\)-axis
Question
\(x=y^{4}-1\), the \(y\)-axis; about the \(y\)-axis
Question
\(y=x^{4}-1\), the \(x\)-axis; about the \(x\)-axis
Question
\(y=4x, \ y=x^{3}, x\geq 0;\) about the \(x\)-axis
Question
\(y=2x+1, y=x, x=0, x=3;\) about the \(x\)-axis
Question
\(y=1-x, y=e^{x}, x=1\); about the \(x\)-axis
Question
\(y=\cos x, y=\sin x, x=0, x=\dfrac{\pi}{4};\) about the \(x\)-axis
Question
\(y=\csc x, y=0, x= \dfrac{\pi}{2}, x=\dfrac{3\pi }{4};\) about the \(x\)-axis
Question
\(y=\sec x, y=0, x=0, x=\dfrac{\pi}{3}\); about the \(x\)-axis
In Problems 39–46, find the volume of the solid of revolution generated by revolving the region bounded by the graphs of the given equations about the indicated line.
Question
\(y=e^{x}, y=0, x=0, x=2\); about \(y=-1\)
Question
\(y=\dfrac{1}{x}, y=0, x=1, x=4\); about \(y=4\)
Question
\(y=x^{2}\), the \(x\)-axis, \(x=1\); about \(x=1\)
Question
\(y=x^{3}, x=0, y=1\); about \(x=-1\)
Question
\(y=\sqrt{x}\), the \(x\)-axis, \(x=4\); about \(x=-4\)
Question
\(y=\dfrac{1}{\sqrt{x}}\), the \(x\)-axis, \(x=1, x=4\); about \(x=4\)
Question
\(y=\dfrac{1}{x^{2}}, y=0, x=1, x=4\); about \(y=4\)
Question
\(y=\sqrt{x}, y=0, 0\leq x\leq 4\); about \(y=-4\)
Applications and Extensions
Question
Volume of a Solid of Revolution A region in the first quadrant is bounded by the \(x\)-axis and the graph of \(y=kx-x^{2}\), where \(k > 0\).
- In terms of \(k\), find the volume generated when the region is revolved around the \(x\)-axis.
- In terms of \(k\), find the volume generated when the region is revolved around the \(y\)-axis.
- Find the number \(k\) for which the volumes found in parts (a) and (b) are equal.
Question
Volume of a Solid of Revolution
- Find all numbers \(b\) for which the graphs of \(y=2x+b\) and \(y^{2}=4x\) intersect in two distinct points.
- If \(b=-4\), find the area enclosed by the graphs of \(y=2x-4\) and \(y^{2}=4x\).
424
- If \(b=0\), find the volume of the solid generated by revolving about the \(x\)-axis the region bounded by the graphs of \(y=2x\) and \(y^{2}=4x\).
Question
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graphs of \(y=\cos x\) and \(y=0\) from \(x=0\) to \(x=\dfrac{\pi}{2}\) about the line \(y=1\). \(\left[ \hbox{Hint: }\cos ^{2}x=\dfrac{1+\cos (2x) }{2}.\right]\)
Question
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graphs of \(y=\cos x\) and \(y=0\) from \(x=0\) to \(x=\dfrac{\pi}{2}\) about the line \(y=-1\). (See the hint in Problem 49.)
Challenge Problems
Question
Volume of a Solid of Revolution The graph of the function \(P(x)=kx^{2}\) is symmetric with respect to the \(y\)-axis and contains the points \((0,0)\) and \((b,e^{-b^{2}})\), where \(b > 0\).
- Find \(k\) and write an equation for \(P=P(x)\).
- The region bounded by \(P\), the \(y\)-axis, and the line \(y=e^{-b^{2}}\) is revolved about the \(y\)-axis to form a solid. Find its volume.
- For what number \(b\) is the volume of the solid in (b) a maximum? Justify your answer.
Question
Volume of a Solid of Revolution Find the volume of the solid generated by revolving the region bounded by the catenary \(y=a~\cosh \left( \dfrac{x}{a}\right) +b-a\), the \(x\)-axis, \(x=0\), and \(x=1\) about the \(x\)-axis, where \(a > 0\) and \(b \geq 0\). \(\bigg[\textit{Hint:} \cosh ^{2}~x=\dfrac{\cosh ( 2x) +1}{2}.\bigg]\)
