6.3 Assess Your Understanding
Concepts and Vocabulary
Question
True or False In using the shell method to find the volume of a solid revolved about the \(x\)-axis, the integration occurs with respect to \(x\).
Question
True or False The volume of a cylindrical shell of outer radius \(R\), inner radius \(r\), and height \(h\) is given by \(V=\pi r^{2}h\).
Question
True or False The volume of a solid of revolution can be found using either washers or cylindrical shells only if the region is revolved about the \(y\)-axis.
Question
True or False If \(y=f(x)\) is a function that is continuous and nonnegative on the closed interval \([a, b], a\geq 0\), then the volume \(V\) of the solid generated by revolving the region bounded by the graph of \(f\) and the \(x\)-axis from \(x=a\) to \(x=b\) about the \(y\)-axis is \(V=2\pi \int_{a}^{b}xf(x)~{\it dx}\).
Skill Building
In Problems 5–16, use the shell method to find the volume of the solid of revolution generated by revolving the region bounded by the graphs of the given equations about the indicated axis.
Question
\(y=x^{2}+1\), the \(x\)-axis, \(0\leq x\leq 1\); about the \(y\)-axis
Question
\(y=x^{3}, y=x^{2}\); about the \(y\)-axis
Question
\(y=\sqrt{x}, y=x^{2}\); about the \(y\)-axis
Question
\(y=\dfrac{1}{x}\), the \(x\)-axis, \(x=1, x=4\); about the \(y\)-axis
Question
\(y=x^{3}\), the \(y\)-axis, \(y=8\); about the \(x\)-axis
Question
\(y=\sqrt{x}\), the \(y\)-axis, \(y=2\); about the \(x\)-axis
Question
\(x=\sqrt{y}\), the \(y\)-axis, \(y=1\); about the \(x\)-axis
Question
\(x=4\sqrt{y}\), the \(y\)-axis, \(y=4\); about the \(x\)-axis
Question
\(y=x, y=x^{2}\); about the \(x\)-axis
Question
\(y=x, y=x^{3}\); in the first quadrant; about the \(x\)-axis
Question
\(y=e^{-x^{2}}\), and the \(x\)-axis, from \(x=0\) to \(x=2\); about the \(y\)-axis
Question
\(y=x^{3}+x\) and the \(x\)-axis, \(0\leq x\leq 1;\) about the \(y\)-axis
In Problems 17–22, use the shell method to find the volume of the solid of revolution generated by revolving the region bounded by the graphs of the given equations about the indicated line.
Question
\(y=x^{2}, y=4x-x^{2}\); about \(x=4\)
Question
\(y=x^{2}, y=4x-x^{2}\); about \(x=3\)
Question
\(y=x^{2}, y=0, x=1, x=2\); about \(x=1\)
Question
\(y=x^{2}, y=0, x=1, x=2\); about \(x=-2\)
Question
\(x=y-y^{2}\), the \(y\)-axis; about \(y=-1\)
Question
\(x=y-y^{2}\), the \(y\)-axis; about \(y=1\)
In Problems 23–26, use either the shell method or the disk/washer method to find the volume of the solid of revolution generated by revolving the shaded region in each graph:
- about the \(x\)-axis.
- about the \(y\)-axis.
- Explain why you chose the method you used.
Question
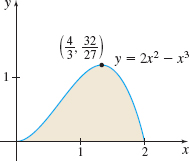
Question
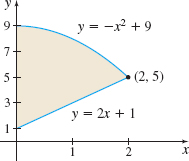
432
Question
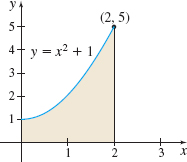
Question
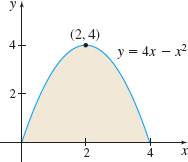
In Problems 27–38, use either the shell method or the disk/washer method to find the volume of the solid of revolution generated by revolving the region bounded by the graphs of the given equations about the indicated axis.
Question
\(y=\sqrt[3]{x}\), the \(y\)-axis, \(y=2\); about the \(x\)-axis
Question
\(y=\sqrt{x}+x\), the \(x\)-axis, \(x=1, x=4\); about the \(y\)-axis
Question
\(y=x^{3}\) and \(y=x\) to the right of \(x=0\); about the \(y\)-axis
Question
\(y=x^{3}, y=x^{2}\); about the \(x\)-axis
Question
\(y=3x^{2}\) and \(y=30-x\) to the right of \(x=1\); about the \(y\)-axis
Question
\(y=3x^{2}\) and \(y=30-x\) to the right of \(x=1\); about the \(x\)-axis
Question
\(y=x^{2}\) and \(y=8-x^{2}\) to the right of \(x=1\); about the \(x\)-axis
Question
\(y=x^{2}\) and \(y=8-x^{2}\) to the right of \(x=1\); about the \(y\)-axis
Question
\(y=x^{2}, y=x\); about the \(y\)-axis
Question
\(y=x^{2/3}+x^{1/3}\), the \(x\)-axis, \(x=1, x=8\); about the \(y\)-axis
Question
\(y=\sqrt{x}\) and \(y=18-x^{2}\) to the right of \(x=1\); about the \(y\)-axis
Question
\(y=\sqrt{x}\) and \(y=18-x^{2}\) to the right of \(x=1\); about the \(x\)-axis
Applications and Extensions
Question
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=\dfrac{1}{(x^2+1)^2}\) and the \(x\)-axis from \(x=0\) to \(x=1\) about the \(y\)-axis as shown in the figure.

Question
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=\sqrt{x+1}+x\) and the \(x\)-axis from \(x=0\) to \(x=3\) about the \(y\)-axis.
Question
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region in the first quadrant bounded by the \(x\)-axis and the graph of \(y=2x-x^{2}\):
- about the \(x\)-axis.
- about the \(y\)-axis.
- about the line \(x=3\).
- about the line \(y=1\).
Question
![]() Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region in the first quadrant bounded by the \(x\)-axis and the graph of \(y=x\sqrt{9-x}\).
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region in the first quadrant bounded by the \(x\)-axis and the graph of \(y=x\sqrt{9-x}\).
- about the \(x\)-axis.
- about the \(y\)-axis.
- about the line \(y=-3\).
- about the line \(x=-2\).
Question
Volume of a Solid of Revolution Suppose \(f(x)\geq 0\) for \(x\geq 0\), and the region bounded by the graph of \(f\) and the \(x\)-axis from \(x=0\) to \(x=k, k > 0\), is revolved about the \(x\)-axis. If the volume of the resulting solid is \(\dfrac{1}{5}k^{5}+k^{4}+\dfrac{4}{3}k^{3}\), find \(f\).
Question
Volume of a Solid of Revolution Find the volume of the solid generated by revolving about the \(y\)-axis the region bounded by the graph of \(y=e^{-x^{2}}\) and the \(y\)-axis from \(x=0\) to the positive \(x\)-coordinate of the point of inflection of \(y=e^{-x^{2}}\).
Question
![]() Volume of a Solid of Revolution Show that the volume \(V\) of the solid generated by revolving the region bounded by the graph of \(y=\sin ^{3}x\) and the \(x\)-axis from \(x=0\) to \(x=\pi\) about the line \(x=-\pi\) is given by \(V=4\pi^{2}\).
Volume of a Solid of Revolution Show that the volume \(V\) of the solid generated by revolving the region bounded by the graph of \(y=\sin ^{3}x\) and the \(x\)-axis from \(x=0\) to \(x=\pi\) about the line \(x=-\pi\) is given by \(V=4\pi^{2}\).
Challenge Problems
Question
Comparing Volume Formulas In the figure below, the region bounded by the graphs of \(y=g(x), y=f(x)\), and the \(y\)-axis is to be revolved about the \(y\)-axis. Show that the resulting volume \(V\) is given by:

- \(V=\pi a^{2}[f(a) -g(a)] +\,2\pi \displaystyle \int_{a}^{b}\!\!x[f(x)-g(x)]\, {\it dx}\) if the shell method is used.
- \(V=\pi \displaystyle \int_{g(a)}^{g(b)}[g^{-1}(y)]^{2}{\it dy}\,{+}\,\pi \int_{g(b)}^{f(a)} [f ^{-1}(y)] ^{2}{\it dy}\) if the disk method is used
Question
Suppose a plane region of area \(A\) that lies to the right of the \(y\)-axis is revolved about the \(y\)-axis, generating a solid of volume \(V\). If this same region is revolved about the line \(x=-k, k > 0\), show that the solid generated has volume \(V+2\pi kA\).
Question
Find the volume generated by revolving the region bounded by the parabola \(y^{2}=8x\) and its latus rectum about the latus rectum:
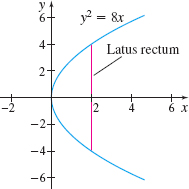
- by using the disk method.
- by using the shell method.
(The latus rectum is the chord through the focus perpendicular to the axis of the parabola.) See the figure.
