6.4 Assess Your Understanding
Concepts and Vocabulary
Question
In your own words, explain the method of slicing.
Question
True or False The slicing method works only with solids of revolution.
Skill Building
In Problems 3–12, find the volume of each solid by the method of slicing.
Question
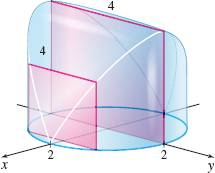
The base is a circle of radius 2; slices made perpendicular to the base are squares. See the figure.
Question
The base is a circle of radius \(2\); slices made perpendicular to the base are isosceles right triangles with one leg on the base.
Question
The solid is a pyramid 40 meters high whose horizontal cross section \(h\) meters from the top is a square with sides of length \(2h\) meters.
Question
The solid is a pyramid \(20\) meters high whose horizontal cross section \(h\) meters from the top is a rectangle with sides of length \(2h\) and \(h\) meters.
Question
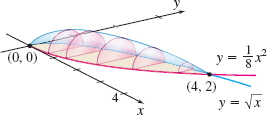
The base is enclosed by the graphs of \(y=\sqrt{x}\) and \(y=\dfrac{1}{8}x^2\); slices made perpendicular to the base along the \(x\)-axis have cross sections that are semi-circles. See the figure.
Question
The base is enclosed by the graphs of \(y=\sqrt{x}\) and \(y=\dfrac{1}{8}x^{2}\); slices made perpendicular to the base along the \(x\)-axis have cross sections that are triangles whose base is the distance between the graphs and whose height is 3 times the length of the base.
Question
The solid is horn-shaped; slices made perpendicular to the \(x\)-axis are circles whose diameters extend from the graph of \(y=x^{1/2}\) to the graph of \(y=\dfrac{4}{3}x^{1/3}\) from \(x=0\) to \(x=1\).
Question
The solid is horn-shaped; slices made perpendicular to the \( x \)-axis are circles whose diameters extend from the graph of \(y=x^{1/3}\) to \(y=\dfrac{3}{2}x^{1/3}\) from \(x=0\) to \(x=1\).
Question
The base is the area enclosed by \(y=x^{2}, x=1\), and \(y=0\); slices made perpendicular to the base along the \(x\)-axis are semicircles.
Question
The base is the area enclosed by the graphs of \(y=3\sqrt{3x}\) and \(y=x^{2}\); slices made perpendicular to the base along the \(x\)-axis are semicircles.
Applications and Extensions
Question
Verifying a Geometry Formula Use the slicing method to verify that the volume \(V\) of a sphere of radius \(R\) is \(V=\dfrac{4% }{3}\pi R^{3}.\)
Question
Volume of Water A hemispherical bowl of radius \(R\) contains water to the depth \(h\). Find the volume of the water in the bowl.
Question
Volume of Water Left in a Glass Suppose a cylindrical glass full of water is tipped until the water level bisects the base and touches the rim. What is the volume of the water remaining? Set up the integral; do not evaluate.
Question
Volume of a Wedge Suppose a wedge is cut from a solid right circular cylinder of diameter 10 m (like a wedge cut in a tree by an axe), where one side of the wedge is horizontal and the other is inclined at \(30^{\circ }\). See the figure below. If the horizontal part of the wedge penetrates 5 m into the cylinder and the two cuts meet along a vertical line through the center of the cylinder, find the volume of the wedge removed. (Hint: Vertical cross sections of the wedge are right triangles.)
438

Question
![]() Volume of a Solid Find the volume of the cylindrical solid with a bulge in the middle if slices taken perpendicular to the \(x\)-axis are circles whose diameters extend from the graph of \(y=e^{-x^{2}}\) to the graph of \(y=-e^{-x^{2}}\), \(-1\leq x\leq 1\).
Volume of a Solid Find the volume of the cylindrical solid with a bulge in the middle if slices taken perpendicular to the \(x\)-axis are circles whose diameters extend from the graph of \(y=e^{-x^{2}}\) to the graph of \(y=-e^{-x^{2}}\), \(-1\leq x\leq 1\).
Question
In your own words, explain why the disk method is a special case of the slicing method.
Challenge Problems
Question
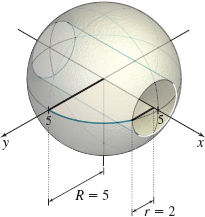
Volume of a Bore A hole of radius 2 centimeters is bored completely through a solid metal sphere of radius 5 cm. If the axis of the hole passes through the center of the sphere, find the volume of the metal removed by the drilling. See the figure.
Question
Volume The axes of two pipes of equal radii \(r\) intersect at right angles. Find their common volume.
Question
Volume of a Cone Find the volume of a cone with height \(h\) and an elliptical base whose major axis has length \(2a\) and minor axis has length \(2b\). (Hint: The area of this ellipse is \(\pi ab\).)
Question
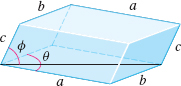
Volume of a Solid Find the volume of a parallelepiped with edge lengths \(a,b\), and \(c,\) where the edges having lengths \(a\) and \(b\) make an acute angle \(\theta \) with each other, and the edge of length \(c\) makes an acute angle of \(\phi \) with the diagonal of the parallelogram formed by \(a\) and \(b\).