Question

Multiple Choice A rational function \(R(x)=\frac{p(x)}{q(x)}\) is proper when the degree of \(p\) is [(a) less than, (b) equal to, (c) greater than] the degree of \(q.\)

Question

True or False Every improper rational function can be written as the sum of a polynomial and a proper rational function.

Question

True or False Sometimes the integration of a proper rational function leads to a logarithm.

Question

True or False The decomposition of \(\dfrac{7x+1}{(x+1) ^{4}}\) into partial fractions has three terms: \(\dfrac{A}{x+1}+\dfrac{B}{(x+1) ^{2}}+\dfrac{C}{(x+1) ^{3}},\) where \(A,\) \(B,\) and \(C\) are real numbers.

Question

\(\int \dfrac{x^{2}+1}{x+1}dx\)

Question

\(\int \dfrac{x^{2}+4}{x-2}dx\)

Question

\(\int \dfrac{x^{3}+3x-4}{x-2}dx \)

Question

\(\int \dfrac{x^{3}-3x^{2}+4}{x+3}dx\)

Question

\(\int \dfrac{dx}{(x-2)(x+1)}\)

Question

\(\int \dfrac{dx}{(x+4)(x-1)}\)

Question

\(\int \dfrac{x\,dx}{(x-1)(x-2)}\)

Question

\(\int \dfrac{3x\,dx}{(x+2)(x-4)}\)

Question

\(\int \dfrac{x\,dx}{(3x-2)(2x+1)}\)

Question

\(\int \dfrac{dx}{(2x+3)(4x-1)}\)

Question

\(\int \dfrac{x-3}{(x+2)(x+1)^{2}}\,dx\)

Question

\(\int \dfrac{x+1}{x^{2}(x-2)}\,dx\)

Question

\(\int \dfrac{x^{2}\,dx}{(x-1)^{2}(x+1)}\)

Question

\(\int \dfrac{x^{2}+x}{(x+2)(x-1)^{2}}\,dx \)

Question

\(\int \dfrac{dx}{x(x^{2}+1)}\)

Question

\(\int \dfrac{dx}{(x+1)(x^{2}+4)}\)

Question

\(\int \dfrac{x^{2}+2x+3}{(x+1)(x^{2}+2x+4)}dx\)

Question

\(\int \dfrac{x^{2}-11x-18}{x(x^{2}+3x+3)}dx\)

Question

\(\int \dfrac{2x+1}{(x^{2}+16)^{2}}dx\)

Question

\(\int \dfrac{x^{2}+2x+3}{(x^{2}+4)^{2}}dx \)

Question

\(\int \dfrac{x^{3}\,dx}{(x^{2}+16)^{3}}\)

Question

\(\int \dfrac{x^{2}\,dx}{(x^{2}+4)^{3}}\)

Question

\(\int \dfrac{x\,dx}{x^{2}+2x-3}\)

Question

\(\int \dfrac{x^{2}-x-8}{(x+1)(x^{2}+5x+6)}\,dx\)

Question

\(\int \dfrac{10x^{2}+2x}{(x-1)^{2}(x^{2}+2)}dx\)

Question

\(\int \dfrac{x+4}{x^{2}(x^{2}+4)}\,dx \)

Question

\(\int \dfrac{7x+3}{x^{3}-2x^{2}-3x}\,dx\)

Question

\(\int \dfrac{x^{5}+1}{x^{6}-x^{4}}\,dx\)

Question

\(\int \dfrac{x^{2}}{(x-2) (x-1) ^{2}}dx\)

Question

\(\int \dfrac{x^{2}+1}{(x+3) (x-1) ^{2}}\,dx\)

Question

\(\int \dfrac{2x+1}{x^{3}-1}dx\)

Question

\(\int \dfrac{dx}{x^{3}-8}\)

Question

\(\int_{0}^{1}\dfrac{dx}{x^{2}-9}\)

Question

\(\int_{2}^{4}\dfrac{dx}{x^{2}-25}\)

Question

\(\int_{-2}^{3}\dfrac{dx}{16-x^{2}}\)

Question

\(\int_{1}^{2}\dfrac{dx}{9-x^{2}}\)

Question

\(\int \dfrac{\cos \theta \,}{\sin ^{2}\theta +\sin \theta -6}\,d\theta \)

Question

\(\int \dfrac{\sin x}{\cos ^{2}x-2\cos x-8}dx\)

Question

\(\int \dfrac{\sin \theta \,}{\cos ^{3}\theta +\cos \theta }\,d\theta \)

Question

\(\int \dfrac{4\cos \theta \,}{\sin ^{3}\theta +2\sin \theta }\,d\theta \)

Question

\(\int \dfrac{e^{t}\,}{e^{2t}+e^{t}-2}\,dt\)

Question

\(\int \dfrac{e^{x}}{e^{2x}+e^{x}-6}\,dx\)

Question

\(\int \dfrac{e^{x}}{e^{2x}-1}dx \)

Question

\(\int \dfrac{dx}{e^{x}-e^{-x}}\)

Question

\(\int \dfrac{dt}{e^{2t}+1} \)

Question

\(\int \dfrac{dt}{e^{3t}+e^{t}} \)

Question

\(\int \dfrac{\sin x\cos x}{(\sin x - 1)^2}\,dx\)

Question

\(\int \dfrac{\cos x\sin x\,}{(\cos x-2)^2}\,dx\)

Question

\(\int\dfrac{\cos x}{ (\sin^2 x+9)^2 }\,dx\)

Question

\(\int \dfrac{\sin x}{ (\cos^2 x+4)^2 } \,dx\)

507

Question

Area Find the area under the graph of \(y=\dfrac{4}{x^{2}-4}\) from \(x=3\) to \(x=5\), as shown in the figure below.

Question

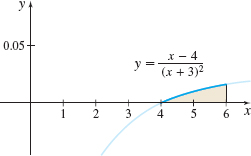
Area Find the area under the graph of \(y=\dfrac{x-4}{(x+3) ^{2}}\) from \(x=4\) to \(x=6\), as shown in the figure below.

Question

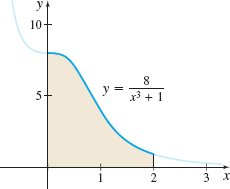
Area Find the area under the graph of \(y=\dfrac{8}{x^{3}+1}\) from \(x=0\) to \(x=2\), as shown in the figure below.

Question

Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=\dfrac{x}{x^{2}-4}\) and the \(x\)-axis from \(x=3\) to \(x=5\) about the \(x\) -axis, as shown in the figure below.

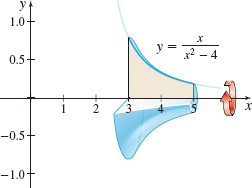
Question

1. Find the zeros of \(q( x) =x^{3}+3x^{2}-10x-24.\)
2. Factor \(q.\)
3. Find the integral \(\int \dfrac{3x-7}{x^{3}+3x^{2}-10x-24}dx.\)

Question

\(\int \dfrac{x\,dx}{3+\sqrt{x}} \)

Question

\(\int \dfrac{dx}{\sqrt{x}+2}\)

Question

\(\int \dfrac{dx}{x-\sqrt[3]{x}} \)

Question

\(\int \dfrac{x\,dx}{\sqrt[3]{x}-1}\)

Question

\(\int \dfrac{dx}{\sqrt{x}+\sqrt[3]{x}} \)

Question

\(\int \dfrac{dx}{3\sqrt{x}-\sqrt[3]{x}} \)

Question

\(\int \dfrac{dx}{\sqrt[3]{2+3x}}\)

Question

\(\int \dfrac{dx}{\sqrt[4]{1+2x}}\)

Question

\(\int \dfrac{x\,dx}{(1+x)^{3/4}}\)

Question

\(\int \dfrac{dx}{(1+x)^{2/3}} \)

Question

\(\int \dfrac{\sqrt[3]{x}+1}{\sqrt[3]{x}-1}dx \)

Question

\(\int \dfrac{dx}{\sqrt{x}(1+\sqrt[3]{x})^{2}}\)

Question

\(\int \dfrac{dx}{1-\sin x}\)

Question

\(\int \dfrac{dx}{1+\sin x} \)

Question

\(\int \dfrac{dx}{1-\cos x}\)

Question

\(\int \dfrac{dx}{3+2\cos x} \)

Question

\(\int \dfrac{2\,dx}{\sin x+\cos x}\)

Question

\(\int \dfrac{dx}{1-\sin x+\cos x}\)

Question

\(\int \dfrac{\sin x}{3+\cos x}dx\)

Question

\(\int \dfrac{dx}{\tan x-1}\)

Question

\(\int \dfrac{dx}{\tan x-\sin x}\)

Question

\(\int \dfrac{\sec x}{\tan x-2}dx \)

Question

\(\int \dfrac{\cot x\,}{1+\sin x}dx\)

Question

\(\int \dfrac{\sec x\,}{1+\sin x}dx\)

Question

\(\int_{0}^{\pi /2}\dfrac{dx}{\sin x+1}\)

Question

\(\int_{\pi /4}^{\pi /3}\dfrac{\csc x\,}{3+4\tan x}\,dx \)

Question

\(\int_{0}^{\pi /2}\dfrac{\cos x\,}{2-\cos x}\,dx\)

Question

\(\int_{0}^{\pi /4}\dfrac{4\,dx}{\tan x+1}\)

508

Question

Use a Weierstrass substitution to derive the formula \[ \int \csc x\,dx=\ln \sqrt{\dfrac{1-\cos x}{1+\cos x}}+C \]

Question

Show that the result obtained in Problem 88 is equivalent to \[ \int \csc x\,dx=\ln \,\vert \csc x-\cot x\vert +C \]

Question

Since \(\dfrac{d}{dx}\tanh ^{-1}x=\dfrac{1}{1-x^{2}}\), we might expect that \[ \int_{2}^{3}\dfrac{dx}{1-x^{2}} = \tanh ^{-1}3-\tanh ^{-1}2. \] Why is this incorrect? What is the correct result?

Question

Show that the two formulas below are equivalent. \[ \begin{eqnarray*} \int \sec x\,dx &=& \ln \,\vert \sec x+\tan x \vert +C\\ \int \sec x\,dx &=& \ln \left\vert \dfrac{1+\tan \dfrac{x}{2} }{1-\tan \dfrac{x}{2}}\right\vert +C \end{eqnarray*} \left[ {Hint:} \tan \dfrac{x}{2}=\dfrac{\sin \dfrac{x }{2}}{\cos \dfrac{x}{2}}=\dfrac{\sin ^{2}\left( \dfrac{x}{2}\right) }{\sin \left( \dfrac{x}{2}\right) \cos \left( \dfrac{x}{2}\right) }=\dfrac{1-\cos x }{\sin x}.\right] \]

Question

Use the methods of this section to find \(\int \dfrac{dx}{1+x^{4} }\). (Hint: Factor \(1+x^{4}\) into irreducible quadratics.)