7.6 Assess Your Understanding
518
Concepts and Vocabulary
Question
True or False The Trapezoidal Rule approximates an integral \(\int_{a}^{b}f(x)\,dx\) by replacing the graph of \(f\) with line segments.
Question
True or False Simpson’s Rule approximates an integral by using parabolic arcs.
Skill Building
For Problems 3 and 5, use the graph below to approximate the area \(A.\) Round answers to three decimal places.
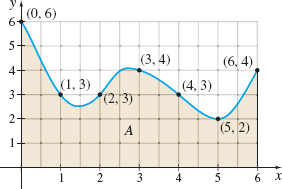
For Problems 4 and 6, use the graph below to approximate the area \(A.\) Round answers to three decimal places.
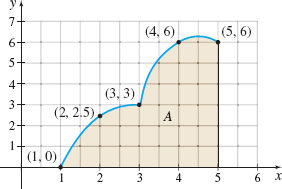
Question
Use the Trapezoidal Rule with \(n\) = 3 and \(n\) = 6 to approximate the area under the graph.
Question
Use the Trapezoidal Rule with \(n\) = 2 and \(n\) = 4 to approximate the area under the graph.
Question
Use Simpson’s Rule with \(n\) = 2 and \(n\) = 6 to approximate the area under the graph.
Question
Use Simpson’s Rule with \(n\) = 2 and \(n\) = 4 to approximate the area under the graph.
In Problems 7—12:
- Use the Trapezoidal Rule to approximate each integral.
 Estimate the error in using the approximation. Express the answer rounded to three decimal places.
Estimate the error in using the approximation. Express the answer rounded to three decimal places.- Find the number \(n\) of subintervals needed to guarantee that an approximation is correct to within 0.0001.
Question
\(\int_{\pi /2}^{\pi}\dfrac{\sin x}{x}dx\); \(n\) = 3
Question
\(\int_{3\pi /2}^{2\pi }\dfrac{\cos x}{x}dx\); \(n\) = 3
Question
\(\int_{0}^{1}e^{-x^{2}}\,dx\); \(n\) = 4
Question
\(\int_{0}^{1}e^{x^{2}}\,dx\); \(n\) = 4
Question
\(\int_{-1}^{0}\dfrac{dx}{\sqrt{1-x^{3}}};\) \(n\) = 4
Question
\(\int_{0}^{1}\dfrac{dx}{\sqrt{1+x^{3}}};\) \(n\) = 3
In Problems 13—18:
- Use Simpson’s Rule to approximate each integral.
 Estimate the error in using the approximation. Express the answer rounded to three decimal places.
Estimate the error in using the approximation. Express the answer rounded to three decimal places.- Find the number \(n\) of subintervals needed to guarantee that an approximation is correct to within 0.0001.
Question
\(\int_{1}^{2}\dfrac{e^x}{x}\,dx\); \(n\) = 4
Question
\(\int_{3\pi/2}^{2\pi} \dfrac{\cos x}{x} dx\); \(n\) = 4
Question
\(\int_{0}^{1}e^{-x^{2}}\,dx\); \(n\) = 4
Question
\(\int_{0}^{1}e^{x^{2}}\,dx\); \(n\) = 4
Question
\(\int^{0}_{-1}\dfrac{dx}{\sqrt{1-x^3}}\); \(n\) = 4
Question
\(\int_{0}^{1}\dfrac{dx}{\sqrt{1+x^2}}\); \(n\) = 4
Applications and Extensions
Question
- Show that \(\int_{1}^{2}\,\dfrac{dx}{x}=\ln 2.\)
- Use the Trapezoidal Rule with \(n = 5\) to approximate \(\int_{1}^{2}\,\dfrac{dx}{x}.\)
- Use Simpson’s Rule with \(n = 6\) to approximate \(\int_{1}^{2}\dfrac{\,dx}{x}\).
Question
Area Selected measurements of a function \(f\) are given in the table below. Use Simpson’s Rule to approximate the area enclosed by the graph of \(f\), the \(x\)-axis, and the lines \(x = 2\) and \(x = 4.4\).
| \(x\) | 2.0 | 2.4 | 2.8 | 3.2 | 3.6 | 4.0 | 4.4 |
| \(y\) | 3.03 | 4.61 | 5.80 | 6.59 | 7.76 | 8.46 | 9.19 |
Question
Arc Length Approximate the arc length of the graph of \(y = \sin x\) from \(x = 0\) to \(x = \dfrac{\pi}{2}\)
- using Simpson’s Rule with \(n = 4\).
- using the Trapezoidal Rule with \(n = 3\).
Question
Arc Length Approximate the arc length of the graph of \(y=e^{x}\) from \(x = 0\) to \(x = 4\)
- using Simpson’s Rule with \(n = 4\).
- using the Trapezoidal Rule with \(n = 8\).
Question
Work A gas expands from a volume of \(1\) cubic inch (in.\(^{3})\) to 2.5 in.\(^{3}\); values of the volume \(V\) and pressure \(p\) (in pounds per square inch) during the expansion are given in the table below. Find the total work \(W\) done in the expansion using Simpson’s Rule. (Hint: \(W=\int_{a}^{b}p\,dV)\).
| \(V\) | \(1\) | \(1.25\) | \(1.5\) | \(1.75\) | \(2\) | \(2.25\) | \(2.5\) |
| \(p\) | 68.7 | 55.0 | 45.8 | 39.3 | 34.4 | 30.5 | 27.5 |
Question
Work In the table below, \(F\) is the force in pounds acting on an object in its direction of motion and \(x\) is the displacement of the object in feet. Use the Trapezoidal Rule to approximate the work done by the force in moving the object from \(x = 0\) to \(x = 50\).
| \(x\) | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| \(F\) | 100 | 80 | 66 | 56 | 50 | 45 | 40 | 36 | 33 | 30 | 28 |
519
Question
Volume In the table below, \(S\) is the area in square meters of the cross section of a railroad track cutting through a mountain, and \(x\) meters is the corresponding distance along the line. Use the Trapezoidal Rule to find the number of cubic meters of earth removed to make the cutting from \(x = 0\) to \(x = 150\). See the figure below.
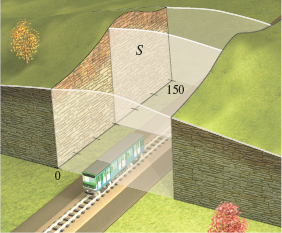
| \(x\) | 0 | 25 | 50 | 75 | 100 | 125 | 150 |
| \(S\) | 105 | 118 | 142 | 120 | 110 | 90 | 78 |
Question
Area Use Simpson’s Rule to approximate the surface area of the pond pictured in the figure.
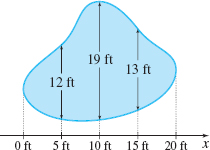
Question
Volume The area of the horizontal section of a reservoir is \(A\) square meters at a height \(x\) meters from the bottom. Corresponding values of \(A\) and \(x\) are given in the table below. Approximate the volume of water in the reservoir using the Trapezoidal Rule and also using Simpson’s Rule. See the figure.
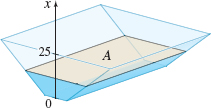
| \(x\) | 0 | 2.5 | 5 | 7.5 | 10 | 12.5 | 15 | 17.5 | 20 | 22.5 | 25 |
| \(A\) | 0 | 2510 | 3860 | 4870 | 5160 | 5590 | 5810 | 6210 | 6890 | 7680 | 8270 |
Question
Area A series of soundings taken across a river channel is given in the table below, where \(x\) meters is the distance from one shore and \(y\) meters is the corresponding depth of the water. Find its area by the Trapezoidal Rule.
| \(x\) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| \(y\) | 5 | 10 | 13.2 | 15 | 15.6 | 12 | 6 | 4 | 0 |
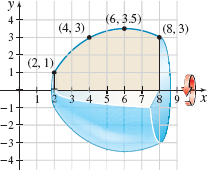
Question
Volume of a Solid of Revolution Use the Trapezoidal Rule with \(n = 3\) to approximate the volume of the solid of revolution formed by revolving the region shown in the figure below about the \(x\)-axis.
Question
Distance Traveled The speed \(v\), in meters per second, of an object at time \(t\) is given in the table below.
| \(t\) | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| \(v\) | 5.1 | 5.3 | 5.6 | 6.1 | 6.8 | 6.7 | 6.5 |
- Use the Trapezoidal Rule to approximate the distance \(s\) traveled by the object from \(t = 0\) to \(t = 3\).
- Use Simpson’s Rule to approximate the distance \(s\) traveled by the object from \(t = 0\) to \(t = 3\).
Question
Volume of a Solid of Revolution Approximate the volume of the solid of revolution in the figure below generated by revolving the region bounded by the graph of \(y=\sin x\) and the \(y\)-axis from \(x = 0\) to \(x=\dfrac{\pi}{2}\) about the \(y\)-axis
- using Simpson’s Rule with \(n = 4\).
- using the Trapezoidal Rule with \(n = 3\).

Question
Arc Length Use the Trapezoidal Rule to find the arc length of the ellipse \(9x^{2}+100y^{2}=900\) in the first quadrant from \(x = 0\) to \(x = 8\). Partition the interval into four equal subintervals, and round the answer to three decimal places.
Question
Approximate \(\int^{\pi}_0 f(x)\,dx\) if \(f(x)=\left\{ \begin{array}{c@{\quad}l@{\quad}l} \dfrac{\sin x}{x} & \hbox{if} & x\neq 0 \\ 1 & \hbox{if} & x=0 \end{array} \right. \)
- Use the Trapezoidal Rule with \(n = 6\).
- Use Simpson’s Rule with \(n = 6\).
Question
![]() Approximate \(\int_{-1}^{1}5e^{-x^{2}}dx\).
Approximate \(\int_{-1}^{1}5e^{-x^{2}}dx\).
- Use the Trapezoidal Rule with \(n = 20\) subintervals.
- Use Simpson’s Rule with \(n = 20\) subintervals.
- Use a CAS to find the integral.
520
Challenge Problems
Question
Let \(T_{n}\) be the approximation to \(\int_{a}^{b} f(x)\,dx\) given by the Trapezoidal Rule with \(n\) subintervals. Without using the error formula given in the text, show that \(\lim\limits_{n\,\rightarrow \,\infty}T_{n}=\int_{a}^{b}f(x)\,dx\).
Question
Show that if \(f(x)=Ax^{3}+Bx^{2}+Cx+D\), then Simpson’s Rule gives the exact value of \(\int_{a}^{b}f(x)\,dx\).
