7.1 Assess Your UnderstandingPrinted Page 478
Concepts and Vocabulary
True or False Integration by parts is based on the Product Rule for derivatives.
True
The integration by parts formula states that \(\int\! u\,dv\,{=}\) ______.
\(uv-\int v\,du\)
Skill Building
In Problems 3–30, use integration by parts to find each integral.
\(\int xe^{2x} dx\)
\(\dfrac{1}{2}xe^{2x} - \dfrac{1}{4}e^{2x} +C\)
\(\int xe^{-3x} dx\)
\(\int x\cos x~dx\)
\(x\sin x+\cos x + C\)
\(\int x\sin (3x)~dx\)
\(\int \sqrt{x}\ln x~dx\)
\(\dfrac{2}{3}x^{{3}/{2}}\ \ln \,x - \dfrac{4}{9}x^{{3}/{2}}+C\)
\(\int x^{-2}\ln x~dx\)
\(\int \cot^{-1}x~dx\)
\(x\cot^{-1} x + \dfrac{1}{2}\ln (x^2+1)+C\)
\(\int \sin^{-1}x~dx\)
\(\int (\ln x)^{2} dx\)
\(x(\ln x)^2 -2x \,\ln x + 2x +C\)
\(\int x(\ln x)^{2} dx\)
\(\int x^{2} \sin x~dx\)
\(-x^2 \,\cos x + 2x \,\sin x + 2 \,\cos x + C\)
\(\int x^{2}cosx~dx\)
\(\int x\cos^{2}x~dx\)
\(\dfrac{1}{2} x \cos x \sin x + \dfrac{1}{4} x^2 - \dfrac{1}{4} \sin^2 x + C\)
\(\int x\sin^{2}x~dx\)
\(\int x\sinh x~dx\)
\(x \,\cosh x - \sinh x + C\)
\(\int x\cosh x~dx\)
\(\int \cosh^{-1}x~dx\)
\(x \,\cosh^{-1} \,x - \sqrt{x^2-1}+C\)
\(\int \sinh^{-1}x~dx\)
\(\int \sin(\ln x)~dx\)
\(\dfrac{x}{2}[\sin (\ln x) - \cos (\ln x)]+C\)
\(\int \cos (\ln x)~dx\)
\(\int (\ln x)^{3} dx\)
\(x(\ln x)^3-3x(\ln x)^2+6x \,\ln x-6x+C\)
\(\int (\ln x)^{4} dx\)
\(\int x^{2}(\ln x)^{2} dx\)
\(\dfrac{1}{3} x^3 (\ln x)^2 - \dfrac{2}{9} x^3 \ln x + \dfrac{2}{27} x^3 + C\)
\(\int x^{3}(\ln x)^{2} dx\)
\(\int x^{2}\tan ^{-1}x~dx\)
\(\dfrac{1}{3} x^3 \tan^{-1} x - \dfrac{1}{6} x^2 +\dfrac{1}{6} \ln(1 + x^2) + C\)
\(\int x\tan ^{-1}x~dx\)
\(\int 7^{x} x~dx\)
\(\dfrac{7^x x}{\ln 7} - \dfrac{7^x}{(\ln 7)^2} + C\)
\(\int 2^{-x} x~dx\)
In Problems 31–38, use integration by parts to find each definite integral.
\(\int_{0}^{\pi}e^{x}\cos x~dx\)
\(-\dfrac{e^{\pi} + 1}{2}\)
\(\int_{0}^{1}x^{2} e^{-x}dx\)
\(\int_{0}^{2}x^{2} e^{-3x} dx\)
\(\dfrac{2}{27} - \dfrac{50}{27} e^{-6}\)
\(\int_{0}^{\pi/4}x\tan ^{2}x~dx\)
\(\int_{1}^{9}\ln \sqrt{x} dx\)
\(9 \,\ln 3 - 4\)
\(\int_{\pi/4}^{3\pi/4}x\csc ^{2} x~dx\)
\(\int^{e}_1 (\ln x)^{2} dx\)
\(e-2\)
\(\int_{0}^{\pi/4}x \sec^{2} x~dx\)
Applications and Extensions
Area Between Two Graphs In Problems 39 and 40, find the area of the region enclosed by the graphs of \(f\) and \(g\).
\(f(x)=3\ln x\) and \(g(x)=x\ln x, x \ge 1\)
\(\dfrac{9}{2} \ln 3 - 4\)
\(f(x)=4x\ln x\) and \(g(x)=x^{2}\ln x, x \ge 1\)
Area Under a Graph Find the area under the graph of \(y=e^{x}\sin x\) from \(0\) to \(\pi\).
\(\dfrac{e^{\pi} + 1}{2}\)
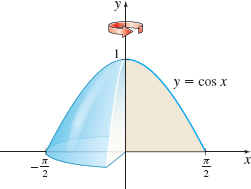
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=\cos x\) and the \(x\)-axis from \(x=0\) to \(x=\dfrac{\pi }{2}\) about the \(y\)-axis. See the figure below.
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=\sin x\) and the \(x\)-axis from \(x=0\) to \(x=\dfrac{\pi }{2}\) about the \(y\)-axis.
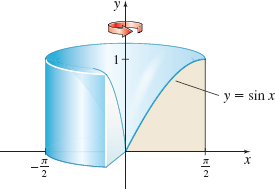
\(2\pi\)
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=x \sqrt{\sin x}\) and the \(x\)-axis from \(x=0\) to \(x=\dfrac{\pi }{2}\) about the \(x\)-axis.
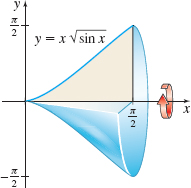
479
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=\ln x\) and the \(x\)-axis from \(x=1\) to \(x=e\) about the \(x\)-axis.
\(e\pi - 2\pi\)
 Area
Area- (a) Graph the functions \(f( x)=x^{3}e^{-3x}\) and \(g( x) =x^{2}e^{-3x}\) on the same set of coordinate axes.
- (b) Find the area enclosed by the graphs of \(f\) and \(g\).
 Damped Spring The displacement \(x\) of a damped spring at time \(t\), \(0 \le t \le 5\), is given by \(x=x( t)=3e^{-t}\cos (2t) +2e^{-t}\sin (2t)\).
Damped Spring The displacement \(x\) of a damped spring at time \(t\), \(0 \le t \le 5\), is given by \(x=x( t)=3e^{-t}\cos (2t) +2e^{-t}\sin (2t)\).- (a) Graph \(x=x( t)\).
- (b) Find the least positive number \(t\) that satisfies \(x(t) =0\).
- (c) Find the area under the graph of \(x=x(t)\) from \(t=0\) to the value of \(t\) found in (b).
- (a)
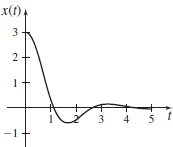
- (b) \(\dfrac{\pi}{2} + \dfrac{1}{2} \tan^{-1} \left(-\dfrac{3}{2}\right)\)
- (c) \(\approx 1.890\)
A function \(y=f( x)\) is continuous and differentiable on the interval \(( 2,6)\). If \(\int_{3}^{5}f( x)~dx=18\) and \(f( 3) =8\) and \(f( 5) =11,\) then find \(\int_{3}^{5}x f^{\prime}(x)~dx\).
In Problems 49–54, find each integral by first making a substitution and then integrating by parts.
\(\int \sin\sqrt{x}dx\)
\(2\sin \sqrt{x} - 2\sqrt{x}\cos \sqrt{x} +C\)
\(\int e^{\sqrt{x}}dx\)
\(\int \cos x \ln(\sin x)~dx\)
\((\sin x) \,\ln (\sin x)-\sin x + C\)
\(\int e^{x}\ln (2+e^{x}) dx\)
\(\int e^{4x}\cos e^{2x} dx\)
\(\dfrac{1}{2} e^{2x} \sin e^{2x} + \dfrac{1}{2} \cos e^{2x} + C\)
\(\int \cos x\tan ^{-1} (\sin x)~dx\)
Find \(\int x^{3}e^{x^{2}} dx\). (Hint: Let \(u=x^{2},dv=xe^{x^{2}} dx\).)
\(\dfrac{1}{2} x^2 e^{x^2} - \dfrac{1}{2} e^{x^2} + C \)
Find \(\int x^{n} \ln x~dx\); \(n \neq -1\), \(n\) real.
Find \(\int xe^{x}\cos x~dx\).
\(\dfrac{1}{2} e^x (x \sin x + x \cos x - \sin x) + C\)
Find \(\int xe^{x}\sin x~dx\).
In Problems 59–62, derive each reduction formula where \(n \gt 1\) is an integer.
\(\int x^{n}\sin ^{-1}x\,dx=\dfrac{x^{n+1}}{n+1}\sin^{-1}x-\dfrac{1}{n+1}\int \dfrac{x^{n+1}}{\sqrt{1-x^{2}}}\,dx\)
See the Student Solutions Manual.
\(\int \dfrac{dx}{(x^{2}+1)^{n+1}}=\left( 1-\dfrac{1}{2n}\right) \int \dfrac{dx}{(x^{2}+1)^{n}}+\dfrac{x}{2n(x^{2}+1)^{n}}\)
\(\int \sin^{n}x~dx=-\dfrac{\sin ^{n-1}x\cos x}{n}+\dfrac{n-1}{n}\int \sin ^{n-2}x\,dx\)
See the Student Solutions Manual.
\(\int \sin^{n}x \cos^{m} x~dx = -\dfrac{\sin^{n-1}x \cos^{m+1}x}{n+m} + \dfrac{n-1}{n+m}\int \sin^{n-2}x \cos^{m} xdx\)
where \(m \neq -n\), \(m \neq -1\)
- (a) Find \(\int x^{2}e^{5x}\,dx\).
- (b) Using integration by parts, derive a reduction formula for \(\int x^{n}e^{kx}\,dx\), where \(k \neq 0\) and \(n \ge 2\) is an integer, in which the resulting integrand involves \(x^{n-1}\).
- (a) \(\dfrac{1}{5} x^2 e^{5x} - \dfrac{2}{25} x e^{5x} + \dfrac{2}{125} e^{5x} + C\)
- (b) \(\int{x^{n} e^{kx}}\,dx = \dfrac{1}{k} x^n e^{kx} - \dfrac{n}{k} \int x^{n-1} e^{kx} dx\)
- (a) Assuming there is a function \(p\) for which \(\int x^{3}e^{x}dx\) \(=p( x) e^{x}\), show that \(p( x)+p^{\prime} (x) =x^{3}\).
- (b) Use integration by parts to find a polynomial \(p\) of degree 3 for which \(\int x^{3}e^{x}dx=p( x) e^{x}+C.\)
- (a) Use integration by parts with \(u=\sin x\) and \(dv=\cos x\,dx\) to find a function \(f\) for which \(\int \sin x\cos x~dx=f( x) +C_{1}\).
- (b) Use integration by parts with \(u=\cos x\) and \(dv=\sin x\,dx\) to find a function \(g\) for which \(\int \sin x\cos x~dx=g( x) +C_{2}\).
- (c) Use the trigonometric identity \(\sin (2x) =2\sin x\cos x\) and substitution to find a function \(h\) for which \[ \int \sin x\cos x~dx=h( x) +C_{3}.\]
- (d) Compare the functions \(f\) and \(g\). Find a relationship between \(C_{1}\) and \(C_{2}\).
- (e) Compare the functions \(f\) and \(h\). Find a relationship between \(C_{1}\) and \(C_{3}\).
- (a) \(f(x) = \dfrac{1}{2} \sin^2 x\)
- (b) \(g(x) = -\dfrac{1}{2} \cos^2 x\)
- (c) \(h(x) = -\dfrac{1}{4} \cos(2x)\)
- (d) \(C_2 = \dfrac{1}{2} + C_1\)
- (e) \(C_3 = \dfrac{1}{4} + C_1\)
Derive the formula \[ \int \ln (x+\sqrt{x^{2}+a^{2}})\,dx = x\ln (x+\sqrt{x^{2}+a^{2}}) -\sqrt{x^{2}+a^{2}}+C \]
Derive the formula \[ \int e^{ax}\sin (bx)~dx = \dfrac{e^{ax}[a\sin (bx)-b\cos (bx)]}{a^{2}+b^{2}} +C, a \gt 0, b\gt 0 \]
See the Student Solutions Manual.
Suppose \(F(x)=\int_{0}^{x}t\,g^{\prime }(t)\,dt\) for all \(x \ge 0\). Show that \(F(x)=\) \(xg(x)-\int_{0}^{x}g(t)\,dt\).
Use Wallis’ formulas, given below, to find each definite integral.
- \(\int_{0}^{\pi/2} \sin^{n}x~dx = \int_{0}^{\pi /2} \cos^{n}x~dx\) \(n \gt 1\) an integer \[=\left\{ \begin{array}{@{}l@{\qquad}l} \dfrac{(n-1)(n-3)\cdots (4)(2)}{n(n-2)\cdots (5)(3)(1)} & n \gt 1 \hbox{ is odd} \\ \dfrac{(n-1)(n-3)\cdots (5)(3)(1)}{n(n-2)\cdots (4)(2)}\left( \dfrac{\pi }{2} \right) & n\gt1\hbox{ is even} \end{array} \right.\]
- (a) \(\int_{0}^{\pi /2}\sin ^{6}x~dx\)
- (b) \(\int_{0}^{\pi /2}\sin ^{5}x~dx\)
- (c) \(\int_{0}^{\pi /2}\cos ^{8}x~dx\)
- (d) \(\int_{0}^{\pi /2}\cos ^{6}x~dx\)
- (a) \(\dfrac{5\pi}{32}\)
- (b) \(\dfrac{8}{15}\)
- (c) \(\dfrac{35\pi}{256}\)
- (d) \(\dfrac{5\pi}{32}\)
Challenge Problems
Derive Wallis’ formulas given in Problem 69. (Hint: Use the result of Problem 61.)
- (a) If \(n\) is a positive integer, use integration by parts to show that there is a polynomial \(p\) of degree \(n\) for which \[ \int x^{n}e^{x}dx=p( x) e^{x}+C \]
480
- (b) Show that \(p( x) +p^{\prime} ( x) =x^{n}\).
- (c) Show that \(p\) can be written in the form \[ p(x) = \sum \limits_{k=0}^{n}(-1)^{k} \dfrac{n!}{(n-k)!}x^{n-k} \]
- (a) If \(n\) is a positive integer, use integration by parts to show that there is a polynomial \(p\) of degree \(n\) for which \[ \int x^{n}e^{x}dx=p( x) e^{x}+C \]
See the Student Solutions Manual.
Show that for any positive integer \(n\), \[ \begin{eqnarray*} \hspace{-20pc}\int_{0}^{1}e^{x^{2}} dx \\ = e\cdot \!\left[ 1-\frac{2}{3}+\frac{4}{15}-\frac{8}{105}+\cdots +\frac{(-1)^{n}2^{n}}{(2n+1)(2n-1)\cdots 3\cdot 1}\right] \\+ (-1)^{n+1} \cdot \frac{2^{n+1}}{(2n+1)(2n-1)\cdots 3\cdot 1} \int_{0}^{1}x^{2n+2}e^{x^{2}}dx \end{eqnarray*} \]
Use integration by parts to show that if \(f\) is a polynomial of degree \(n \ge 1\), then \(\int f( x) e^{x}dx=g( x) e^{x}+C\) for some polynomial \(g( x)\) of degree \(n\).
See the Student Solutions Manual.
Start with the identity \(f(b)-f(a)=\int_{a}^{b}f^{\prime}(t)\,dt\) and derive the following generalizations of the Mean Value Theorem for Integrals:
- (a) \(f(b)-f(a)=f^{\prime} (a)(b-a)- \int_{a}^{b}f^{\prime \prime}(t)(t-b)\,dt\)
- (b) \( f(b)-f(a)=f^{\prime} (a)(b-a)+\dfrac{f^{\prime\prime} (a)}{2}(b-a)^{2} + \int_{a}^{b}\dfrac{f^{\prime \prime \prime} (t)}{2}(t-b)^{2} dt \)
If \(y=f(x)\) has the inverse function given by \(x=f^{-1}(y)\), show that \[ \begin{equation*} \int_{a}^{b}f(x)\,dx+\int_{f(a)}^{f(b)}f^{-1}(y)\,dy=bf(b)-af(a) \end{equation*} \]
See the Student Solutions Manual.
- (a) When integration by parts is used to find \(\int e^{x}\cosh x~dx\), what happens? Explain.
- (b) Find \(\int e^{x}\cosh x~dx\) without using integration by parts.
