Question

True or False To find \(\int \cos ^{5}x\,dx,\) factor out \(\cos x\) and use the identity \(\cos ^{2}x=1-\sin ^{2}x.\)

Question

True or False To find \(\int \sin (2x) \cos (3x) \,dx,\) use a product-to-sum identity.

Question

\(\int \cos ^{5}x\,dx\)

Question

\(\int \sin ^{3}x\,dx\)

Question

\(\int \sin ^{6}x\,dx\)

Question

\(\int \cos ^{4}x\,dx\)

Question

\(\int \sin ^{2}\left( \pi x\right) \,dx\)

Question

\(\int \cos ^{4}(2x) \,dx\)

Question

\(\int_{0}^{\pi }\cos ^{5}x~dx\)

Question

\(\int_{-\pi /3}^{\pi /3}\sin ^{3}x\,dx\)

Question

\(\int \sin ^{3}x\cos ^{2}x\,dx\)

Question

\(\int \sin ^{4}x\cos ^{3}x\,dx\)

Question

\(\int \sin ^{2}x\cos ^{2}x\,dx\)

Question

\(\int \sin ^{4}x\cos ^{2}x\,dx\)

Question

\(\int \sin x\cos ^{1/3}x\,dx\)

Question

\(\int \cos ^{3}x\sin ^{1/2}x\,dx\)

Question

\(\int \sin ^{2}\left(\dfrac{x}{2}\right) \cos ^{3}\left( \dfrac{x}{2}\right) \,dx\)

Question

\(\int \sin ^{3}(4x) \cos ^{3}(4x) \,dx \)

Question

\(\int \tan ^{3}x\sec ^{2}x\,dx\)

Question

\(\int \tan x\sec ^{5}x\,dx\)

Question

\(\int \tan ^{2}x\sec ^{2}x\,dx\)

Question

\(\int \tan ^{5}x\sec ^{2}x\,dx\)

Question

\(\int \tan ^{2}x\sec ^{3}x\,dx\)

Question

\(\int \tan ^{4}x\,\sec x\,dx\)

Question

\(\int \cot ^{3}x\csc x\,dx\)

Question

\(\int \cot ^{3}x\csc ^{2}x\,dx\)

Question

\(\int \sin (3x) \cos x\,dx\)

Question

\(\int \sin x\cos (3x) \,dx\)

Question

\(\int \cos x\cos (3x) \,dx\)

Question

\(\int \cos (2x) \cos x\,dx \)

Question

\(\int \sin (2x) \sin (4x) \,dx\)

Question

\(\int \sin (3x) \sin x\, dx\)

Question

\(\int_{0}^{\pi /2}\sin (2x) \sin x\,dx\)

Question

\(\int_{0}^{\pi }\cos x\cos (4x) \,dx\)

Question

\(\int \sin ^{2}x\cos x\,dx\)

Question

\(\int \sin ^{3}x\cos x\,dx\)

Question

\(\int \dfrac{\sin x\,dx}{\cos ^{2}x}\)

Question

\(\int \dfrac{\cos x\,dx}{\sin ^{4}x}\)

Question

\(\int \cos ^{3}(3x) \,dx\)

Question

\(\int \sin ^{5}(3x) \,dx\)

Question

\(\int_{0}^{\pi }\sin ^{3}x\cos ^{5}x\,dx\)

Question

\(\int_{0}^{\pi /2}\sin ^{3}x\cos ^{3}x\,dx\)

Question

\(\int \tan ^{3}x\,dx\)

Question

\(\int \cot ^{5}x\,dx\)

Question

\(\int \dfrac{\sec ^{6}x}{\tan ^{3}x}\,dx\)

Question

\(\int \tan ^{1/2}x\sec ^{2}x\,dx\)

Question

\(\int \csc ^{2}x\cot ^{5}x\,dx\)

Question

\(\int \cot x\csc ^{2}x\,dx\)

487

Question

\(\int \cot(2x) \csc^{4}(2x)~dx\)

Question

\(\int \cot^{2}(2x) \csc^{3}(2x)dx\)

Question

\(\int_{0}^{\pi /4}\tan^{4}x\sec^{3}xdx \)

Question

\(\int_{0}^{\pi /4}\tan^{2}x\sec xdx\)

Question

\(\int \sin \left( \dfrac{x}{2}\right) \cos \left( \dfrac{3x}{2}\right)dx\)

Question

\(\int \cos (-x) \sin (4x)dx\)

Question

\(\int \sin \left( \dfrac{x}{2}\right) \sin \left( \dfrac{3x}{2}\right)dx\)

Question

\(\int \cos (\pi x) \cos ( 3\pi x)dx\)

Question

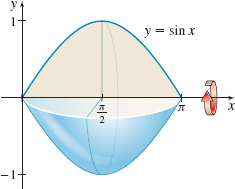
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=\sin x\) and the \(x\)-axis from \(x=0\) to \(x=\pi \) about the \(x\)-axis. See the figure below.

Question

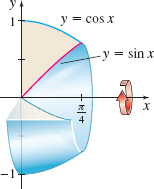
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graphs of \(y=\cos x\), \(y=\sin x\), and \(x=0\) from \(x=0\) to \(x=\dfrac{\pi }{4}\) about the \(x\)-axis.

Question

Average Value

1. Find the average value of \(f( x) =\sin x\cos ^{4}x\) over the interval \([ 0,\,\pi ] \).
2. Give a geometric interpretation to the average value.
3. Use graphing technology to graph \(f\) and the average value on the same screen.

Question

Rectilinear Motion The acceleration \(a\) of an object at time \(t\) is given by \(a(t) =\cos ^{2}t\sin t\) m\(/\)s\(^{2}\). At \(t=0\), the object is at the origin and its speed is 5m\(/\)s. Find its distance from the origin at any time \(t\).

Question

Area and Volume Let \(A\) be the area of the region in the first quadrant bounded by the graphs of \(y=\sec x\), \(y=2\sin x\), and the \(y\)-axis.

1. Find \(A\).
2. Find the volume of the solid of revolution generated by revolving the region about the \(x\)-axis.

Question

1. Use technology to graph the function \(f( x) =\sin^{n}x,\) \(0 \le x \le \pi\), for \(n=5\), \(n=10\), \(n=20\), and \(n=50\).
2. Find \(\int_{0}^{\pi }\sin ^{n}xdx\) correct to three decimal places for \(n=5\), \(n=10\), \(n=20\), and \(n=50\).
3. What does (a) suggest about the shape of the graph of \(f( x) =\sin ^{n}x\), \(0 \le x \le \pi\), as \(n\rightarrow \infty\).
4. Find \(\lim\limits_{n\rightarrow \infty }\int_{0}^{\pi }\sin ^{n}x~dx\).

Question

Find \(\int \sin ^{4}x\,dx\).

1. Using the methods of this section.
2. Using the reduction formula given in Problem 61 in Section 7.1.
3. Verify that both results are equivalent.
4. Use a CAS to find \(\int \sin ^{4}x~dx\).

Question

1. Use the substitution \(u=\sin x\) to find a function \(f\) for which \[ \int \sin x\cos x\,dx=f(x)+C_{1}. \]
2. Use the substitution \(u=\cos x\) to find a function \(g\) for which \[ \int \sin x\cos x\,dx=g(x)+C_{2}. \]
3. Use the trigonometric identity \(\sin (2x)=2\sin x\cos x\) to find a function \(h\) for which \[ \int \sin x\cos x\,dx=h(x)+C_{3}. \]
4. Compare the functions \(f\) and \(g\). Find a relationship between \(C_{1}\) and \(C_{2}\).
5. Compare the functions \(f\) and \(h\). Find a relationship between \(C_{1}\) and \(C_{3}\).

Question

Derive a formula for \(\int \sin (mx) \sin (nx) \,dx,\quad m ≠ n\).

Question

Derive a formula for \(\int \sin (mx) \cos (nx) \,dx,\quad m ≠ n\).

Question

Derive a formula for \(\int \cos (mx) \cos (nx) \,dx,\quad m ≠ n\).

Question

Use the substitution \(\sqrt{x}\,=\,\sin y\) to find \(\int_{0}^{1/2}\dfrac{\sqrt{x}}{\sqrt{1-x}}\,dx\). \(\bigg(\)Hint: sin\(^{2}y\,{=}\,\dfrac{1\,{-}\,\cos (2y)}{2}.\bigg)\)

Question

Use an appropriate substitution to show that \[ \int_{0}^{\pi /2}\sin ^{n}\theta \,d\theta =\,\int_{0}^{\pi /2}\cos ^{n}\theta \,d\theta . \]

Question

1. What is wrong with the following?
   
   
2. Find \(\int_{0}^{\pi }\cos ^{4}x~dx\).