7.3 Integration Using Trigonometric Substitution: Integrands Containing √(a2-x2), √(x2+a2), or √(x2-a2), a > 0
488
OBJECTIVES
When you finish this section, you should be able to:
- Find integrals containing \(\sqrt{ a^{2}- x^{ 2}}\) (p. 488)
- Find integrals containing \(\sqrt{ x^{ 2} + a^{ 2}}\) (p. 489)
- Find integrals containing \(\sqrt{ x^{ 2}- a^{ 2}}\) (p. 491)
- Use trigonometric substitution to find definite integrals (p. 492)
When an integrand contains a square root of the form \(\sqrt{a^{2}-x^{2}}\), \(\sqrt{x^{2}+a^{2}}\), or \(\sqrt{x^{2}-a^{2}}\), \(a \gt 0\), an appropriate trigonometric substitution will eliminate the radical and sometimes transform the integral into a trigonometric integral like those studied earlier.
The substitutions to use for each of the three types of radicals are given in Table 2.
| Integrand Contains | Substitution | Based on the Identity |
|---|---|---|
| \(\sqrt{a^{2}-x^{2}}\) | \(x=a\sin \theta\), \(-\dfrac{\pi }{2} \le \theta \, \le \dfrac{\pi }{2}\) | \(1-\sin ^{2}\theta =\cos ^{2}\theta\) |
| \(\sqrt{x^{2}+a^{2}}\) | \(x=a\tan \theta\), \(-\dfrac{\pi }{2} \lt\theta \lt\dfrac{\pi }{2}\) | \(\tan ^{2}\theta +1=\sec ^{2}\theta\) |
| \(\sqrt{x^{2}-a^{2}}\) | \(x=a\sec \theta\), \(0 \le \theta \lt\dfrac{\pi }{2}\), \(\pi \le \theta \lt\dfrac{3\pi }{2}\) | \(\sec ^{2}\theta -1=\tan ^{2}\theta\) |
CAUTION
Be careful to use the restrictions on each substitution. They guarantee the substitution is a one-to-one function, which is a requirement for using substitution.
Although the substitutions to use can be memorized, it is often easier to draw a right triangle and derive them as needed. Each substitution is based on the Pythagorean Theorem. By placing the sides \(a\) and \(x\) on a right triangle appropriately, the third side of the triangle will represent one of the three types of radicals, as shown in Figure 3.
NEED TO REVIEW?
Right triangle trigonometry is discussed in Appendix A.4, pp. A-27 to A-31.
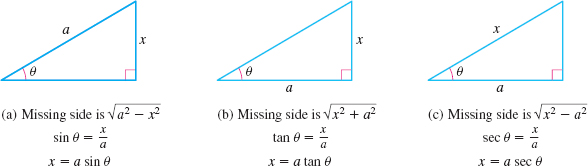
1 Find Integrals Containing √(a2-x2)
When an integrand contains a radical of the form \(\sqrt{a^{2}-x^{2}}\), \(a\gt0\), we use the substitution \(x=a\sin \theta\), \(-\dfrac{\pi }{2} \le \theta \le \dfrac{\pi }{2}\). Substituting \(x=a\sin \theta\), \(-\dfrac{\pi }{ 2} \le \theta \le \dfrac{\pi }{2}\), in the expression \(\sqrt{a^{2}-x^{2}}\) eliminates the radical as follows: \[ \begin{array}{rcl@{\quad}l} \sqrt{a^{2}-x^{2}} &=&\sqrt{a^{2}-a^{2}\sin ^{2}\theta } & {\color{#0066A7}{\hbox{Let \(x=a \sin \theta\); \(-\dfrac{\pi }{2} \le \theta \le \dfrac{\pi }{2}\). }}}\\ &=&a\sqrt{1-\sin ^{2}\theta } & {\color{#0066A7}{\hbox{Factor out \(a^{2}\); \(a>0\).}}}\\ &=&a\sqrt{\cos ^{2}\theta } & {\color{#0066A7}{\hbox{\(1- \sin ^{2} \theta =\cos ^{2} \theta\)}}} \\ &=&a\cos \theta &{\color{#0066A7}{\hbox{\(\cos \theta \ge 0\) since \(- \dfrac{\pi }{2} \le \theta \le \dfrac{\pi }{2}\)}}} \end{array} \]
489
Finding an Integral Containing \(\sqrt{4-x^{2}}\)
Find \(\int \dfrac{dx}{x^{2}\sqrt{4-x^{2}}}\).
NOTE
We exclude \(\theta =-\dfrac{\pi}{2}\) and \(\theta =\dfrac{\pi}{2}\) because they lead to \(x=\pm 2\), resulting in \(\sqrt{{4-x}^{2}}=0\).
Solution The integrand contains the square root \(\sqrt{4-x^{2}}\) that is of the form \(\sqrt{a^{2}-x^{2}}\), where \(a=2\). We use the substitution \(x=2\sin \theta\), \(-\dfrac{\pi }{2} \lt\theta \lt\dfrac{\pi }{2}\). Then \(dx=2\cos \theta \,d\theta\). Since \[ \begin{eqnarray*} {\sqrt{4-x^{2}}} \underset{\underset{\color{#0066A7}{\hbox{\(x=2\sin \theta\)}}}{\color{#0066A7}{\uparrow }}} {=} {\sqrt{4-4\sin ^{2}\theta }}=2{\sqrt{1-\sin ^{2}\theta }}=2{\sqrt{\cos ^{2}\theta }} \underset{\underset{\color{#0066A7}{\hbox{\(\text {cos}~\theta \gt 0~\text {since} -\dfrac{\pi}{2} \lt \theta \lt \dfrac{\pi}{2}\)}}}{\color{#0066A7}{\uparrow}}}{=}2\cos \theta \end{eqnarray*} \]
we have \[ \int\! \frac{dx}{x^{2}\sqrt{4-x^{2}}}=\int\! \frac{2\cos \theta \,d\theta }{ (4\sin ^{2}\theta )(2\cos \theta )}=\int\! \dfrac{d\theta }{4\sin ^{2}\theta }= \frac{1}{4}\int \csc ^{2}\theta \,d\theta =-\frac{1}{4}\cot \theta +C \]
The original integral is a function of \(x\), but the solution above is a function of \(\theta\). To express \(\cot \theta\) in terms of \(x\), refer to the right triangles drawn in Figure 4.
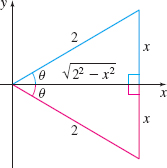
Using the Pythagorean Theorem, the third side of each triangle is \(\sqrt{ 2^{2}-x^{2}}=\sqrt{4-x^{2}}\). So, \[ \cot \theta =\dfrac{\sqrt{4-x^{2}}}{x} \qquad -\dfrac{\pi }{2} \lt\theta \lt \dfrac{\pi }{2} \]
Then \[ \int \dfrac{dx}{x^{2}\sqrt{4-x^{2}}}=-\frac{1}{4}\cot \theta +C=-\frac{1}{4}\frac{\sqrt{4-x^{2}}}{x}+C=-\frac{\sqrt{4-x^{2}}}{4x}+C \]
Alternatively, trigonometric identities can be used to express \(\cot \theta \) in terms of \(x\). Using identities, we get \[ \begin{eqnarray*} \cot \theta &=&\dfrac{\cos \theta }{\sin \theta }\underset{\underset{\underset{\color{#0066A7}{\hbox{\(\cos \theta >0\)}}}{\color{#0066A7}{\hbox{\(\cos^{2}\theta =1-\sin ^{2}\theta\)}}}}{\color{#0066A7}{\uparrow }}}{=} \dfrac{\sqrt{1-\sin ^{2}\theta }}{\sin \theta } \underset{\underset{\underset {\color{#0066A7}{\hbox{\(\sin \theta \,=\dfrac{x}{2}\)}}} {\color{#0066A7}{\hbox{\(x\,=\,2\sin \theta\)}}}} {\color{#0066A7}{\uparrow }}}{=} \dfrac{\sqrt{1-\left( \dfrac{x}{2}\right)^{2}}}{\dfrac{x}{2}}=\dfrac{2\sqrt{ 1-\dfrac{x^{2}}{4}}}{x}=\dfrac{\sqrt{4-x^{2}}}{x} \end{eqnarray*} \]
NOW WORK
Problem 7.
2 Find Integrals Containing √(x2+a2)
When an integrand contains a radical of the form \(\sqrt{x^{2}+a^{2}}\), \(a>0\), we use the substitution \(x=a\tan \theta\), \(-\dfrac{\pi }{2} \lt\theta \lt \dfrac{\pi }{2}\). Substituting \(x=a\tan \theta\), \(-\dfrac{\pi }{2} \lt\theta \lt \dfrac{\pi }{2}\), in the expression \(\sqrt{x^{2}+a^{2}}\) eliminates the radical as follows: \[ \begin{eqnarray*} \sqrt{x^{2}+a^{2}}\underset{\underset{\color{#0066A7}{\hbox{\(x=a\tan \theta\)}}} {\color{#0066A7}{\uparrow}}}{=} \sqrt{a^{2}\tan^{2}\theta +a^{2}} \underset{\underset{\underset{\color{#0066A7}{\hbox{\(a \gt 0\)}}}{\color{#0066A7}{\hbox{Factor out \(a\),}}}}{\color{#0066A7}{\uparrow }}}{=} a\sqrt{\tan^{2}\theta +1}=a\sqrt{\sec^{2}\theta} \underset{\underset{\underset{\color{#0066A7}{\hbox{\(\text {since} -\dfrac{\pi }{2} \lt \theta \lt \dfrac{\pi }{2}\)}}}{\color{#0066A7}{\hbox{\(\text {sec}~\theta \gt 0\)}}}} {\color{#0066A7}{\uparrow }}}{=}a\sec\theta \end{eqnarray*} \]
490
Finding an Integral Containing \(\sqrt{x^{2}+9}\)
Find \(\int \frac{dx}{(x^{2}+9)^{3/2}}\).
Solution The integral contains a square root \((x^{2}+9)^{3/2}= \big( \sqrt{x^{2}+9}\big) ^{3}\) that is of the form \(\sqrt{x^{2}+a^{2}},\) where \(a=3\). We use the substitution \(x=3\tan \theta\), \(-\dfrac{\pi }{2} \lt \theta \lt \dfrac{\pi }{2}\). Then \(dx=3\sec ^{2}\theta d\theta\). Since \[ \begin{eqnarray*} (x^{2}+9)^{3/2}\underset{\underset{\color{#0066A7}{\hbox{\(x=3\tan \theta\)}}}{\color{#0066A7}{\uparrow}}}{=}(9\tan^{2}\theta +9)^{3/2}=9^{3/2}(\tan^{2}\theta +1)^{3/2}\underset{\underset{\color{#0066A7}{\hbox{\(\tan^{2}\theta +1=\sec ^{2}\theta\)}}}{\color{#0066A7}{\uparrow}}}{=}27(\sec^{2}\theta)^{3/2}\underset{\underset{\color{#0066A7}{\hbox{\(\sec \theta >0\)}}}{\color{#0066A7}{\uparrow}}}{=}27\sec ^{3}\theta \end{eqnarray*} \]
we have \[ \begin{equation*} \int \frac{dx}{(x^{2}+9)^{3/2}}=\int \frac{3\sec ^{2}\theta d\theta }{27\sec ^{3}\theta }=\frac{1}{9}\int \frac{d\theta }{ \sec \theta }=\frac{1}{9}\int \cos \theta d\theta =\frac{1}{9}\sin \theta +C \end{equation*} \]
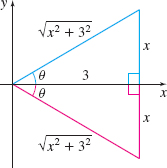
To express the solution in terms of \(x,\) use either the right triangles in Figure 5 or identities.
From the right triangles, the hypotenuse is \(\sqrt{x^{2}+3^{2}}=\sqrt{x^{2}+9 }\). So, \(\sin \theta =\dfrac{x}{\sqrt{x^{2}+9}}.\) Then \[ \int \frac{dx}{(x^{2}+9)^{3/2}}=\dfrac{1}{9}\sin \theta +C=\dfrac{x}{9 \sqrt{x^{2}+9}}+C \]
NOW WORK
Problem 15.
NOTE
An integral containing \(\sqrt{x^{2}+a^{2}}\), \(a \gt 0\), can also be found using the substitution \(x=a \sinh \theta\), since \[ \begin{eqnarray*} \sqrt{x^{2}+a^2} &=& \sqrt{a^2\sinh ^2 \theta +a^2} \\[2pt] &=& a \sqrt{\sinh ^{2} \theta +1} \\[2pt] &=&a \sqrt{\cosh ^{2} \theta} = a \cosh \theta \end{eqnarray*} \]
Try it!
Finding the Integral \(\int (4x^{2}+9) ^{1/2}dx\)
Find \(\int ( 4x^{2}+9) ^{1/2}dx\).
Solution \(\int (4x^{2}+9)^{1/2}dx =\int \sqrt{(2x)^{2}+3^{2}} dx\)
We use the substitution \(2x=3\tan \theta\), \(-\dfrac{\pi }{2} \lt \theta \lt \dfrac{\pi}{2}.\) Then \(dx=\dfrac{3}{2}\sec ^{2}\theta d\theta\) and \[ \begin{eqnarray*} \int ( 4x^{2}+9) ^{1/2}dx &=&\dfrac{3}{2}\int \sqrt{9\tan ^{2}\theta +9}\sec ^{2}\theta\, d\theta =\dfrac{9}{2}\int \sqrt{\tan ^{2}\theta +1}\sec ^{2}\theta\, d\theta \\[5pt] &=&\dfrac{9}{2}\int \sec ^{3}\theta \,d\theta \\[5pt] &=&\dfrac{9}{2}\left[ \dfrac{1}{2}\sec \theta \tan \theta +\dfrac{1}{2}\ln \left\vert \sec \theta +\tan \theta \right\vert \right] +C \end{eqnarray*} \]

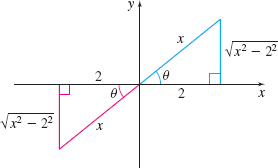
To express the solution in terms of \(x\), refer to the right triangles drawn in Figure 6.
Using the Pythagorean Theorem, the hypotenuse of each triangle is \(\sqrt{ (2x) ^{2}+9}=\sqrt{4x^{2}+9}.\) So, \[ \sec \theta =\frac{\sqrt{4x^{2}+9}}{3}\quad \hbox{and}\quad \tan \theta =\frac{2x}{3} \quad -\frac{\pi }{2} \lt \theta \lt \frac{\pi }{2} \]
491
Then \[ \begin{eqnarray*} \int ( 4x^{2}+9) ^{1/2}dx &=&\frac{9}{4}\left[ \sec \theta \tan \theta +\ln \left\vert \sec \theta +\tan \theta \right\vert \right] +C \nonumber \\[2pt] &=&\frac{9}{4}\left[ \frac{\sqrt{4x^{2}+9}}{3}\cdot \frac{2x}{3}+\ln \left\vert \frac{\sqrt{4x^{2}+9}}{3}+\frac{2x}{3}\right\vert \right] +C \nonumber \\[3pt] &=&\frac{9}{4}\left[ \frac{2x\sqrt{4x^{2}+9}}{9}+\ln \frac{2x+\sqrt{4x^{2}+9}}{3}\right] +C \end{eqnarray*} \]
In general, if the integral contains \(\sqrt{b^{2}x^{2}+a^{2}},\) we use the substitution \(bx=a\tan \theta\) \(\left( x=\dfrac{a}{b}\tan \theta \right)\), \(-\dfrac{\pi }{2} \lt \theta \lt \dfrac{\pi }{2}.\)
NOW WORK
Problem 45.
3 Find Integrals Containing √(x2-a2)
NOTE
The substitution \(x=a\cosh \theta \) can also be used for integrands containing \(\sqrt{x^{2}-a^{2}}\).
When an integrand contains \(\sqrt{x^{2}-a^{2}}\), \(a\gt0\), we use the substitution \(x=a\sec \theta\), \(0 \le \theta \lt \frac{\pi }{2}\), \(\pi \le \theta \lt \dfrac{3\pi }{2}.\) Then

Finding an Integral Containing \(\sqrt{x^{2}-4}\)
Find \(\int \frac{\sqrt{x^{2}-4}}{x} dx\).
Solution The integrand contains the square root \(\sqrt{x^{2}-4}\) that is of the form \(\sqrt{x^{2}-a^{2}},\) where \(a=2\). We use the substitution \(x=2\sec \theta\), \(0 \le \theta \lt \dfrac{\pi }{2},\) \(\pi \le \theta \lt\dfrac{3\pi }{2}\). Then \(dx=2\sec \theta \tan \theta~d\theta.\) Since \[ \begin{eqnarray*} \sqrt{x^{2}-4} \underset{\underset{\color{#0066A7}{\hbox{\(x=2 \sec \theta\)}}}{\color{#0066A7}{\uparrow}}}{=}\sqrt{4\sec ^{2}\theta -4}=2\sqrt{\sec ^{2}\theta -1}=2\sqrt{\tan^{2}\theta } \underset{\underset{\underset{\color{#0066A7}{\hbox{since \(0 \le \theta \lt \dfrac{\pi }{2}, \pi \le \theta \lt \dfrac{3\pi}{2}\)}}}{\color{#0066A7}{\hbox{\(\tan \theta \ge 0\)}}}}{\color{#0066A7}{\uparrow}}}{=} 2\tan \theta \end{eqnarray*} \]
we have \[ \begin{eqnarray*} \int \frac{\sqrt{x^{2}-4}}{x}dx&=&\int \frac{(2\tan \theta )(2\sec \theta \tan \theta \,d\theta )}{2\sec \theta }=2\int \tan ^{2}\theta d\theta \underset{\underset{\color{#0066A7}{\hbox{\(\tan^{2}\theta = \sec^{2}\theta -1\)}}}{\color{#0066A7}{\uparrow}}}{=}2\int (\sec^{2}\theta -1) d\theta \\ &=&2\int \sec^{2}\theta d\theta -2\int d\theta =2\tan \theta -2\theta +C \end{eqnarray*} \]
To express the solution in terms of \(x\), we use either the right triangles in Figure 7 or trigonometric identities.
Using identities, we find, \[ \begin{eqnarray*} \tan \theta \underset{\underset{\underset{{\color{#0066A7}{\hbox{\(\tan \theta \ge 0\)}}}}{\color{#0066A7}{\hbox{\(\tan^{2}\theta =\sec^{2}\theta -1\)}}}}{\color{#0066A7}{\uparrow}}}{=}\sqrt{\sec^{2}\theta -1}= \sqrt{\frac{x^{2}}{4}-1}=\frac{1}{2}\sqrt{x^{2}-4} \end{eqnarray*} \]
Also since \(\sec \theta =\dfrac{x}{2},\) \(0 \le \theta \lt \dfrac{\pi }{2},\) \(\pi \le \theta \lt \dfrac{3\pi }{2},\) the inverse function \(\theta =\sec ^{-1}\dfrac{x }{2}\) is defined.
492
Then \[ \int\frac{\sqrt{x^{2}-4}}{x}dx=2\tan \theta -2\theta+C=\sqrt{x^{2}-4} -2\sec ^{-1} \frac{x}{2}+C \]
NOW WORK
Problem 29.
4 Use Trigonometric Substitution to Find Definite Integrals
Trigonometric substitution is also useful when finding certain types of definite integrals.

Finding the Area Enclosed by an Ellipse
Find the area \(A\) enclosed by the ellipse \(\dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}=1.\)
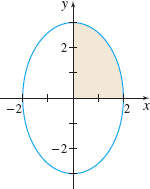
Solution Figure 8 illustrates the ellipse. Since the ellipse is symmetric with respect to both the \(x\)-axis and the \(y\)-axis, the total area \(A\) of the ellipse is four times the shaded area in the first quadrant, where \(0 \le x \le 2\) and \(0 \le y \le 3.\)
We begin by expressing \(y\) as a function of \(x.\) \[ \begin{eqnarray*} \frac{x^{2}}{4}+\frac{y^{2}}{9} &=&1 \\[4.5pt] \frac{y^{2}}{9} &=&1-\frac{x^{2}}{4}=\frac{4-x^{2}}{4} \\[4.5pt] y^{2} &=&\dfrac{9}{4}( 4-x^{2}) \\[4.5pt] y &=&\dfrac{3}{2}\sqrt{4-x^{2}}\qquad {\color{#0066A7}{\hbox{\(y \ge 0\)}}} \end{eqnarray*} \]
So, the area \(A\) of the ellipse is four times the area under the graph of \(y=\dfrac{3}{2}\sqrt{4-x^{2}},\) \(0 \le x \le 2.\) That is, \[ A=4 \int_{0}^{2}\dfrac{3}{2}\sqrt{4-x^{2}}\,dx =6\int_{0}^{2}\sqrt{4-x^{2}}\,dx \]
Since the integrand contains a square root of the form \(\sqrt{a^{2}-x^{2}}\) with \(a=2,\) we use the substitution \(x=2\sin \theta\), \(-\frac{\pi}{2} \le \theta \le \frac{\pi }{2}\). Then \(dx=2\cos \theta \,d\theta\). The new limits of integration are:
- When \(x=0\), \(2\sin \theta =0\), so \(\theta =0\).
- When \(x=2\), \(2\sin \theta =2\), so \(\sin \theta =1\) and \(\theta =\dfrac{\pi }{2}\).
Then \[ \begin{eqnarray*} A&=&6\int_{0}^{2}\sqrt{4-x^{2}}\,dx=6\int_{0}^{\pi /2}\sqrt{4-4\sin^{2}\theta }\cdot 2\cos \theta \,d\theta\\ &=&6\int_{0}^{\pi /2}2\sqrt{1-\sin^{2}\theta }\cdot 2\cos \theta \,d\theta = 24\int_{0}^{\pi /2}\sqrt{\cos ^{2}\theta }\cdot \cos \theta \,d\theta\nonumber \\ &\underset{\underset{\color{#0066A7}{\hbox{\(\cos \theta \ge 0\)}}}{\color{#0066A7}{\uparrow }}}{=}&24\int_{0}^{\pi /2}\cos^{2}\theta \,d\theta \underset{\underset{\color{#0066A7}{\hbox{\(\cos^{2}\theta =\frac{1+\cos (2\theta )}{2}\)}}}{\color{#0066A7}{\uparrow }}}{=} \frac{24}{2}\int_{0}^{\pi /2}\left[1+\cos (2\theta ) \right] \,d\theta \nonumber \\ & =&12\left[ \theta +\frac{1}{2}\sin (2\theta ) \right]_{0}^{\pi /2}=12\left( \frac{\pi }{2}+0\right) =6\pi \end{eqnarray*} \]
The area of the ellipse is \(6\pi\) square units.
NOW WORK
Problem 63.
493
In Example 5, we changed the limits of integration to find the definite integral, so there was no need to change back to the variable \(x.\) But it is not always easy to obtain new limits of integration, as we see in the next example.
NEED TO REVIEW?
The two approaches to finding a definite integral using the method of substitution are discussed in Section 5.6, pp. 387-393.
Use Trigonometric Substitution to Find a Definite Integral
Find the area under the graph of \(y=\sqrt{x^{2}-1}\) (the upper half of the right branch of the hyperbola \(y^{2}=x^{2}-1\)) from 1 to 3. See Figure 9.

Solution The area \(A\) we seek is \(A= \int_{1}^{3}\sqrt{x^{2}-1 }\,dx\). The integral contains a square root of the form \(\sqrt{x^{2}-a^{2}}\), where \(a=1\), so we use the trigonometric substitution \(x=\sec \theta \), \( 0 \le \theta \lt\dfrac{\pi }{2},\) \(\pi \le \theta \lt\dfrac{3\pi }{2}.\) Then \(dx=\sec \theta \tan \theta \,d\theta \). Since the upper limit \(x=3\) does not result in a nice angle \((\theta =\sec ^{-1}\,3)\), we find the indefinite integral first and then use the Fundamental Theorem of Calculus.
With \(x=\sec \theta \hbox{ and } dx=\sec \theta \tan \theta d\theta ,\) we have \[ \begin{eqnarray*} A&=&\int \sqrt{x^{2}-1}\,dx=\int \sqrt{\sec ^{2}\theta -1}\sec \theta \tan \theta \,d\theta =\int \tan \theta \cdot \sec \theta \tan \theta \,d\theta\\[5pt] &=&\int \tan ^{2}\theta \sec \theta d\theta \end{eqnarray*} \]
Since \(\tan \theta \) is raised to an even power and \(\sec \theta \) to an odd power, we use the identity \(\tan ^{2}\theta =\sec ^{2}\theta -1.\)Then \[ \begin{eqnarray*} A &=&\int \sqrt{x^{2}-1}\,dx=\int \tan ^{2}\theta \sec \theta d\theta =\int \left( \sec ^{2}\theta -1\right) \sec \theta d\theta\\[4pt] &=&\int \sec ^{3}\theta d\theta -\int \sec \theta d\theta \\[4pt] &=&\dfrac{1}{2}\left[ \sec \theta \tan \theta +\ln \left\vert \sec \theta +\tan \theta \right\vert \right] -\ln \left\vert \sec \theta +\tan \theta \right\vert +C\\[4pt] &=&\dfrac{1}{2}\sec \theta \tan \theta -\dfrac{1}{2}\ln \left\vert \sec \theta +\tan \theta \right\vert +C \end{eqnarray*} \]
RECALL
\(\int \sec ^{3}\theta d\theta =\\ \dfrac{1}{2}\left[ \sec \theta \tan \theta +\ln \left\vert \sec \theta +\tan \theta \right\vert \right]\). Either integrate by parts, or use the reduction formula.
Now we express \(\tan \theta \) in terms of \(x=\sec \theta ,\) and apply the Second Fundamental Theorem of Calculus. \[ \begin{eqnarray*} A&=&\int_{1}^{3}\sqrt{x^{2}-1}\, dx\underset{\underset{\underset{\color{#0066A7}{\hbox{\(\tan \theta =\sqrt{x^{2} -1}\)}}}{\color{#0066A7}{\hbox{\(\sec \theta =x\)}}}}{\color{#0066A7}{\uparrow }}} {=}\left[ \frac{1}{2}x\sqrt{x^{2}-1}-\frac{1}{2}\ln \left\vert x+ \sqrt{x^{2}-1}\right\vert \right] _{1}^{3}\\ &=&\dfrac{3}{2}\sqrt{8}-\dfrac{1}{2}\ln ( 3+\sqrt{8}) =3\sqrt{2} -\dfrac{1}{2}\ln (3+2\sqrt{2}) \end{eqnarray*} \]
NOW WORK
Problem 53.