Question

True or False To find \(\int \sqrt{a^{2}-x^{2}}\,dx\), the substitution \(x=a\sin \theta\), \(-\dfrac{\pi }{2} \le \theta \le \dfrac{ \pi }{2}\), can be used.

Question

Multiple Choice To find \(\int \sqrt{x^{2}+16}\,dx\), use the substitution \(x=\)[(a) \(4\sin \theta ,\) (b) \(\tan \theta ,\) (c) \( 4\sec \theta ,\) (d) \(4\tan \theta \)].

Question

Multiple Choice To find \(\int \sqrt{x^{2}-9} \,dx\), use the substitution \(x=\)[(a) \(\sec \theta ,\) (b) \(3\sin \theta ,\) (c) \(3\sec \theta ,\) (d) \(3\tan \theta \)].

Question

Multiple Choice To find \(\int \sqrt{25-4x^{2}}\,dx\), use the substitution \(x= \bigg[\)(a) \(\dfrac{5}{2}\tan \theta ,\) (b) \(\dfrac{5}{2} \sin \theta ,\) (c) \(\dfrac{2}{5}\sin \theta ,\) (d) \(\dfrac{2}{5}\sec \theta \bigg]\).

Question

\(\int \sqrt{4-x^{2}} dx\)

Question

\(\int \sqrt{16-x^{2}} dx\)

Question

\(\int \dfrac{x^{2}}{\sqrt{16-x^{2}}} dx\)

Question

\(\int \dfrac{x^{2}}{\sqrt{36-x^{2}}} dx\)

Question

\(\int \dfrac{\sqrt{4-x^{2}}}{x^{2}} dx\)

Question

\(\int \dfrac{\sqrt{9-x^{2}}}{x^{2}} dx\)

Question

\(\int x^{2}\sqrt{4-x^{2}} dx\)

Question

\(\int x^{2}\sqrt{1-16x^{2}} dx\)

Question

\(\int \dfrac{dx}{(4-x^{2})^{3/2}}\)

Question

\(\int \dfrac{dx}{(1-x^{2})^{3/2}}\)

Question

\(\int \sqrt{4+x^{2}} dx\)

Question

\(\int \sqrt{1+x^{2}} dx\)

Question

\(\int \dfrac{dx}{\sqrt{x^{2}+16}}\)

Question

\(\int \dfrac{dx}{\sqrt{x^{2}+25}}\)

Question

\(\int {\sqrt{1+9x^{2}}} dx\)

Question

\(\int {\sqrt{9+4x^{2}}} dx\)

Question

\(\int \dfrac{x^{2}}{\sqrt{4+9x^{2}}} dx\)

Question

\(\int \dfrac{x^{2}}{\sqrt{x^{2}+16}} dx\)

Question

\(\int \dfrac{dx}{x^{2}\sqrt{x^{2}+4}}\)

Question

\(\int \dfrac{dx}{x^{2}\sqrt{4x^{2}+1}}\)

Question

\(\int \dfrac{dx}{(x^{2}+4)^{3/2}}\)

Question

\(\int \dfrac{dx}{(x^{2}+1)^{3/2}}\)

Question

\(\int \dfrac{x^{2}}{\sqrt{x^{2}-25}} dx\)

Question

\(\int \dfrac{x^{2}}{\sqrt{x^{2}-16}} dx\)

Question

\(\int \dfrac{\sqrt{x^{2}-1}}{x} dx\)

Question

\(\int \dfrac{\sqrt{x^{2}-1}}{x^{2}} dx\)

Question

\(\int \dfrac{dx}{x^{2}\sqrt{x^{2}-36}}\)

Question

\(\int \dfrac{dx}{x^{2}\sqrt{x^{2}-9}}\)

Question

\(\int \dfrac{dx}{\sqrt{4x^{2}-9}}\)

Question

\(\int \dfrac{dx}{\sqrt{9x^{2}-4}}\)

Question

\(\int \dfrac{dx}{(x^{2}-9)^{3/2}}\)

Question

\(\int \dfrac{dx}{(25x^{2}-1)^{3/2}}\)

Question

\(\int \dfrac{x^{2}\,dx}{(x^{2}-9)^{3/2}}\)

Question

\(\int \dfrac{x^{2}\,dx}{(x^{2}-4)^{3/2}}\)

Question

\(\int \dfrac{x^{2}\,dx}{16+x^{2}}\)

Question

\(\int \dfrac{x^{2}\,dx}{1+16x^{2}}\)

Question

\(\int \sqrt{4-25x^{2}} dx\)

Question

\(\int \sqrt{9-16x^{2}} dx\)

Question

\(\int \dfrac{dx}{(4-25x^{2})^{3/2}}\)

Question

\(\int \dfrac{dx}{(1-9x^{2})^{3/2}}\)

Question

\(\int \sqrt{4+25x^{2}} dx\)

Question

\(\int \sqrt{9+16x^{2}} dx\)

Question

\(\int \dfrac{dx}{x^{3}\sqrt{x^{2}-16}}\)

Question

\(\int \dfrac{dx}{x^{3}\sqrt{x^{2}-1}}\)

Question

\(\int_{0}^{1}\sqrt{1-x^{2}} dx\)

Question

\(\int_{0}^{1/2}\sqrt{1-4x^{2}} dx\)

Question

\(\int_{0}^{1}\sqrt{1+x^{2}} dx\)

Question

\(\int_{0}^{2}\dfrac{x^{2}}{\sqrt{9+x^{2}}} dx\)

Question

\(\int_{4}^{5}\dfrac{x^{2}}{\sqrt{x^{2}-9}} dx\)

Question

\(\int_{1}^{2}\dfrac{x^{2}}{\sqrt{4x^{2}-1}} dx\)

Question

\(\int_{0}^{2}\dfrac{x^{2}\,dx}{(16-x^{2})^{3/2}}\)

Question

\(\int_{0}^{1}\dfrac{x^{2}\,dx}{(25-x^{2})^{3/2}}\)

Question

\(\int_{0}^{3}\dfrac{x^{2}\,dx}{9+x^{2}}\)

Question

\(\int_{0}^{1}\dfrac{x^{2}}{25+x^{2}} dx\)

Question

Area of an Ellipse Find \(\int \sqrt{a^{2}-x^{2}} dx\) and use it to find the area enclosed by the ellipse \(\dfrac{x^{2}}{a^{2}}+\dfrac{ y^{2}}{b^{2}}=1\).

Question

Area of a Semicircle

1. Find \({\int_{0}^{2}{\sqrt{4-x^{2}} \,dx}}\) by interpreting the integral as a certain area and using elementary geometry.
2. Find \({\int_{0}^{2}{\sqrt{4-x^{2}}\,dx}}\) using a trigonometric substitution.
3. Find the area of the semicircle \(y=\sqrt{a^{2}-x^{2}},\)\(-a \le x \le a \), using integration.

Question

Average Value Find the average value of the function \(f( x) =\dfrac{1}{\sqrt{9-4x^{2}}}\) over the interval [0,1].

Question

Average Value Find the average value of the function \(f( x) =\sqrt{x^{2}-4}\) the interval [2,7].

Question

Area Under a Graph Find the area under the graph of \(y=\dfrac{x^{3}}{\sqrt{9-x^{2}}}\) from \(x=0\) to \(x=2\).

Question

Area Under a Graph Find the area under the graph of \(y=x\sqrt{ 16-x^{2}},\)\(x \ge 0\).

495

Question

Area Under a Graph Find the area under the graph of \(y=\dfrac{ x^{2}}{\sqrt{x^{2}-1}}\)from \(x=3\) to \(x=5\).

Question

Hydrostatic Force A round window of radius \(2\) meters ( m) is built into the side of a large, fresh-water aquarium tank. If the center of the window is \(3 \hbox{m}\) below the water line, find the force due to hydrostatic pressure on the window. (Hint: The mass density of fresh water is \({\small \rho =1000}\hbox{kg}/\hbox{m}^{3}.)\)

Question

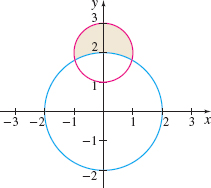
Area of a Lune A lune is a crescent-shaped area formed when two circles intersect.

1. Find the area of the smaller lune formed by the intersection of the two circles \(x^{2}+y^{2}=4\) and \(x^{2}+\left( y-2\right) ^{2}=1\), as shown in the figure.
2. What is the area of the larger lune?

Question

Area Find the area enclosed by the hyperbola \(\dfrac{x^{2}}{9}-\dfrac{y^{2}}{16}=1\) and the line \(x=6\).

Question

Arc Length Find the length of the graph of the parabola \( y=5x-x^{2}\)that lies above the \(x\)-axis.

Question

Arc Length Find the length of the graph of \(y=\ln x\) from \(x= \dfrac{\sqrt{3}}{3}\) to \(x=\sqrt{3}\).

Question

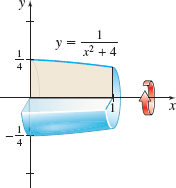
Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=\dfrac{1}{x^{2}+4}\) and the \(x\)-axis from \(x=0\) to \(x=1\) about the \(x\) -axis. See the figure.

Question

Volume of a Solid of Revolution Find the volume of the solid of revolution generated by revolving the region bounded by the graphs of \(y= \dfrac{1}{\sqrt{9-x^{2}}}\), \(y=0\), \(x=0\), and \(x=2\) about the \(x\)-axis.

Question

\(\int \dfrac{dx}{\sqrt{1-(x-2)^{2}}}\)

Question

\(\int \sqrt{4-(x+2)^{2}}dx\)

Question

\(\int \dfrac{dx}{\sqrt{(x-1)^{2}-4}}\)

Question

\(\int \dfrac{dx}{(x-2)\sqrt{(x-2)^{2}+9}}\)

Question

\(\int e^{x}\sqrt{25-e^{2x}}dx\)

Question

\(\int e^{x}\sqrt{4+e^{2x}}dx\)

Question

\(\int x\sin ^{-1}x\,dx\)

Question

\(\int x\cos ^{-1}x\,dx\)

Question

Find \(\int \sqrt{x^{2}+a^{2}}\,dx\)

1. By using a trigonometric substitution
2. By using substitution with a hyperbolic function

Question

\(\int \dfrac{dx}{\sqrt{a^{2}-x^{2}}}=\sin ^{-1} \dfrac{x}{a} +C\)

Question

\(\int \dfrac{dx}{a^{2}+x^{2}}=\dfrac{1}{a}\tan ^{-1} \dfrac{x}{a} +C\)

Question

\(\int \dfrac{dx}{x\sqrt{x^{2}-a^{2}}}=\dfrac{1}{a}\sec ^{-1} \dfrac{x}{a} +C\)

Question

\(\int \dfrac{dx}{\sqrt{x^{2}-a^{2}}}=\ln \left| \dfrac{x+\sqrt{x^2-a^2}}{a} \right| +C \)

Question

\(\int \dfrac{dx}{\sqrt{x^{2}+a^{2}}}=\ln \big| x+\sqrt{x^{2}+a^{2}}\big| +C\)

Question

Find \(\int \dfrac{dx}{\sqrt{3x-x^2}}\)

Question

Derive the formula \(\int \sqrt{x^{2}-a^{2}}dx=\dfrac{1}{2}x \sqrt{x^{2}-a^{2}}-\dfrac{1}{2}a^{2}\ln \vert x+\sqrt{x^{2}-a^{2}}\vert + C, a \gt 0.\)

Question

Find \(\int \dfrac{\,dx}{\sqrt{x^{2}+a^{2}}}\), \(a\gt0\), using the substitution \(u=\sinh ^{-1} \dfrac{x}{a} \). Express your answer in logarithmic form.

Question

Find \(\int \dfrac{\sec ^{2}x}{\sqrt{\tan ^{2}x-6\tan x+8}}\,dx\).