9.6 Area in Polar Coordinates
OBJECTIVES
When you finish this section, you should be able to:
- Find the area of a region enclosed by the graph of a polar equation (p. 678)
- Find the area of a region enclosed by the graphs of two polar equations (p. 681)
- Find the surface area of a solid of revolution obtained from the graph of a polar equation (p. 682)
RECALL
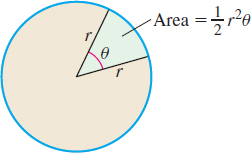
The area \(A\) of the sector of a circle of radius \(r\) formed by a central angle of \(\theta \) radians is \(A=\dfrac{1}{2} r^{2} \theta \).
In this section, we find the area of a region enclosed by the graph of a polar equation and two rays that have the pole as a common vertex. The technique used is similar to that used in Chapter 5, except, instead of approximating the area using rectangles, we approximate the area using sectors of a circle. Figure 48 illustrates the area of a sector of a circle.
1 Find the Area of a Region Enclosed by the Graph of a Polar Equation
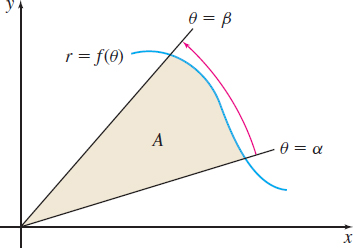
In Figure 49, \(r=f(\theta )\) is a function that is nonnegative and continuous on the interval \(\alpha \leq \theta \leq \beta \). Let \(A\) denote the area of the region enclosed by the graph of \(r=f(\theta )\) and the rays \(\theta =\alpha \) and \(\theta =\beta \), where \(0\leq \alpha \lt\beta \leq 2\pi \). It is helpful to think of the region \(R\) as being “swept out” by rays, beginning with the ray \(\theta =\alpha \) and continuing to the ray \(\theta =\beta \).
We partition the closed interval \([\alpha ,\beta ]\) into \(n\) subintervals: \[ \begin{equation*} \lbrack \alpha ,\theta _{1}], [\theta _{1},\theta _{2}], \ldots , [\theta _{i-1},\theta _{i}], \ldots , [\theta _{n-1},\beta ] \end{equation*} \]

each of length \(\Delta \theta =\dfrac{\beta -\alpha }{n}.\) As shown in Figure 50, we select an angle \(\theta _{i}\)* in each subinterval \([\theta _{i-1},\theta _{i}]\). The quantity \(\dfrac{1}{2}[ f(\theta _{i}\hbox{*})] ^{2}\Delta \theta \) is the area of the circular sector with radius \(r=f(\theta _{i}\) *\()\) and central angle \(\Delta \theta \). The sums of the areas of these sectors \[ \begin{equation*} \sum_{i=1}^{n}\frac{1}{2}[ f(\theta _{i}\hbox{*})] ^{2}\Delta\theta \end{equation*} \]
are an approximation of the area \(A\) we seek. As the number \(n\) of subintervals increases, the sums \(\sum\limits_{i=1}^{n}\dfrac{1}{2}\,\left[ f(\theta _{i}\hbox{*})\right] ^{2}\Delta \theta \) become better approximations to the total area \(A\). The sums \(\sum\limits_{i=1}^{n} \dfrac{1}{2} [ f(\theta _{i}\hbox{*}) ] ^{2}\Delta \theta \) are Riemann sums, and since \(r=f( \theta) \) is continuous, the limit exists and equals a definite integral. \[ \lim\limits_{n \rightarrow \infty }\sum\limits_{i=1}^{n} \dfrac{1}{2} [ f(\theta _{i}\hbox{*})] ^{2}\Delta \theta =\int_{\alpha }^{\beta }\dfrac{1}{2} [ f(\theta )] ^{2}d \theta =\int_{\alpha }^{\beta }\dfrac{1}{2}r^{2}d\theta \]
679
THEOREM Area in Polar Coordinates
If \(r=f(\theta )\) is nonnegative and continuous on the closed interval \([ \alpha ,\beta ] ,\) where \(\alpha \lt\beta \) and \(\beta -\alpha \leq 2\pi \), then the area \(A\) of the region enclosed by the graph of \(r=f(\theta )\) and the rays \(\theta =\alpha \) and \(\theta =\beta \) is given by \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{{A=\int_{\alpha }^{\beta }\dfrac{1}{2}r^{2}~d\theta}}}\]
NEED TO REVIEW?
The definite integral is discussed in Section 5.2, pp. 353-359.
Be sure to graph the equation \(r=f(\theta ),\;\alpha \leq \theta \leq \beta \), before using the formula. In drawing the graph, include the rays \( \theta =\alpha \), indicating the start, and \(\theta =\beta \), indicating the end, of the region whose area is to be found. These rays determine the limits of integration in the area formula.

Finding the Area Enclosed by a Part of a Cardioid
Find the area of the region enclosed by the cardioid \(r=1-\sin \theta ,\; 0\leq \theta \leq \dfrac{\pi }{2}.\)
Solution The cardioid represented by \(r=1-\sin \theta \) is shown in Figure 51(a) and the area enclosed by the cardioid from \(\theta = 0\) to \(\theta = \dfrac{\pi}{2}\) is shaded.
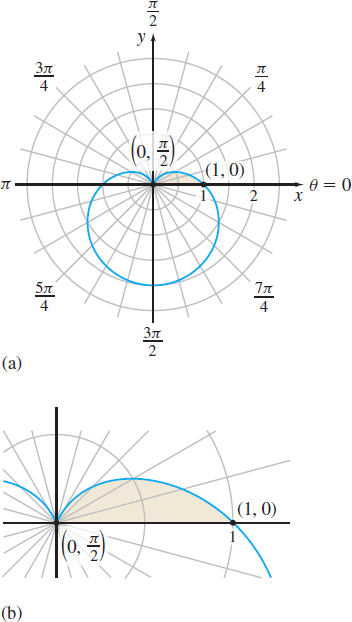
The region is swept out beginning with the ray \( \theta =0\) and ending with the ray \(\theta =\dfrac{\pi }{2}\), as shown in Figure 51(b). The limits of integration are \(0\) and \(\dfrac{\pi }{2}\) and the area \(A\) is \[ \begin{eqnarray*} A&=&\int_{\alpha }^{\beta }\frac{1}{2}r^{2}\,d\theta =\int_{0}^{\pi /2}\frac{1 }{2}(1-\sin \theta )^{2}\,d\theta =\frac{1}{2}\int_{0}^{\pi /2}(1-2\sin \theta +\sin ^{2}\theta )~d\theta \\[6pt] &=&\dfrac{1}{2}\int_{0}^{\pi /2}\left\{ 1-2\sin \theta +\frac{1}{2}[ 1-\cos ( 2\theta ) ] \right\} d\theta \qquad {\color{#0066A7}{\sin ^{2}\theta =\dfrac{1-\cos ( 2\theta )}{2}}} \\\\[5pt] &=&\frac{1}{2}\int_{0}^{\pi /2}\left[ \frac{3}{2}-2\sin \theta -\frac{1}{2}\cos ( 2\theta ) \right] d\theta\\[5pt] &=&\dfrac{1}{2}\left[ \dfrac{3}{2}\,\theta +2\cos \theta -\dfrac{1}{4}\sin ( 2\theta ) \right] _{0}^{\pi /2}=\dfrac{ 3\pi -8}{8} \end{eqnarray*} \]
NOW WORK
Problem 9.
Finding the Area Enclosed by a Cardioid
Find the area enclosed by the cardioid \(r=1-\sin \theta \).
Solution Look again at the cardioid in Figure 51(a). The region enclosed by the cardioid is swept out beginning with the ray \(\theta =0\) and ending with the ray \(\theta =2\pi \). So, the limits of integration are \(0\) and \(2\pi ,\) and the area \(A\) is \[ A=\int_{0}^{2\pi }\frac{1}{2}(1-\sin \theta )^{2}~d\theta =\frac{1}{2} \left[ \frac{3}{2}\theta +2 \cos \theta -\frac{1}{4}~\sin ( 2\theta ) \right] _{0}^{2\pi }=\frac{3\pi }{2} \]
NOW WORK
Problem 13.
680
Finding the Area Enclosed by a Rose
Find the area enclosed by the graph of \(r=2\cos ( 3\theta ) \), a rose with three petals.

Solution Figure 52 shows the rose. The area of the blue shaded region in quadrant I equals one-sixth of the area \(A\) enclosed by the graph.* The shaded region in quadrant I is swept out beginning with the ray \(\theta =0.\) It ends at the point \(( 0,\theta ) ,\) \(0\lt\theta \lt\dfrac{\pi }{2},\) where \(\theta \) is the solution of the equation. \[ \begin{eqnarray*} 2\cos ( 3\theta ) &=&0\qquad 0\lt\theta \lt\dfrac{\pi }{2} \\[4pt] \cos ( 3\theta ) &=&0 \\[4pt] 3\theta &=&\dfrac{\pi }{2}+2k\pi \\[4pt] \theta &=&\dfrac{\pi }{6}+\dfrac{2k\pi }{3} \end{eqnarray*} \]
* We need to exploit symmetry here since there are intervals on which \(r\lt0,\) and the area formula requires that \(r>0.\)
Since \(0\lt\theta \lt\dfrac{\pi }{2},\) we have \(\theta =\dfrac{\pi }{6}.\) The area of the shaded region in quadrant I swept out by the rays \(\theta =0\) and \(\theta =\dfrac{\pi }{6}\) is given by \(\int_{0}^{\pi /6}\dfrac{1}{2} r^{2}d\theta ,\) and the area \(A\) of the region we seek is \(6\) times this area. \[ \begin{eqnarray*} A &=& 6\int_{0}^{\pi /6}\dfrac{1}{2}r^{2}\,d\theta =3\int_{0}^{\pi /6} 4\cos ^{2}( 3\theta ) ~d\theta =12\int_{0}^{\pi /6}\cos ^{2}( 3\,\theta )~d\theta\\[4pt] &=& 12\int_{0}^{\pi /6}\frac{1+\cos ( 6\theta ) }{2}~d\theta\qquad {\color{#0066A7}{\hbox{\(\cos ^{2}( 3\theta ) =\dfrac{1+\cos ( 6\theta ) }{2}\)}}}\\\\[4pt] &=&6 \left[ \theta +\dfrac{1}{6}\sin ( 6\theta ) \right] _{0}^{\pi /6}=6\left( \frac{\pi }{6}\right) =\pi \end{eqnarray*} \]
NEED TO REVIEW?
Solving trigonometric equations is discussed in Section P.7, pp. 61-63.
NOW WORK
Problem 17.
Finding the Area Enclosed by a Limaçon
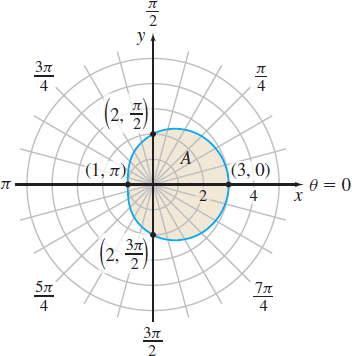
Find the area of the region enclosed by the limaçon \(r=2+\cos \theta \).
Solution Figure 53 shows the graph of \(r=2+\cos \theta\), a limaçon without an inner loop.
We see that the region above the polar axis equals the region below it, so the area \(A\) of the region enclosed by the limaçon equals twice the area of the region enclosed by \(r=2+\cos \theta \) and swept out by the rays \(\theta =0\) and \(\theta =\pi \). \[ \begin{eqnarray*} A& =&2\int_{0}^{\pi }\dfrac{1}{2}r^{2}d\theta =\int_{0}^{\pi }(2+\cos \theta )^{2}\,d\theta =\int_{0}^{\pi }(4+4\cos \theta +\cos ^{2}\theta )\,d\theta \notag \\[4pt] &=& \int_{0}^{\pi }\left[ 4+4\cos \theta +\dfrac{1+\cos ( 2\theta ) }{2}\right] d\theta \qquad{\color{#0066A7}{\cos ^{2}\theta =\dfrac{1+\cos ( 2\theta ) }{2}}} \\[4pt]\\[4pt] & =&\left[ 4\theta +4\sin \theta +\frac{\theta }{2}+\frac{1}{4}\sin ( 2\theta ) \right] _{0}^{\pi }=\frac{9\pi }{2} \end{eqnarray*} \]
NOW WORK
Problem 21.
2 Find the Area of a Region Enclosed by the Graphs of Two Polar Equations
681
To find the area \(A\) of the region enclosed by the graphs of two polar equations, we begin by graphing the equations and finding their points of intersection, if any.
Finding the Area of the Region Enclosed by the Graphs of Two Polar Equations
Find the area of the region that lies outside the cardioid \(r=1+\cos \theta \) and inside the circle \(r=3\cos \theta \).
Solution We begin by graphing each equation. See Figure 54(a). Then we find the points of intersection of the two graphs by solving the equation, \[ \begin{eqnarray*} 3\cos \theta & =&1+\cos \theta \\[3pt] 2\cos \theta & =&1 \\[3pt] \cos \theta & =&\frac{1}{2} \end{eqnarray*} \] \[ \begin{equation*} \theta =-\frac{\pi }{3}\;\hbox{or}\;\theta =\frac{\pi }{3} \end{equation*} \]
The graphs intersect at the points \(\left( \dfrac{3}{2},-\dfrac{\pi }{3} \right) \) and \(\left( \dfrac{3}{2},\dfrac{\pi }{3}\right) \).

The area \(A\) of the region that lies outside the cardioid and inside the circle is shown as the shaded portion in Figure 54(b). Notice that the area \( A\) is the difference between the area of the region enclosed by the circle \( r=3\cos \theta \) swept out by the rays \(\theta =-\dfrac{\pi }{3}\) and \( \theta =\dfrac{\pi }{3}\), and the area of the region enclosed by the cardioid \(r=1+\cos \theta \) swept out by the same rays. So, \[ \begin{array}{@rcl} A& =&\int_{-\pi /3}^{\pi /3}\frac{1}{2}(3\cos \theta )^{2}d\theta -\int_{-\pi /3}^{\pi /3}\frac{1}{2}(1+\cos \theta )^{2}d\theta =\frac{1}{2} \int_{-\pi /3}^{\pi /3}[ 9\cos ^{2}\theta -( 1+2\cos \theta +\cos^{2}\theta ) ] \,d\theta \notag \\[12pt] & =&\frac{1}{2}\int_{-\pi /3}^{\pi /3}(8\cos ^{2}\theta -1-2\cos \theta )~d\theta = \frac{1}{2}\int_{-\pi /3}^{\pi /3} \left[ 8\left( \frac{1+\cos ( 2\theta ) }{2}\right) -1-2\cos \theta \right] d\theta \notag \\[12pt] & =&\frac{1}{2}\int_{-\pi /3}^{\pi /3}[ 3+4\cos ( 2\theta ) -2\cos \theta ] ~d\theta =\frac{1}{2}\Big[ 3\theta +2\sin ( 2\theta ) -2\sin \theta \Big] _{-\pi /3}^{\pi /3}=\pi \end{array} \]
NOW WORK
Problem 23.
682
CAUTION The circle and the cardioid shown in Figure 54(a) actually intersect in a third point, the pole. The pole is not identified when we solve the equation to find the points of intersection because the pole has coordinates \(( 0,\pi ) \) on \(r=1+\cos \theta \), but it has coordinates \(\left( 0,\dfrac{\pi }{2}\right) \) and \(\left( 0,\dfrac{3\pi }{2} \right) \) on \(r=3\cos \theta \). This demonstrates the importance of graphing polar equations when looking for their points of intersection. Since the pole presents particular difficulties, let \(r=0\) in each equation to determine whether the graph passes through the pole.
3 Find the Surface Area of a Solid of Revolution Obtained from a Polar Equation
Suppose a smooth curve \(C\) is given by the polar equation \(r=f(\theta ),\; \alpha \leq \theta \leq \beta \). Parametric equations for this curve are \[ \begin{equation*} x(\theta )=r\cos \theta =f(\theta )\cos \theta \qquad y(\theta )=r\sin \theta =f(\theta )\sin \theta \end{equation*} \]
Then \[ \begin{equation*} \frac{dx}{d\theta }=f' (\theta )\cos \theta -f(\theta )\sin \theta \qquad \frac{dy}{d\theta }=f' ( \theta) \sin \theta +f(\theta )\cos \theta \end{equation*} \] \[ \begin{equation*} \left( \frac{dx}{d\theta }\right) ^{2}+\left( \frac{dy}{d\theta }\right) ^{2}=[ f(\theta )] ^{2}+[ f' ( \theta) ] ^{2}=r^{2}+\left( \dfrac{dr}{d\theta }\right) ^{2} \end{equation*} \]
Since the surface area \(S\) of the solid of revolution obtained by revolving \(C\) about the polar axis (\(x\)-axis) when using parametric equations is \[ \begin{equation*} S=2\pi \int_{\alpha }^{\beta }y( \theta) \sqrt{\left( \dfrac{dx}{ d\theta }\right) ^{2}+\left( \dfrac{dy}{d\theta }\right) ^{2}}d\theta \end{equation*} \]
the surface area \(S\) using a polar equation is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { S=2\pi \int_{\alpha }^{\beta }r\sin \theta \sqrt{ r^{2}+\left( \dfrac{dr}{d\theta }\right) ^{2}}d\theta =2\pi \int_{\alpha }^{\beta }f(\theta )\sin \theta \sqrt{[ f(\theta )] ^{2}+[ f' ( \theta) ] ^{2}}~d\theta }}\tag{1} \]
Finding the Surface Area of a Solid of Revolution
Find the surface area of the solid of revolution generated by revolving the arc of the circle \(r=a,\) \(a>0,\) \(0\leq \theta \leq \dfrac{\pi }{4}\), about the polar axis.
Solution See Figure 55. We find the surface area \(S\) using formula (1). Since \(r=f(\theta )=a,\;f' ( \theta) =0.\) Then \[ \begin{eqnarray*} S& =&2\pi \int_{\alpha }^{\beta }f(\theta )\sin \theta \sqrt{[ f(\theta )] ^{2}+[ f' ( \theta) ] ^{2}}~d\theta\\[4pt] &=&2\pi \int_{0}^{\pi /4}a\sin \theta \sqrt{a^{2}}\,d\theta =2\pi a^{2}\int_{0}^{\pi /4}\sin \theta \,d\theta \notag \\[4pt] & =&2\pi a^{2}\big[ -\cos \theta \big] _{0}^{\pi /4}=2\pi a^{2}\left( -\frac{\sqrt{2}}{2}+1\right) =\pi a^{2}( 2-\sqrt{2}) \end{eqnarray*} \]

NOW WORK
Problem 27.