9.7 The Polar Equation of a Conic
OBJECTIVES
When you finish this section, you should be able to:
- Express a conic as a polar equation (p. 686)
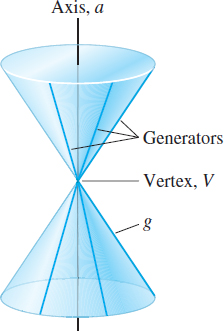
The polar equation of a conic is used to explain and to derive Kepler’s Laws of Planetary Motion, which are discussed in Chapter 11. The word “conic” is derived from the word “cone,” which is a geometric figure that can be constructed in the following way: Let \(a\) and \(g\) be two distinct lines that intersect at a point \(V.\) Fix the line \(a\) and revolve the line \(g\) about \(a\) while keeping the angle between the lines constant. The collection of points swept out by the line \(g\) is called a right circular cone. See Figure 56. The fixed line \(a\) is called the axis of the cone; the point \(V\) is its vertex. Any line passing through \(V\) that makes the same angle with \(a\) as the original line \(g\) is called a generator of the cone. Each generator lies entirely on the cone. The cone consists of two parts, called nappes, that intersect at the vertex.
685
Conics, an abbreviation for conic sections, are curves that result when a right circular cone and a plane intersect. The conics discussed here arise when the plane does not contain the vertex of the cone, as shown in Figure 57. If the plane contains the vertex, the intersection of the plane and the cone is a point, a line, or a pair of lines. These are called degenerate cases.
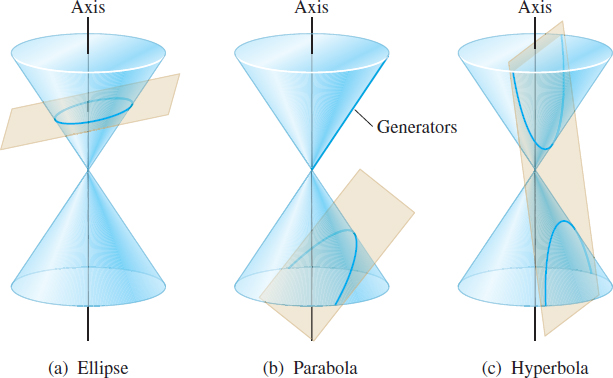
A conic is:
- an ellipse, when the plane intersects the axis \(a\) at an angle greater than the angle between \(a\) and \(g\). An ellipse lies on only one nappe of the cone. See Figure 57(a).
- a parabola, when the plane intersects the axis \(a\) at the same angle as the line \(g;\) that is, the plane is parallel to exactly one generator. A parabola lies on only one nappe of the cone. See Figure 57(b).
- a hyperbola, when the plane intersects the axis \(a\) at an angle smaller than the angle between \(a\) and \(g.\) A hyperbola lies on both nappes of the cone. See Figure 57(c).
In Appendix A.3, pp. A-22 to A-25, we discuss the rectangular equations of a parabola, an ellipse, and a hyperbola. To obtain the polar equations, we use a unified definition that simultaneously defines all three conics.
spanDEFINITIONspan
Let \(D\) denote a fixed line called the directrix; let \(F\) denote a fixed point called the focus, which is not on \(D;\) and let \(e\) be a fixed positive number called the eccentricity. A conic is the set of points \(P\) in the plane for which the ratio of the distance from \(F\) to \(P\) to the distance from \(D\) to \(P\) equals \(e.\) That is, a conic is the collection of points \(P\) for which \[ \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \dfrac{d( F,P) }{d( D,P) }=e \tag{1} }} \end{equation*} \]
- If \(e=1,\) the conic is a parabola.
- If \(e<1,\) the conic is an ellipse.
- If \(e>1\), the conic is a hyperbola.
Figure 58 illustrates the definition.
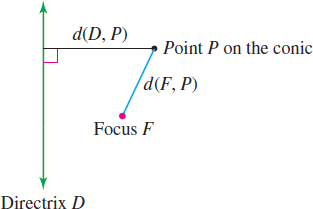
- In a parabola, the axis is the line through the focus perpendicular to the directrix.
- In an ellipse, the major axis is the line through the focus perpendicular to the directrix.
- In a hyperbola, the transverse axis is the line through the focus perpendicular to the directrix.
1 Express a Conic as a Polar Equation
686
The equations for the conics in polar coordinates are derived by positioning the focus \(F\) at the pole (the origin) and the directrix \(D\) either parallel to or perpendicular to the polar axis.
Suppose the directrix \(D\) is perpendicular to the polar axis at a distance \(p\) units to the left of the pole (the focus \(F\)), as shown in Figure 59. If \(P=( r,\theta)\) is any point on the conic, then by (1),
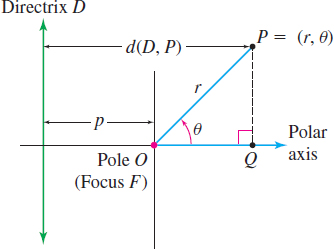
\[ \begin{equation*} \dfrac{d( F,P) }{d( D,P) }=e\qquad \hbox{or}\qquad d(F,P) =e\cdot d( D,P) \end{equation*} \]
Now drop the perpendicular from the point \(P\) to the polar axis. Using the point of intersection \(Q\), we have \(d(O,Q) =r\cos \theta.\) Then \[ \begin{equation*} d( D,P) =p+d( O,Q) =p+r\cos \theta \end{equation*} \]
Since \(d( F,P) =d( O,P) =r,\) \[ \begin{eqnarray*} d( F,P) &=&e\cdot d( D,P) \\ r &=&e( p+r\cos \theta) &&\quad {\color{#0066A7}{{\hbox{\(d(F,P) =r; d(D,P) =p+r \cos \theta\)}}}} \\ r-er\cos \theta &=&ep \\ r &=&\dfrac{ep}{1-e\cos \theta } \end{eqnarray*} \]
The Polar Equation of a Conic
The polar equation of a conic with focus at the pole and directrix perpendicular to the polar axis at a distance \(p\) to the left of the pole is \[ \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ r=\dfrac{ep}{1-e\cos \theta }}} \tag{2} \end{equation*} \]
where \(e\) is the eccentricity of the conic.

Identifying and Graphing the Polar Equation of a Conic
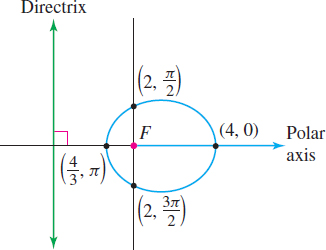
(a) Identify and graph the equation \(r=\dfrac{4}{2-\cos \theta }\).
(b) Convert the polar equation to a rectangular equation.
(c) Find parametric equations for the polar equation.
Solution (a) We divide the numerator and the denominator by \(2\) to express the equation in the form \(r=\dfrac{ep}{1-e\cos \theta }.\) \[ r=\dfrac{4}{2-\cos \theta }=\dfrac{2}{1-\dfrac{1}{2}\cos \theta }\quad\quad {\color{#0066A7}{\hbox{\(r=\dfrac{ep}{1-e\cos \theta}\)}}} \]
Now we see that \(e=\dfrac{1}{2}.\) Since \(ep=2,\) we find \(p=\dfrac{2}{e}=\dfrac{2}{\dfrac{1}{2}}=4.\) This is an ellipse, because \(e=\dfrac{1}{2}<1.\) One focus is at the pole, and the directrix is perpendicular to the polar axis a distance of \(p=4\) units to the left of the pole. The major axis is along the polar axis.
Letting \(\theta =0\) and \(\theta =\pi ,\) we can find the vertices of the ellipse. \[ \begin{equation*} r=\dfrac{4}{2-\cos 0}=\dfrac{4}{2-1}=4\qquad\hbox{and}\qquad r=\dfrac{4}{2-\cos \pi }=\dfrac{4}{2-\left( -1\right) }=\dfrac{4}{3} \end{equation*} \]
687
So, the vertices of the ellipse are the points whose polar coordinates are \(\left( 4,0\right)\) and \(\left( \dfrac{4}{3},\pi \right).\) The y-intercepts of the ellipse are at \(\theta=\dfrac{\pi}{2}\) and \(\theta= \dfrac{3\pi}{2}\), which give rise to the points \(\left(2,\dfrac{\pi}{2}\right)\) and \(\left(2,\dfrac{3\pi}{2}\right)\). The graph of the ellipse is shown in Figure 60.
(b) To obtain a rectangular equation of the ellipse, we eliminate the fraction and then square the resulting polar equation. \[ \begin{array}{rcl@{\qquad}l} r &=& \dfrac{4}{2-\cos \theta}\\ r\left( 2-\cos \theta \right) &=&4\\ 2r-r\cos \theta &=&4\\ 2r &=&4+r\cos \theta\\ 4r^{2} &=&\left( 4+r\cos \theta \right) ^{2} & {\color{#0066A7}{{\hbox{Square the equation.}}}} \\ 4( x^{2}+y^{2}) &=&( 4+x) ^{2} & {\color{#0066A7}{{\hbox{\(r^{2}=x^{2}+y^{2},\; x=r\cos \theta\)}}}} \\ 4x^{2}+4y^{2} &=&16+8x+x^{2} \\ 3\left( x^{2}-\dfrac{8}{3}x\right)+4y^{2} &=&16 \\ 3\left( x-\dfrac{4}{3}\right) ^{2}+4y^{2} &=&16+3\left( \dfrac{16}{9}\right) =\dfrac{64}{3} & {\color{#0066A7}{{\hbox{Complete the square in \(x\).}}}} \end{array} \]
This is the equation of an ellipse in rectangular coordinates, with its center at the point \(\left( \dfrac{4}{3},0\right)\) in rectangular coordinates.
(c) Parametric equations of the ellipse \(r=\dfrac{4}{2-\cos\theta }\) are \[ \begin{equation*} x( \theta) =r\cos \theta =\dfrac{4 \cos \theta }{2-\cos \theta }\qquad y( \theta) =r\sin \theta =\dfrac{4 \sin \theta }{2-\cos \theta }\;0\leq \theta \leq 2\pi \end{equation*} \] where \(\theta\) is the parameter.
There are four possibilities for the position of the directrix relative to the polar axis. These are summarized in Table 8.
| Equation | Description |
|---|---|
| \(r=\dfrac{ep}{1-e\cos \theta }\) | Directrix is perpendicular to the polar axis a distance \(p\) units to the left of the pole. |
| \(r=\dfrac{ep}{1+e\cos \theta }\) | Directrix is perpendicular to the polar axis a distance \(p\) units to the right of the pole. |
| \(r=\dfrac{ep}{1+e\sin \theta }\) | Directrix is parallel to the polar axis a distance \(p\) units above the pole. |
| \(r=\dfrac{ep}{1-e\sin \theta }\) | Directrix is parallel to the polar axis a distance \(p\) units below the pole. |
| Eccentricity | |
|---|---|
| If \(e=1,\) the conic is a parabola; the axis of symmetry is perpendicular to the directrix. | |
| If \(e<1,\) the conic is an ellipse; the major axis perpendicular to the directrix. | |
| If \(e>1,\) the conic is a hyperbola; the transverse axis is perpendicular to the directrix. | |
NOW WORK
Problems 5 and 13.
688
Analyzing the Orbit of an Exoplanet
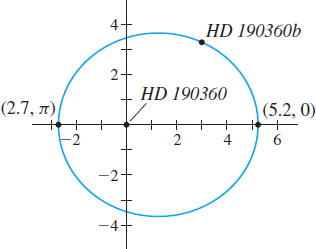
Many hundreds of planets beyond our solar system have been discovered. They are known as exoplanets. One of these exoplanets, HD 190360b, orbits the star HD 190360 (most stars do not have names) in an elliptical orbit given by the polar equation \[ r=\dfrac{3.575}{1-0.316 \cos \theta } \] where the star HD 190360 is at the pole, the major axis is along the polar axis, and \(r\) is measured in astronomical units (AU). (One AU \(=1.5\times 10^{11} {m},\) which is the average distance from Earth to the Sun.)
(a) What is the eccentricity of the exoplanet HD 190360b’s orbit?
(b) Find the distance from the exoplanet HD 190360b to the star HD 190360 at periapsis (shortest distance).
(c) Find the distance from the exoplanet HD 190360b to the star HD 190360 at apoapsis (greatest distance).
Solution (a) The equation of HD 190360b’s orbit is in the form \(r=\dfrac{ep}{1-e\cos \theta }.\) So, the eccentricity of the orbit is \(e=0.316.\) See Figure 61.
(b) Periapsis occurs when \(r\) is a minimum. Since \(r\) is minimum when \(\cos \theta =-1,\) periapsis occurs for \[ \begin{equation*} r=\dfrac{3.575}{1-0.316 \cos \theta }=\dfrac{3.575}{1-0.316( -1) }= \dfrac{3.575}{1.316}\approx 2.717 \end{equation*} \]
The periapsis is at the point \(( 2.717,\pi ) .\) The exoplanet HD 190360b is approximately \(2.717\) AU from the star HD 190360 at periapsis.
(c) The apoapsis occurs when \(r\) is a maximum. Since \(r\) is maximum when \(\cos \theta =1,\) the apoapsis occurs for \[ r=\dfrac{3.575}{ 1-0.316 \cos \theta}=\dfrac{3.575}{1-0.316(1) }=\dfrac{3.575}{0.684} \approx 5.227 \]
The apoapsis is at the point \(( 5.227,0)\). The exoplanet HD 190360b is approximately \(5.227\) AU from the star HD 190360 at apoapsis.
NOW WORK
Problem 33.