CHAPTER 9 PROJECT Polar Graphs and Microphones

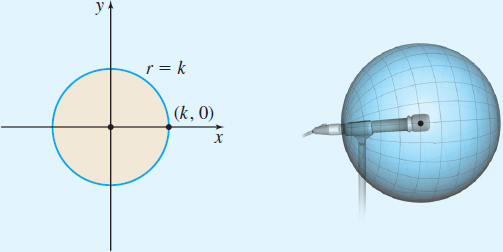
Microphones can be configured to have different sensitivities which are best modeled using various polar patterns. The oldest example is an omnidirectional microphone which records sound equally from all directions. Omnidirectional microphones can be a good option when recording jungle sounds or general ambient noise, or when recording for your cell phone. The recording pattern for this microphone is virtually circular, and a good polar model is \[r=k\]

where \(k>0\) is the sensitivity parameter. Notice that by adjusting \(k\) (say using \(1,4,\) or \(8\)) we obtain concentric circles. Rotating any one of these circles around a diameter results in a sphere. Notice that the microphone receiver is at the center of the sphere and that sound from all directions is received equally.

For this model, say when \(k=1\), we can convert the polar equation to parametric equations obtaining \[ x=\cos t\quad y=\sin t\quad 0\leq t\leq 2\pi \]

Sound technicians have several things to consider when using microphones, including finding the best location to place the microphone and the best location to place any monitors. Since an omnidirectional microphone collects sound equally from all directions, the microphone should be placed directly in the center of the sounds being recorded with the most important sounds positioned closest to the microphone. Unfortunately, monitors cannot be used with an omnidirectional microphone since there is no place to put them where the microphone does not pick up their sound. To help remedy this and other possible issues, different types of microphone models are used.

A cardioid microphone is used when we want to pick up sounds mostly from the front of the microphone. Cardioid microphones are considered “unidirectional”. A polar model for a cardioid microphone is \[ r=k( 1+\cos \theta )\quad 0\leq \theta \leq 2\pi\quad k>0 \]

Notice that the microphone is placed with the transducer at the pole and pointing toward the polar axis. A cardioid microphone is formed by rotating the cardioid about the polar axis. See the figure.

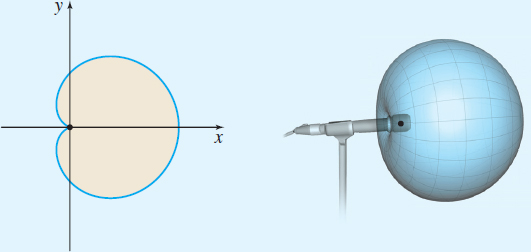
1. Sketch several cardioids using \(k=1,4, 8\).
2. Explain why any noise created by the person's hand or the microphone stand is unlikely to be picked up by a cardioid microphone.
3. Using \(k=1\), convert the cardioid polar equation to a pair of parametric equations.
4. To determine the percentage of the sound that comes from the “front” of the microphone, we consider the sound coming at the microphone with angles in the polar wedge \(-\dfrac{\pi }{4}\leq \theta \leq \dfrac{\pi }{4}\). With \(k=1\), determine the proportion of the surface area coming in from the front relative to that coming in from all directions.
5. Determine the proportion of the sound that is picked up from behind the microphone in the polar wedge \(\dfrac{3\pi }{4}\leq \theta \leq \dfrac{5\pi }{4}\).

   Since less than \(1\%\) of all the sound received comes from the backside of a cardioid microphone, monitors can be placed directly behind the microphone.

   A hypercardioid microphone is used to pick up sounds mostly from in front of the microphone, but it also receives some sound from the rear. A polar model for such a hypercardioid microphone is \[ r=\dfrac{k\,|\,1+2\cos \theta \text{ }|}{3}\quad 0\leq \theta \leq 2\pi\quad k>0 \]

   

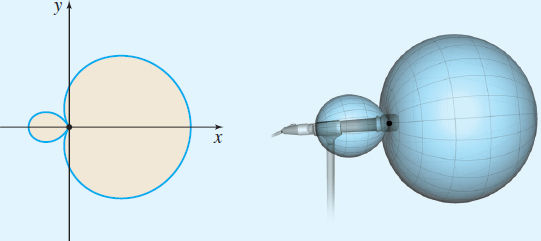
6. Sketch several hypercardioid graphs using \(k=1,\;4,\) and \(8\).
7. Express the hypercardioid polar equation with \(k=1,\) as a pair of parametric equations.
8. Determine the proportion of the sound that is picked up from the front of a hypercardioid microphone \(r=\dfrac{|\,1+2\cos \theta |}{3}\) by finding percentage of sound coming at the microphone from the polar wedge \(-\dfrac{\pi }{4}\leq \theta \leq \dfrac{\pi }{4}\).
9. Determine the proportion of the sound that is picked up from behind the hypercardioid microphone in the polar wedge \(\dfrac{3\pi}{4}\leq \theta \leq \dfrac{5\pi }{4}\).
10. Compare the results of Problems 4, 5, 8, and 9, and describe how the microphones differ.