OBJECTIVES

When you finish this section, you should be able to:

1. Find an equation of the tangent line at a point on a plane curve (p. 648)
2. Find the arc length of a plane curve (p. 651)

spanDEFINITIONspan Smooth Curve

Let \(C\) denote a plane curve represented by the parametric equations \[ \begin{equation*} x=x\,(t)\qquad y=y(t)\quad a\leq t\leq b \end{equation*} \]

Suppose each function \(x(t)\) and \(y(t)\) is continuous on the closed interval \([ a,b] \) and differentiable on the open interval \(( a,b)\). If both \(\dfrac{dx}{dt}\) and \(\dfrac{dy}{dt}\) are continuous and are never simultaneously \(0\) on \(( a,b) \), then \(C\) is called a smooth curve.

THEOREM Slope of the Tangent Line to a Smooth Curve

For a smooth curve \(C\) represented by the parametric equations \(x=x(t),\) \(y=y(t),\) \( a\leq t\leq b\), the slope of the tangent line to \(C\) at the point \(( x, y) \) is given by \[ \begin{equation*}{ \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}} }}\tag{1} } \end{equation*} \]

provided \(\dfrac{dx}{dt}\neq 0\).

NEED TO REVIEW?

Equations of tangent lines are discussed in Section 2.1, pp. 147-149.

Finding an Equation of the Tangent Line to a Smooth Curve

(a) Find an equation of the tangent line to the plane curve with parametric equations \(x(t) =3t^{2},\quad y(t) =2t\), when \(t=1\).

(b) Find all the points on the plane curve at which the tangent line is vertical.

Solution (a) The curve is smooth \(\bigg(\dfrac{{\it dy}}{{\it dt}}=2 {\rm \, is \, never \, zero} \bigg)\). Since \(\dfrac{dx}{dt}=6t\) is not 0 at \(t=1\), the slope of the tangent line to the curve is \[ \begin{equation*} \frac{dy}{dx}=\frac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\frac{\dfrac{d}{dt} ( 2t) }{\dfrac{d}{dt}\left( 3t^{2}\right) }=\dfrac{2}{6t}=\frac{1 }{3t} \end{equation*} \]

When \(t=1\), the slope of the tangent line is \(\dfrac{1}{3}\). Since \(x=3\) and \(y=2\) when \(t=1\), an equation of the tangent line is \[ \begin{array}{rcl@{\qquad\qquad}l} y-2 &=&\dfrac{1}{3} ( x-3 ) & {\color{#0066A7}{{y-y_{1} =m( x-x_{1});}}\;{\color{#0066A7}{ x_{1} =3, y_{1} =2, m= \dfrac{1}{3}}}} \\ y &=&\dfrac{1}{3}x+1 \end{array} \]

Figure 13 \(x(t)=3t^2,\quad y(t) = 2t\)

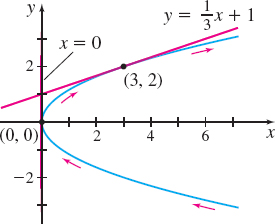
(b) A vertical tangent line occurs when \(\dfrac{dx}{dt}=0\) and \( \dfrac{dy}{dt}\neq 0.\) Since \(\dfrac{dx}{dt}=0\) and \(\dfrac{dy}{ dt}=2\) when \(t=0,\) there is a vertical tangent line to the curve when \(t=0,\) namely at the point \((0,0)\).

NOW WORK

Problem 15.

Finding the Slope of the Tangent Line to a Cycloid

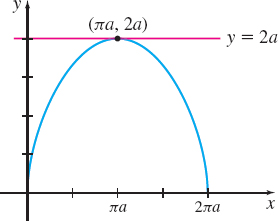
Consider the cycloid defined by \[ \begin{equation*} x(t) =a(t-\sin t)\qquad y(t) =a(1-\cos t)\qquad 0<t<2\pi \qquad a>0 \end{equation*} \]

(a) Show that the slope of the tangent line to the cycloid is given by \(\dfrac{\sin t}{1-\cos t}\).

(b) Find any points where the tangent line to the cycloid is horizontal.

Solution (a) \[ \begin{align*} x(t)&=at-a\sin t& y(t)=a-a\cos t \\ \dfrac{dx}{dt}&=a-a\cos t&\dfrac{dy}{dt}=a\sin t \end{align*} \]

Figure 14 \(x(t)=a(t-\sin t),\\ y(t)=a(1-\cos t),\\ 0< t < 2\pi\)

For \(0<t<2\pi, {\dfrac{dx}{dt}} = a(1-\cos t) \neq 0\). Then the slope of the tangent line is \[ \begin{equation*} \frac{dy}{dx}=\frac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\frac{a\sin t}{a(1-cost)}=\frac{\sin t}{1-\cos t} \end{equation*} \]

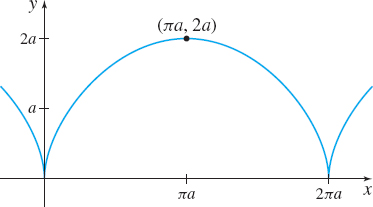
(b) The cycloid has a horizontal tangent line when \(\dfrac{dy}{dt} =a\sin t=0,\) but \(\dfrac{dx}{dt}\neq 0.\) For \(0<t<2\pi\), we have \(a\sin t=0\) when \(t=\pi\). Since \(\dfrac{dx}{dt}\neq 0\) for \(0< t< 2\pi ,\) the cycloid has a horizontal tangent line when \(t=\pi ,\) at the point \((\pi a,2a)\). The equation of the horizontal tangent line is \(y=2a\), as shown in Figure 14.

NOW WORK

Problem 27.

Finding an Equation of the Tangent Line to a Smooth Curve

Figure 15 \(x(t)=t^3-4t,\quad y(t)=t^2\)

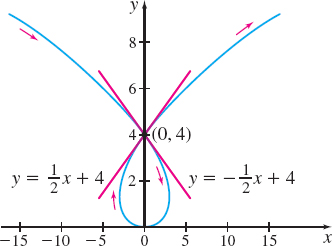
The plane curve represented by the parametric equations \(x(t)=t^{3}-4t,\quad y(t) =t^{2}\), crosses itself at the point \((0,4)\), and so has two tangent lines there, as shown in Figure 15. Find equations for these tangent lines.

Solution We begin by finding the numbers \(t\) that correspond to the point \(( 0,4) .\) \[ \begin{array}{rcl@{\quad\qquad}lrll} x &=&0 & y&=&4 \\ t^{3}-4t &=&0 & t^{2}&=&4 \\ t( t^{2}-4) &=& 0 & t&=&-2\hbox{ or }2 \\ t &=&0,-2,\hbox{or }2 & \end{array} \]

We exclude \(t=0,\) since if \(t=0,\) then \(y\neq 4.\) So we investigate only \( t=-2\) and \(t=2.\) Since \(\dfrac{dx}{dt}=3t^{2}-4\neq 0\) for \(t=-2\) and \(t=2,\) the slope of the tangent lines is given by \[ \begin{equation*} \frac{dy}{dx}=\frac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\frac{\dfrac{d}{dt} ( t^{2}) }{\dfrac{d}{dt}( t^{3}-4t) }=\dfrac{2t}{ 3t^{2}-4} \end{equation*} \]

When \(t=-2\), the slope of the tangent line is \[ \begin{equation*} \dfrac{dy}{dx}=\dfrac{2( -2) }{3( -2) ^{2}-4}=\dfrac{-4 }{8}=-\dfrac{1}{2} \end{equation*} \]

and an equation of the tangent line at the point \(( 0,4) \) is \[ \begin{eqnarray*} y-4 &=&-\dfrac{1}{2}( x-0) \\ y &=&-\dfrac{1}{2}x+4 \end{eqnarray*} \]

When \(t=2\), the slope of the tangent line at the point \(( 0,4) \) is \[ \begin{equation*} \dfrac{dy}{dx}=\dfrac{2( 2) }{3( 2) ^{2}-4}=\dfrac{4}{8 }=\dfrac{1}{2} \end{equation*} \]

and an equation of the tangent line at \(( 0,4) \) is \[ \begin{eqnarray*} y-4 &=&\dfrac{1}{2}( x-0) \\ y &=&\dfrac{1}{2}x+4 \end{eqnarray*} \]

NOW WORK

Problem 45.

Projectile Motion

A projectile is fired at an angle \(\theta ,\) \(0<\theta <\dfrac{\pi }{2},\) to the horizontal with an initial speed of \(v_{0}\) m/s. Assuming no air resistance, the position of the projectile after \(t\) seconds is given by the parametric equations \(x(t) =( v_{0}\cos \theta ) t,\) \(y(t) =( v_{0}\sin \theta ) t-\dfrac{1}{2} gt^{2},\quad t\geq 0,\) where \(g\) is the acceleration due to gravity.

(a) Find the slope of the tangent line to the motion of the projectile as a function of \(t\).

(b) At what time is the projectile at its maximum height?

Solution (a) The slope of the tangent line is given by \(\dfrac{dy }{dx}.\) \[ \begin{equation*} \dfrac{dy}{dx}=\frac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\dfrac{\dfrac{d}{ dt}\left[ \left( v_{0}\sin \theta \right) t-\dfrac{1}{2}gt^{2}\right] }{ \dfrac{d}{dt}\left[ \left( v_{0}\cos \theta \right) t\right] }=\dfrac{ v_{0}\sin \theta -gt}{v_{0}\cos \theta }=\tan \theta -\dfrac{gt}{v_{0}\cos \theta } \end{equation*} \]

(b) The projectile is at its maximum height when the slope of the tangent line equals \(0.\) That is, when \[ \begin{eqnarray*} \dfrac{dy}{dx} =\dfrac{v_{0}\sin \theta -gt}{v_{0}\cos \theta } &=& 0 \notag\\ v_{0}\sin \theta -gt &=&0 \notag \\ t &=&\dfrac{v_{0}\sin \theta }{g} \end{eqnarray*} \]

NEED TO REVIEW?

Arc length is discussed in Section 6.5, pp. 438-442.

THEOREM Arc Length Formula for Parametric Equations

For a smooth curve \(C\) represented by the parametric equations \[ x=x(t)\qquad y=y(t)\quad a\leq t\leq b \]

the arc length \(s\) of \(C\) from \(t=a\) to \(t=b\) is given by the formula \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ s=\int_{a}^{b}\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}~dt }} \]

Finding Arc Length for Parametric Equations

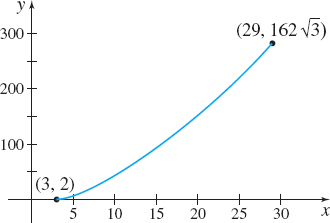
Find the length \(s\) of the curve represented by the parametric equations \[ \begin{equation*} x(t) =t^{3}+2\qquad\hbox{}\qquad y(t) =2t^{9/2} \end{equation*} \]

from the point where \(t=1\) to the point where \(t=3\). Figure 16 shows the graph of the curve.

Figure 16 \(x(t) =t^{3}+2,\) \(y(t) =2t^{9/2},\) \(1\leq t\leq 3\)

Solution We begin by finding the derivatives \(\dfrac{dx}{dt}\) and \(\dfrac{dy}{dt}.\) \[ \begin{equation*} \dfrac{dx}{dt}=3t^{2}\qquad\hbox{and}\qquad \dfrac{dy}{dt}=9t^{7/2} \end{equation*} \]

The curve is smooth for \(1\leq t\leq 3.\) Now using the arc length formula for parametric equations, we have \[ \begin{eqnarray*} s&=&\int_{a}^{b}\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt} \right) ^{2}}~dt=\int_{1}^{3}\sqrt{(3t^{2})^{2}+(9t^{7/2})^{2}} \,dt\\[6pt] &=&\int_{1}^{3}\sqrt{9t^{4}+81\,t^{7}}\,dt =\int_{1}^{3}3t^{2}\sqrt{1+9t^{3} }\,dt \end{eqnarray*} \]

We use the substitution \(u=1+9t^{3}\). Then \(du=27t^{2}dt,\) or equivalently, \(3t^{2}dt=\dfrac{du}{9}.\) Changing the limits of integration, we find that when \(t=1,\) then \(u=10;\) and when \(t=3,\) then \(u=1+9\cdot 3^{3}=244.\) The arc length \(s\) is \[ \begin{eqnarray*} s&=&\int_{1}^{3}3t^{2}\sqrt{1+9t^{3}}\,dt=\int_{10}^{244}\sqrt{u}\left( \frac{ du}{9}\right) =\dfrac{1}{9}\int_{10}^{244}u^{1/2}du=\frac{1}{9}\left[ \frac{ u^{3/2}}{\dfrac{3}{2}}\right] _{10}^{244}\\ &=&\frac{2}{27}[244^{3/2}-10^{3/2}] = \frac{4}{27}\big[244\sqrt{61}- 5\sqrt{10}\big] \end{eqnarray*} \]

NOW WORK

Problem 31.

Finding the Arc Length of a Cycloid

Find the length \(s\) of one arch of the cycloid: \[ \begin{equation*} x(t) =a(t-\sin t)\qquad y(t) =a(1-\cos t)\quad a>0 \end{equation*} \]

Figure 17 shows the graph of the cycloid.

Figure 17 \(x(t) =a(t-\sin t)\), \(y(t) =a(1-\cos t),\quad a>0\).

Solution One arch of the cycloid is obtained when \(t\) varies from \(0\) to \(2\pi .\) Since \[ \begin{equation*} \dfrac{dx}{dt}=a-a\cos t=a(1-\cos t)\qquad\hbox{and}\qquad \dfrac{dy}{dt}=a\sin t \end{equation*} \]

are both continuous and are never simultaneously \(0\) on \(( 0,2\pi) \), the cycloid is smooth on \([ 0,2\pi ]\). The arc length \(s\) is \[ \begin{eqnarray*} s&=&\int_{a}^{b}\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt} \right) ^{2}}~dt=\int_{0}^{2\pi } \sqrt{a^{2}(1-\cos t)^{2}+a^{2}\sin ^{2}t} \\ &=&a \int^{2\pi}_0 \sqrt{( 1-2\cos t+\cos ^{2}t) +\sin ^{2}t} ~dt = a \int^{2\pi}_0 \sqrt{1-2\cos t+1}~dt\\ &=& \sqrt{2} a \int^{2\pi}_0 \sqrt{1-\cos t}~dt \end{eqnarray*} \]

To integrate \(\sqrt{1-\cos t}\) we use a half-angle identity. Since \(\sin \dfrac{t}{2}\geq 0\) if \(0\leq t \leq 2\pi ,\) we have \(\sin \dfrac{t}{2}=\sqrt{\dfrac{1-\cos t}{2}}.\) Then \[ \begin{equation*} \sqrt{1-\cos t}=\sqrt{2}\sin \frac{t}{2} \end{equation*} \]

Now the arc length \(s\) from \(t=0\) to \(t=2\pi \) is \[ s= \sqrt{2}a \int_{0}^{2\pi } \sqrt{1 - \cos t}\, dt=\sqrt{2} a \int_{0}^{2\pi }\sqrt{2} \sin \frac{t}{2}~dt=2a\left[ -2\cos \frac{t}{2}\right] _{0}^{2\pi }=8a \]

NOW WORK

Problem 37.

Partial Proof of the Arc Length Formula

The proof for parametric equations is similar to the one we used in Chapter 6 to prove the arc length formula for a function \(y=f( x) ,\) \(a\leq x\leq b.\)

First, we partition the closed interval \([a,b]\) into \(n\) subintervals: \[ \begin{equation*} \lbrack a, t_{1}], [t_{1}, t_{2}], \ldots , [t_{i-1}, t_{i}], \ldots , [t_{n-1},b] \end{equation*} \]

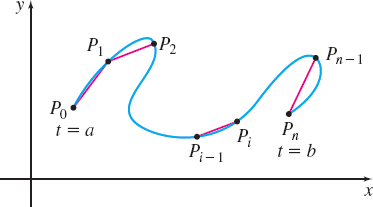
each of length \(\Delta t=\dfrac{b-a}{n}\). Corresponding to each number \( a, t_{1}, t_{2},\ldots ,t_{n-1}, b\), there is a point \(P_{0}, P_{1}, P_{2}, \ldots , P_{n}\), on the curve, as shown in Figure 18.

We join each point \(P_{i-1}\) to the next point \(P_{i}\) with a line segment. The sum of the lengths of the line segments is an approximation to the length of the curve from \(t=a\) to \(t=b\). This sum can be written as \[ \begin{equation*} d(P_{0}, P_{1})+d(P_{1}, P_{2})+\cdots +d(P_{n-1}, P_{n})=\sum_{i=1}^{n}\,d(P_{i-1}, P_{i}) \end{equation*} \]

where \(d(P_{i-1}, P_{i})\) is the length of the line segment joining the points \(P_{i-1}\) and \(P_{i}\). Using the distance formula, the length of each line segment is \(d(P_{i-1}, P_{i})= \sqrt{[ x(t_{i})-x(t_{i-1})] ^{2}+ [ y(t_{i})-y(t_{i-1})] ^{2}}.\) Then the sum of the lengths of the line segments is \[ \sum_{i=1}^{n}\,d(P_{i-1}, P_{i})=\sum_{i=1}^{n}\sqrt{ [x(t_{i})-x(t_{i-1})]^{2}+[y(t_{i})-y(t_{i-1})]^{2}} \]

Since the curve is smooth, the functions \(x=x(t) \) and \(y=y(t) \) satisfy the conditions of the Mean Value Theorem on \([ a,b] ,\) and so satisfy the same conditions on each subinterval \([t_{i-1}, t_{i}]\). This means that there are numbers \(u_{i}\) and \(v_{i}\) in each open interval \( (t_{i-1}, t_{i})\) for which \[ \begin{equation*} x(t_{i})-x(t_{i-1})=\left[ \frac{dx}{dt}(u_{i})\right] \Delta t\qquad y(t_{i})-y(t_{i-1})=\left[ \frac{dy}{dt}(v_{i})\right] \Delta t \end{equation*} \]

The sum of the lengths of the segments can be written as \[ \begin{equation*} \sum_{i=1}^{n}\,d(P_{i-1}, P_{i})=\sum_{i=1}^{n}\sqrt{\left[ \frac{dx}{dt} (u_{i})\right] ^{2}+\left[ \frac{dy}{dt}(v_{i})\right] ^{2}} \Delta t \end{equation*} \]

These sums are not Riemann sums, since the numbers \(u_{i}\) and \(v_{i}\) are not necessarily equal. However, there is a result (usually given in advanced calculus) that states the limit of the sums \(\sum\limits_{i=1}^{n} \sqrt{\left[ \dfrac{dx}{dt}(u_{i})\right] ^{2}+\left[ \dfrac{dy}{dt}(v_{i}) \right] ^{2}\,}\Delta t\), as \(\Delta t\rightarrow 0,\) is a definite integral.* That is, the length \(s\) of the curve from \(t=a\) to \(t=b\) is \[ s=\int_{a}^{b}\sqrt{\left( \frac{dx}{dt}\right) ^{2}+\left( \frac{dy}{dt} \right) ^{2}}~dt \]