9.3 Assess Your Understanding
660
Concepts and Vocabulary
Question
True or False When a smooth curve \(C\) represented by the parametric equations \(x=x(t) ,\) \(y=y(t) ,\) \( y\geq 0,\) \(a\leq t\leq b,\) is revolved about the \(x\)-axis, the surface area \( S\) of the solid of revolution is given by \(S=2\pi \int_{a}^{b}x(t) \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt} \right) ^{2}}dt.\)
Question
The surface area \(S\) of a solid of revolution generated by revolving the smooth curve \(C\) represented by \(x=x(t),\;y=y(t),\;a\leq t\leq b\), where \(x(t)\geq 0\), about the \(y\)-axis is \(S=\) ______________.
Skill Building
In Problems 3–14, find the surface area of the solid generated by revolving each curve about the x-axis.
Question
\(x(t) =3t^{2}, \, y(t) =6t;\;0\leq t\leq 1\)
Question
\(x(t) =t^{2}, \, y(t) =2t;\;0\leq t\leq 3 \)
Question
\(x( \theta) =\cos ^{3}\theta, \, y( \theta) =\sin ^{3}\theta ;\; 0\leq \theta \leq \dfrac{\pi }{2}\)
Question
\(x(t) = t-\sin t, \ \, y(t) = 1-\cos t;\;0\leq t\leq \pi \)
Question
\(y=x^{3},\;0\leq x\leq 1\)
Question
\(y=4x^{3},\;0\leq x\leq 2\)
Question
\(y=\dfrac{x^{4}}{8}+\dfrac{1}{4x^{2}},\;1\leq x\leq 2\)
Question
\(y=\sqrt{x};\;1\leq x\leq 9\)
Question
\(y=e^{x},\;0\leq x\leq 1\)
Question
\(y=e^{-x},\;0\leq x\leq 1\)
Question
\(y= \sqrt{a^{2}-x^{2}},\;-a\leq x\leq a\)
Question
\(y=\dfrac{a}{2}(e^{x/a}+e^{-x/a}),\;0\leq x\leq a\)
In Problems 15–20, find the surface area of the solid generated by revolving each curve about the y-axis.
Question
\(x(t) =3t^{2}, y(t) =2t^{3};\;0\leq t\leq 1\)
Question
\(x(t) =2t+1, \ y(t) =t^{2}+3;\;0\leq t\leq 3\)
Question
\(x(t) =2\sin t, y(t) =2\cos t;\;0\leq t\leq \dfrac{\pi }{2}\)
Question
\(x(t) =3\cos t, y(t) =2\sin t;\;0\leq t\leq \dfrac{\pi }{2} \)
Question
\(x=\dfrac{1}{4}y^{2},\;0\leq y\leq 2\)
Question
\(x^{2/3}+y^{2/3}=a^{2/3};\;x\geq 0, 0\leq y\leq a\)
Question
Find the surface area of the solid generated by revolving one arch of the cycloid \(x(t) =6( t-\sin t) ,\) \(y(t) =6( 1-\cos t) \) about the \(x\) -axis.
Question
![]() Find the surface area of the solid generated by revolving the graph of \(y=\ln x,\) \(1\leq x\leq 10,\) about the \(x\)-axis.
Find the surface area of the solid generated by revolving the graph of \(y=\ln x,\) \(1\leq x\leq 10,\) about the \(x\)-axis.
Applications and Extensions
Question
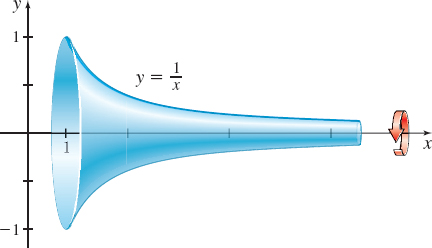
Gabriel’s Horn The surface formed by revolving the region between the graph of \(y=\dfrac{1}{x},\) \(x\geq 1,\) and the \(x\)-axis about the \(x\)-axis is called Gabriel’s horn. See the figure.
- Find the surface area of Gabriel’s horn.
- Find the volume of Gabriel’s horn.
Interesting Note: The volume of Gabriel’s horn is finite, but the surface area of Gabriel’s horn is infinite.
Question
Surface Area Find the surface area of the solid of revolution obtained by revolving the graph of \(y=e^{-x}\), \(x\geq 0\), about the \(x\)-axis.
Question
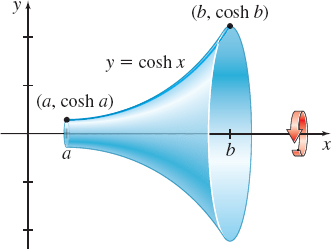
Surface Area of a Catenoid When an arc of a catenary \( y=\cosh x,\) \(a\leq x\leq b\), is revolved about the \(x\)-axis, it generates a surface called a catenoid, which has the least surface area of all surfaces generated by rotating curves having the same endpoints. Find its surface area. See the figure.
Question
Surface Area of a Sphere Find a formula for the surface area of a sphere of radius \(R\).
Question
Surface Area Show that the surface area \(S\) of a right circular cone of altitude \(h\) and radius \(b\) is \(S=\pi b \sqrt{h^{2}+b^{2}}.\)
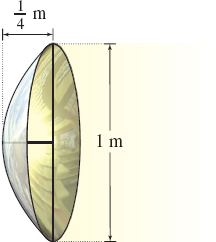
Challenge Problems
Question
Searchlight The reflector of a searchlight is formed by revolving an arc of a parabola about its axis. Find the surface area of the reflector if it measures \(1\) m across its widest point and is \(\dfrac{1 }{4}\) m deep.
661
Question
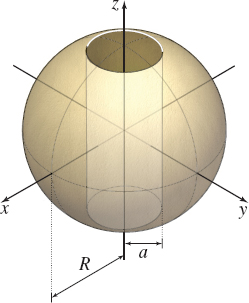
Surface Area of a Bead A sphere of radius \(R\) has a hole of radius \(a<R\) drilled through its center. The axis of the hole coincides with a diameter of the sphere. Find the surface area of the part of the sphere that remains.
Question
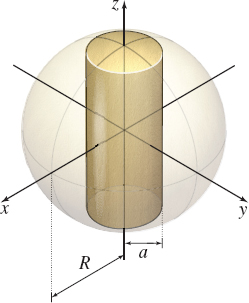
Surface Area of a Plug A plug is made to repair the hole in the sphere in Problem 29. What is the surface area of the plug?