Question

In a polar coordinate system, the origin is called the ______________, and the ______________ coincides with the positive \(x\)-axis of the rectangular coordinate system.

Question

True or False  Another representation in polar coordinates for the point \(\left( 2,\dfrac{\pi }{3}\right)\) is \(\left( 2,\dfrac{4\pi }{3}\right) .\)

Question

True or False  In a polar coordinate system, each point in the plane has exactly one pair of polar coordinates.

Question

True or False  In a rectangular coordinate system, each point in the plane has exactly one pair of rectangular coordinates.

Question

True or False  In polar coordinates \(( r,\theta)\), the number \(r\) can be negative.

Question

True or False  If \(( r,\theta )\) are the polar coordinates of the point \(P,\) then \(\vert r\vert\) is the distance of the point \(P\) from the pole.

Question

To convert the point \(( r,\theta )\) in polar coordinates to a point \(( x,y)\) in rectangular coordinates, use the formulas \(x=\)______________ and \(y=\)______________.

Question

An equation whose variables are polar coordinates is called a(n) ____________________________ .

Question

\(\left( 2,-\dfrac{11\pi }{6}\right)\)

Question

\(\left(-2,-\dfrac{\pi }{6}\right)\)

Question

\(\left( -2,\dfrac{\pi }{6}\right)\)

Question

\(\left( 2,\dfrac{7\pi }{6}\right)\)

Question

\(\left( 2,\dfrac{5\pi }{6}\right)\)

Question

\(\left(-2,\dfrac{5\pi }{6}\right)\)

Question

\(\left( -2,\dfrac{7\pi }{6} \right)\)

Question

\(\left( 2,\dfrac{11\pi }{6}\right)\)

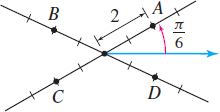
Question

\(\left( 4,\dfrac{\pi }{3}\right)\)

Question

\(\left( -4,\dfrac{\pi }{3}\right)\)

Question

\(\left( -4,-\dfrac{\pi }{3}\right)\)

Question

\(\left( 4,-\dfrac{\pi }{3}\right)\)

Question

\(\left( \sqrt{2},\dfrac{\pi }{4}\right)\)

Question

\(\left( 7,-\dfrac{7\pi }{4}\right)\)

Question

\(\left( -6,\dfrac{4\pi }{3}\right)\)

Question

\(\left( 5,\dfrac{\pi }{2}\right)\)

Question

\(\left( 5,\dfrac{2\pi }{3}\right)\)

Question

\(\left( 4,\dfrac{3\pi }{4}\right)\)

Question

\(( -2,3\pi )\)

Question

\((-3,4\pi )\)

Question

\(\left( 1,\dfrac{\pi }{2}\right)\)

Question

\(( 2,\pi )\)

Question

\(\left( -3,-\dfrac{\pi }{4}\right)\)

Question

\(\left( -2,-\dfrac{2\pi }{3}\right)\)

Question

\(\left( 6,\dfrac{\pi }{6}\right)\)

Question

\(\left( -6,\dfrac{\pi }{6}\right)\)

Question

\(\left( -6,-\dfrac{\pi }{6}\right)\)

Question

\(\left( 6,-\dfrac{\pi }{6}\right)\)

Question

\(\left( 5,\dfrac{\pi }{2}\right)\)

Question

\(\left( 8,\dfrac{\pi }{4}\right)\)

Question

\(\left( 2\sqrt{2},-\dfrac{\pi }{4}\right)\)

Question

\(\left( -5,-\dfrac{\pi }{3}\right)\)

Question

\(( 5,0)\)

Question

\(( 2,-2)\)

Question

\((-2,2)\)

Question

\(( -2,-2\sqrt{3})\)

Question

\(( \sqrt{3},1)\)

Question

\((0,-3)\)

Question

\(( -\sqrt{3},1)\)

Question

\(( 3\sqrt{2},-3\sqrt{2})\)

Question

\(( 3,2)\)

Question

\(( -6.5,1.2)\)

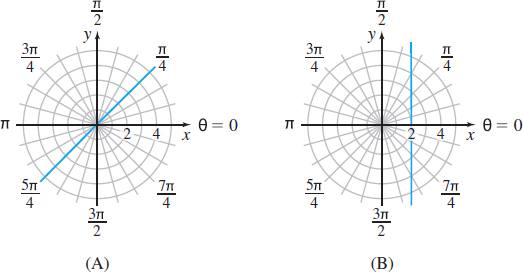
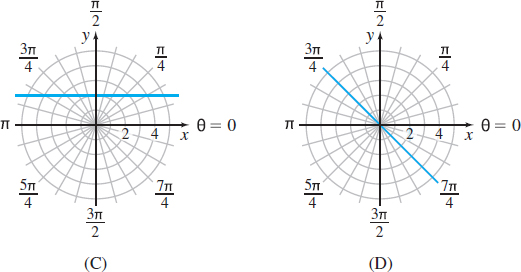
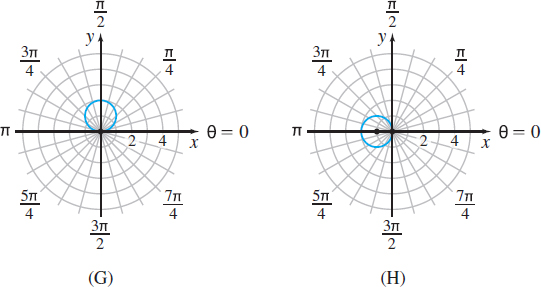
Question

\(r=2\)

Question

\(\theta = \dfrac{\pi }{4}\)

Question

\(r=2\cos \theta\)

Question

\(r\cos \theta =2\)

Question

\(r=-2\cos \theta\)

Question

\(r=2\sin \theta\)

Question

\(\theta =\dfrac{3\pi }{4}\)

Question

\(r\sin \theta =2\)

Question

\(r=4\)

Question

\(r=2\)

Question

\(\theta =\dfrac{\pi }{3}\)

Question

\(\theta =-\dfrac{\pi }{4}\)

Question

\(r\sin \theta =4\)

Question

\(r\cos \theta =4\)

Question

\(r\cos \theta =-2\)

Question

\(r\sin \theta =-2\)

Question

\(r=2\cos \theta\)

Question

\(r=2\sin \theta\)

Question

\(r=-4\sin \theta\)

Question

\(r=-4\cos \theta\)

Question

\(r\sec \theta =4\)

Question

\(r\csc \theta =8\)

Question

\(r\csc \theta =-2\)

Question

\(r\sec \theta =-4\)

Question

\(\dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}=1\)

Question

\(x-4y+4=0\)

Question

\(x^{2}+y^{2}-4x=0\)

Question

\(y=-6\)

Question

\(x^{2}=1-4y\)

Question

\(y^{2}=1-4x\)

Question

\(xy=1\)

Question

\(x^{2}+y^{2}-2x+4y=0\)

Question

\(r=\cos \theta\)

Question

\(r=2+\cos \theta\)

Question

\(r^{2}=\sin \theta\)

Question

\(r^{2}=1-\sin \theta\)

Question

\(r=\dfrac{4}{1-\cos \theta }\)

Question

\(r=\dfrac{3}{3-\cos \theta }\)

Question

\(r^{2}=\theta\)

Question

\(\theta =-\dfrac{\pi }{4}\)

Question

\(r=2\)

Question

\(r=-5\)

Question

\(\tan \theta =4\)

Question

\(\cot \theta =3\)

Question

Chicago In Chicago, the road system is based on a rectangular coordinate system, with the intersection of Madison and State Streets at the origin, and east as the positive \(x\)-axis. Intersections are indicated by the number of blocks they are from the origin. For example, Wrigley Field is located at 1060 West Addison, which is 10 blocks west of State Street and 36 blocks north of Madison Street.

1. Write the location of Wrigley Field using rectangular coordinates.
2. Write the location of Wrigley Field using polar coordinates. Use east as the polar axis.
3. U.S. Cellular Field is located at 35th Street and Princeton, which is 3 blocks west of State Street and 35 blocks south of Madison Street. Write the location of U.S. Cellular Field using rectangular coordinates.
4. Write the location of U.S. Cellular Field using polar coordinates.

Question

Show that the formula for the distance \(d\) between two points \(P_{1}=(r_{1},~\theta _{1})\) and \(P_{2}=(r_{2},~\theta _{2})\) is \[ \begin{equation*} d=\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos (\theta _{2}-\theta _{1})} \end{equation*} \]

Question

Horizontal Line Show that the graph of the equation \(r\sin \theta =a\) is a horizontal line \(a\) units above the pole if \(a>0\), and \(|a|\) units below the pole if \(a<0\).

Question

Vertical Line Show that the graph of the equation \(\ r\cos \theta =a\) is a vertical line \(a\) units to the right of the pole if \(a>0\), and \(|a|\) units to the left of the pole if \(a<0\).

Question

Circle Show that the graph of the equation \(r=2a\sin \theta,\;a>0\), is a circle of radius \(a\) with its center at the rectangular coordinates \((0, a)\).

Question

Circle Show that the graph of the equation \(r=-2a\sin \theta ,\) \(a>0\), is a circle of radius \(a\) with its center at the rectangular coordinates \((0,\,-a)\).

Question

Circle Show that the graph of the equation \(r=2a\cos \theta ,\) \(a>0\), is a circle of radius \(a\) with its center at the rectangular coordinates \((a, 0)\).

Question

Circle Show that the graph of the equation \(r=-2a\cos \theta ,a>0\), is a circle of radius \(a\) with its center at the rectangular coordinates \((-a, 0)\).

Question

Exploring Using Graphing Technology

1. Use a square screen to graph \(r_{1}=\sin \theta ,\) \(r_{2}=2\sin \theta\), and \(r_{3}=3\sin \theta .\)
2. Describe how varying the constant \(a,\) \(a>0,\) alters the graph of \(r=a\sin \theta\).
3. Graph \(r_{1}=-\sin \theta ,\) \(r_{2}=-2\sin \theta ,\) and \(r_{3}=-3\sin \theta .\)
4. Describe how varying the constant \(a,\) \(a<0,\) alters the graph of \(r=a\sin \theta\).

Question

Exploring Using Graphing Technology

1. Use a square screen to graph \(r_{1}=\cos \theta ,\) \(r_{2}=2\cos \theta ,\) and \(r_{3}=3\cos \theta .\)
2. Describe how varying the constant \(a,\) \(a>0,\) alters the graph of \(r=a\cos \theta\).
3. Graph \(r_{1}=-\cos \theta ,\) \(r_{2}=-2\cos \theta ,\) and \(r_{3}=-3\cos \theta .\)
4. Describe how varying the constant \(a,\) \(a<0,\) alters the graph of \(r=a\cos \theta\).

Question

Show that \(r=a\sin \theta +b\cos \theta ,\) \(a,\,b\) not both zero, is the equation of a circle. Find the center and radius of the circle.

Question

Express \(r^{2}=\cos ( 2\theta )\) in rectangular coordinates free of radicals.

Question

Prove that the area of the triangle with vertices \((0,0),~(r_{1},\theta _{1}),(r_{2},\theta _{2})\) is \[ \begin{equation*} A=\dfrac{1}{2}r_{1}r_{2}~\sin (\theta _{2}-\theta _{1})\qquad 0\leq \theta _{1}<\theta _{2}\leq \pi \end{equation*} \]