Contents | Calculus
Preface vi
Applications Index xv
P Preparing for Calculus 1
P.1 Functions and Their Graphs 2
P.2 Library of Functions; Mathematical Modeling 14
P.3 Operations on Functions; Graphing Techniques 24
P.4 Inverse Functions 32
P.5 Exponential and Logarithmic Functions 38
P.6 Trigonometric Functions 49
P.7 Inverse Trigonometric Functions 58
P.8 Technology Used in Calculus 64
1 Limits and Continuity 68
1.1 Limits of Functions Using Numerical and Graphical Techniques 69
1.2 Limits of Functions Using Properties of Limits 81
1.3 Continuity 93
1.4 Limits and Continuity of Trigonometric, Exponential, and Logarithmic Functions 106
1.5 Infinite Limits; Limits at Infinity; Asymptotes 117
1.6 The ɛ–δ Definition of Limit 130
Chapter Review 139
Chapter Project: Pollution in Clear Lake 143
2 The Derivative 144
2.1 Rates of Change and the Derivative 145
2.2 The Derivative as a Function 154
2.3 The Derivative of a Polynomial Function; The Derivative of y = ex 163
2.4 Differentiating the Product and the Quotient of Two Functions; Higher-Order Derivatives 173
2.5 The Derivative of the Trigonometric Functions 185
Chapter Review 192
Chapter Project: The Lunar Module 195
3 More About Derivatives 197
3.1 The Chain Rule 198
3.2 Implicit Differentiation; Derivatives of the Inverse Trigonometric Functions 209
3.3 Derivatives of Logarithmic Functions 222
3.4 Differentials; Linear Approximations; Newton’s Method 230
3.5 Taylor Polynomials 240
3.6 Hyperbolic Functions 243
Chapter Review 250
Chapter Project: World Population 253
4 Applications of the Derivative 254
4.1 Related Rates 255
4.2 Maximum and Minimum Values; Critical Numbers 263
4.3 The Mean Value Theorem 275
4.4 Local Extrema and Concavity 284
4.5 Indeterminate Forms and L’Hôpital’s Rule 298
4.6 Using Calculus to Graph Functions 308
4.7 Optimization 318
4.8 Antiderivatives; Differential Equations 328
Chapter Review 338
Chapter Project: The U.S. Economy 342
5 The Integral 343
5.1 Area 344
5.2 The Definite Integral 353
5.3 The Fundamental Theorem of Calculus 362
5.4 Properties of the Definite Integral 369
5.5 The Indefinite Integral; Growth and Decay Models 379
5.6 Method of Substitution; Newton’s Law of Cooling 387
Chapter Review 400
Chapter Project: Managing the Klamath River 403
6 Applications of the Integral 404
6.1 Area Between Graphs 405
6.2 Volume of a Solid of Revolution: Disks and Washers 413
6.3 Volume of a Solid of Revolution: Cylindrical Shells 424
6.4 Volume of a Solid: Slicing Method 433
6.5 Arc Length 438
6.6 Work 444
6.7 Hydrostatic Pressure and Force 453
6.8 Center of Mass; Centroid; The Pappus Theorem 458
Chapter Review 467
Chapter Project: Determining the Amount of Concrete Needed for a Cooling Tower 469
7 Techniques of Integration 471
7.1 Integration by Parts 472
7.2 Integrals Containing Trigonometric Functions 480
7.3 Integration Using Trigonometric Substitution: Integrands Containing
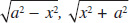, or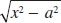 
, a > 0 4887.4 Substitution: Integrands Containing ax2 + bx + c 496
7.5 Integration of Rational Functions Using Partial Fractions 499
7.6 Integration Using Numerical Techniques 508
7.7 Integration Using Tables and Computer Algebra Systems 520
7.8 Improper Integrals 523
Chapter Review 533
Chapter Project: The Birds of Rügen Island 535
8 Infinite Series 537
8.1 Sequences 538
8.2 Infinite Series 553
8.3 Properties of Series; the Integral Test 566
8.4 Comparison Tests 575
8.5 Alternating Series; Absolute Convergence 582
8.6 Ratio Test; Root Test 591
8.7 Summary of Tests 596
8.8 Power Series 600
8.9 Taylor Series; Maclaurin Series 611
8.10 Approximations Using Taylor/Maclaurin Expansions 623
Chapter Review 630
Chapter Project: How Calculators Calculate 634
9 Parametric Equations; Polar Equations 636
9.1 Parametric Equations 637
9.2 Tangent Lines; Arc Length 647
9.3 Surface Area of a Solid of Revolution 656
9.4 Polar Coordinates 661
9.5 Polar Equations; Parametric Equations of Polar Equations; Arc Length of Polar Equations 670
9.6 Area in Polar Coordinates 678
9.7 The Polar Equation of a Conic 684
Chapter Review 690
Chapter Project: Polar Graphs and Microphones 692
10 Vectors; Lines, Planes, and Quadric Surfaces in Space 694
10.1 Rectangular Coordinates in Space 695
10.2 Introduction to Vectors 699
10.3 Vectors in the Plane and in Space 703
10.4 The Dot Product 715
10.5 The Cross Product 724
10.6 Equations of Lines and Planes in Space 733
10.7 Quadric Surfaces 744
Chapter Review 752
Chapter Project: The Hall Effect 755
11 Vector Functions 757
11.1 Vector Functions and Their Derivatives 758
11.2 Unit Tangent and Principal Unit Normal Vectors; Arc Length 767
11.3 Arc Length as Parameter; Curvature 774
11.4 Motion Along a Curve 785
11.5 Integrals of Vector Functions; Projectile Motion 796
11.6 Application: Kepler’s Laws of Planetary Motion 801
Chapter Review 805
Chapter Project: How to Design a Safe Road 807
12 Functions of Several Variables 809
12.1 Functions of Two or More Variables and Their Graphs 810
12.2 Limits and Continuity 819
12.3 Partial Derivatives 829
12.4 Differentiability and the Differential 840
12.5 Chain Rules 849
Chapter Review 858
Chapter Project: Searching for Exoplanets 861
13 Directional Derivatives, Gradients, and Extrema 862
13.1 Directional Derivatives; Gradients 863
13.2 Tangent Planes 875
13.3 Extrema of Functions of Two Variables 879
13.4 Lagrange Multipliers 891
Chapter Review 899
Chapter Project: Measuring Ice Thickness on Crystal Lake 901
14 Multiple Integrals 903
14.1 The Double Integral over a Rectangular Region 904
14.2 The Double Integral over Nonrectangular Regions 911
14.3 Double Integrals Using Polar Coordinates 923
14.4 Center of Mass; Moment of Inertia 929
14.5 Surface Area 936
14.6 The Triple Integral 941
14.7 Triple Integrals Using Cylindrical Coordinates 950
14.8 Triple Integrals Using Spherical Coordinates 956
14.9 Change of Variables Using Jacobians 962
Chapter Review 968
Chapter Project: The Mass of Stars 971
15 Vector Calculus 973
15.1 Vector Fields 974
15.2 Line Integrals 977
15.3 Fundamental Theorem of Line Integrals 989
15.4 An Application of Line Integrals: Work 1002
15.5 Green’s Theorem 1008
15.6 Parametric Surfaces 1016
15.7 Surface and Flux Integrals 1027
15.8 The Divergence Theorem 1037
15.9 Stokes’ Theorem 1045
Chapter Review 1053
Chapter Project: Modeling a Tornado 1056
16 Differential Equations 1058
16.1 Classification of Ordinary Differential Equations 1059
16.2 Separation of Variables in First-Order Differential Equations 1062
16.3 Exact Differential Equations 1072
16.4 First-Order Linear Differential Equations; Bernoulli Differential Equations 1077
16.5 Power Series Methods 1089
Chapter Review 1094
Chapter Project: The Melting Arctic Ice Cap 1096
APPENDIX A Precalculus Used in Calculus A-1
A.1 Algebra Used in Calculus A-1
A.2 Geometry Used in Calculus A-11
A.3 Analytic Geometry Used in Calculus A-16
A.4 Trigonometry Used in Calculus A-25
A.5 Sequences; Summation Notation; the Binomial Theorem A-38
APPENDIX B Theorems and Proofs B-1
B.1 Limit Theorems and Proofs B-1
B.2 Theorems and Proofs Involving Inverse Functions B-3
B.3 Derivative Theorems and Proofs B-4
B.4 Integral Theorems and Proofs B-8
B.5 A Bounded Monotonic Sequence Converges B-11
B.6 Taylor’s Formula with Remainder B-12
Answers AN-1
Photo Credits PC-1
Index IN-1