11.4 Area and Arc Length in Polar Coordinates
Integration in polar coordinates involves finding not the area underneath a curve but, rather, the area of a sector bounded by a curve as in Figure 11.35. Consider the region bounded by the curve \(r = f(\theta)\) and the two rays \(\theta = \alpha\) and \(\theta = \beta\) with \(\alpha \lt \beta\). To derive a formula for the area, divide the region into \(N\) narrow sectors of angle \(\Delta\theta = ({\beta - \alpha})/N\) corresponding to a partition of the interval \([\alpha,\beta]\): \[ \theta_0 = \alpha \lt \theta_1 \lt \theta_2 \lt \cdots \lt \theta_N = \beta \]
635
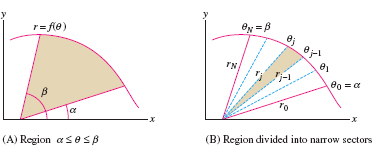
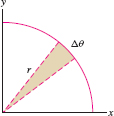
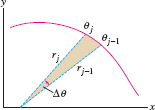
Recall that a circular sector of angle \(\Delta \theta\) and radius \(r\) has area \(\frac12r^2\Delta\theta\) (Figure 11.36). If \(\Delta\theta\) is small, the \(j\)th narrow sector (Figure 11.37) is nearly a circular sector of radius \(r_j = f(\theta_j)\), so its area is approximately \(\frac12r_j^2\Delta\theta\). The total area is approximated by the sum: \begin{equation} \label{12.polarea.rsum} \textrm{Area of region}\approx\sum_{j = 1}^N \frac12r_j^2 \Delta\theta = \frac12\sum_{j = 1}^N f(\theta_j)^2 \Delta\theta\tag{1} \end{equation}
This is a Riemann sum for the integral \({\displaystyle\frac12\int_{\alpha}^{\beta} f(\theta)^2\, d\theta}\). If \(f(\theta)\) is continuous, then the sum approaches the integral as \(N\to\infty\), and we obtain the following formula.
THEOREM 1
Area in Polar Coordinates If \(f(\theta)\) is a continuous function, then the area bounded by a curve in polar form \(r = f(\theta)\) and the rays \(\theta = \alpha\) and \(\theta = \beta\) (with \(\alpha \lt \beta\)) is equal to \begin{equation} \label{12.polarea.formula}\boxed{\bbox[#fef7e5,5pt]{ \frac12 \int_{\alpha}^{\beta} r^2 \, d\theta = \frac12 \int_{\alpha}^{\beta} f(\theta)^2 \, d\theta}}\tag{2} \end{equation}
We know that \(r = R\) defines a circle of radius \(R\). By Eq. (2), the area is equal to \(\displaystyle\frac12\int_0^{2\pi}R^2\,d\theta = \frac12R^2(2\pi)=\pi R^2\), as expected.
EXAMPLE 1
Use Theorem 1 to compute the area of the right semicircle with equation \(r = 4\sin\theta\).
REMINDER
In Eq. (4), we use the identity \begin{equation} \label{12.polarea.trigid} \sin^2\theta = \frac12(1 - \cos 2\theta)\tag{3} \end{equation}
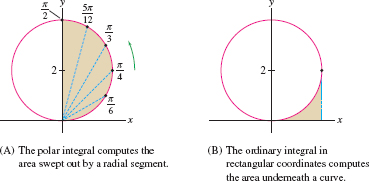
Solution The equation \(r = 4\sin\theta\) defines a circle of radius 2 tangent to the \(x\)-axis at the origin. The right semicircle is “swept out” as \(\theta\) varies from 0 to \(\frac{\pi}2\) as in Figure 11.38. By Eq. (2), the area of the right semicircle is \begin{align} \frac12\int_0^{\pi/2} r^2\,d\theta & = \frac12 \int_0^{\pi/2} (4\sin\theta)^2 \, d\theta = 8\int_0^{\pi/2} \sin^2\theta\,d\theta\tag{4}\\ &=8\int_0^{\pi/2} \frac12 (1-\cos2\theta)\, d\theta\notag\\ &= (4\theta - 2\sin 2\theta)\bigg\vert_0^{\pi/2} = 4\left(\frac{\pi}{2}\right) - 0 = 2\pi \notag \end{align}
636
CAUTION
Keep in mind that the integral \({\frac12\int_\alpha^\beta r^2\,d\theta}\) does not compute the area under a curve as in Figure 11.38, but rather computes the area “swept out” by a radial segment as \(\theta\) varies from \(\alpha\) to \(\beta\), as in Figure 11.38.
EXAMPLE 2
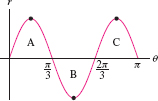
Sketch \(r = \sin 3\theta\) and compute the area of one “petal.”
Solution To sketch the curve, we first graph \(r = \sin 3\theta\) in rectangular coordinates. Figure 11.39 shows that the radius \(r\) varies from \(0\) to \(1\) and back to \(0\) as \(\theta\) varies from \(0\) to \(\frac{\pi}{3}\). This gives petal A in Figure 11.40. Petal B is traced as \(\theta\) varies from \(\frac{\pi}{3}\) to \(\frac{2\pi}{3}\) (with \(r \leq 0\)), and petal C is traced for \(\frac{2\pi}{3} \le \theta\le \pi\). We find that the area of petal \(A\) (using Eq. (3) in the margin of the previous page to evaluate the integral) is equal to \[ \frac12\int_0^{\pi/3} (\sin 3\theta)^2\,d\theta = \frac12\int_0^{\pi/3} \left(\frac{1-\cos 6\theta}2 \right) \,d\theta = \left(\frac14 \theta - \frac1{24}\sin 6\theta \right)\bigg|_0^{\pi/3} = \frac{\pi}{12} \]

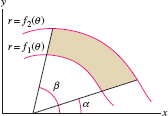
The area between two polar curves \(r = f_1(\theta)\) and \(r = f_2(\theta)\) with \(f_2(\theta)\ge f_1(\theta)\), for \(\alpha\le \theta\le \beta\), is equal to (Figure 11.41): \begin{equation} \boxed{\bbox[#fef7e5,5pt]{ \textrm{Area between two curves} = \frac12\int_\alpha^\beta \big(f_2(\theta)^2 - f_1(\theta)^2\big)\,d\theta}}\tag{5} \end{equation}
EXAMPLE 3 Area Between Two Curves
Find the area of the region inside the circle \(r = 2\cos \theta\) but outside the circle \(r = 1\) [Figure 11.42].
Solution The two circles intersect at the points where \((r, 2\cos\theta)= (r, 1)\) or in other words, when \(2\cos\theta = 1\). This yields \(\cos\theta = \frac12\), which has solutions \(\theta = \pm\frac{\pi}3\).
637

We see in Figure 11.42 that region (I) is the difference of regions (II) and (III) in Figure 11.42 and Figure 11.42. Therefore, \begin{align} \textrm{Area of (I)} &= \textrm{area of (II)} - \textrm{area of (III)}\notag\\ &=\frac12\int_{-\pi/3}^{\pi/3} (2\cos \theta)^2\, d\theta - \frac12\int_{-\pi/3}^{\pi/3} (1)^2\, d\theta\notag\\ &=\frac12 \int_{-\pi/3}^{\pi/3} (4\cos^2 \theta-1)\, d\theta =\frac12 \int_{-\pi/3}^{\pi/3} (2\cos2\theta+1)\,d\theta\tag{6} \\ &= \frac12(\sin2\theta + \theta)\bigg|_{-\pi/3}^{\pi/3} = \frac{\sqrt{3}}2+\frac{\pi}3\notag \end{align}
REMINDER
In Eq. (6), we use the identity \[ \cos^2\theta=\frac12(1+\cos2\theta) \]
We close this section by deriving a formula for arc length in polar coordinates. Observe that a polar curve \(r = f(\theta)\) has a parametrization with \(\theta\) as a parameter: \[ x = r\cos\theta = f(\theta)\cos\theta,\qquad y = r\sin\theta = f(\theta)\sin\theta \]
Using a prime to denote the derivative with respect to \(\theta\), we have \begin{align*} x'(\theta)= \frac{dx}{d\theta} =-f(\theta)\sin\theta + f'(\theta)\cos\theta\\ y'(\theta) = \frac{dy}{d\theta} = f(\theta)\cos\theta+f'(\theta)\sin\theta \end{align*}
Recall from Section 11.2 that arc length is obtained by integrating \({\sqrt{x'(\theta)^2 + y'(\theta)^2}}\). Straightforward algebra shows that \({x'(\theta)^2 + y'(\theta)^2 = f(\theta)^2 + f'(\theta)^2}\), and thus \begin{equation} \label{12.polar.polararc} \boxed{\bbox[#fef7e5,5pt]{\textrm{Arc length \(s\)} = \int_{\alpha}^{\beta} \sqrt{ f(\theta)^2 + f'(\theta)^2} \, d\theta }}\tag{7} \end{equation}
EXAMPLE 4
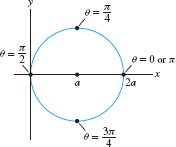
Find the total length of the circle \(r = 2a\cos\theta\) for \(a > 0\).
Solution In this case, \(f(\theta) = 2a\cos\theta\) and \[ f(\theta)^2 + f'(\theta)^2 = 4a^2\cos^2 \theta + 4a^2\sin^2 \theta = 4a^2 \]
The total length of this circle of radius \(a\) has the expected value: \[ \int_0^{\pi} \sqrt{f(\theta)^2 + f'(\theta)^2} \, d\theta = \int_0^{\pi} (2a)\, d\theta = 2\pi a \]
Note that the upper limit of integration is \(\pi\) rather than \(2\pi\) because the entire circle is traced out as \(\theta\) varies from \(0\) to \(\pi\) (see Figure 11.43).
11.4.1 Summary
638
- Area of the sector bounded by a polar curve \(r = f(\theta)\) and two rays \(\theta = \alpha\) and \(\theta = \beta\) (Figure 11.44): \[ \mathrm{Area} = \frac12\int_{\alpha}^{\beta} f(\theta)^2\, d\theta \]
- Area between \(r=f_1(\theta)\) and \(r=f_2(\theta)\), where \(f_2(\theta)\ge f_1(\theta)\) (Figure 11.45):
\[
\mathrm{Area} = \frac12\int_{\alpha}^{\beta} \bigl(f_2(\theta)^2 - f_1(\theta)^2\bigr)\,
d\theta
\]
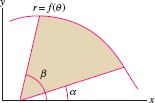 Figure 11.44: Region bounded by the polar curve \(r=f(\theta)\) and the rays \(\theta=\alpha\), \(\theta=\beta\).
Figure 11.44: Region bounded by the polar curve \(r=f(\theta)\) and the rays \(\theta=\alpha\), \(\theta=\beta\).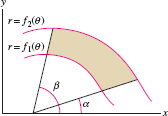 Figure 11.45: Region between two polar curves.
Figure 11.45: Region between two polar curves. - Arc length of the polar curve \(r = f(\theta)\) for \(\alpha\le \theta \le \beta\): \[ \textrm{Arc length} = \int_{\alpha}^{\beta} \sqrt{f(\theta)^2 + f'(\theta)^2}\, d\theta \]