Limits

2.5 More On Evaluating Limits Algebraically

Substitution can be used to evaluate limits when the function in question is known to be continuous. For example, \(f(x) = x^{-2}\) is continuous at \(x=3\), and therefore,\[\lim\limits_{x\rightarrow 3} x^{-2} = 3^{-2} = \frac{1}{9}\]

When we study derivatives in Chapter 3, we will be faced with limits \(\lim\limits_{x\rightarrow c}f(x)\), where \(f(c)\) is not defined. In such cases, substitution cannot be used directly. However, many of these limits can be evaluated if we use algebra to rewrite the formula for \(f(x)\).

To illustrate, consider the limit (Figure 2.32).\[\lim\limits_{x\rightarrow 4}\frac{x^2-16}{x-4}\]

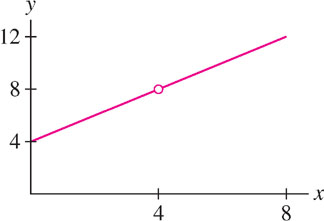
Figure 2.32: Graph of \(f(x) = \frac{x^2-16}{x-4}\). This function is undefined at \(x=4\), but the limit as \(x\rightarrow 4\) exists.

The function \(f(x) = \frac{x^2-16}{x-4}\) is not defined at \(x=4\) because the formula for \(f(4)\) produces the undefined expression \(\tfrac{0}{0}\). However, the numerator of \(f(x)\) factors: \[\frac{x^2 - 16}{x-4} = \frac{(x + 4)(x - 4)}{x-4} = x+4 \text{ (valid for } x\neq 4\text{)}\]

This shows that \(f(x)\) coincides with the continuous function \(x+4\) for all \(x\neq 4\). Since the limit depends only on the values of \(f(x)\) for \(x\neq 4\), we have\[\lim\limits_{x\rightarrow 4}\frac{x^2-16}{x-4} = \underbrace{\lim\limits_{x\rightarrow 4} x + 4 = 8}_{\text{Evaluate by substitution}}\]

Question 2.15 More on Limits Progress Check 1

Determine \(\lim\limits_{x\rightarrow 1} \frac{x^2 - 4}{x+2}\)	UYinCekNO0E=
Determine \(\lim\limits_{x\rightarrow -2} \frac{x^2 - 4}{x+2}\)	sWNiRN4ZHUU=

Correct.

Incorrect.

Try again. Apply the appropriate rule. Think what is allowed and what is needed.

We say that \(f(x)\) has an indeterminate form (or is indeterminate) at \(x=c\) if the formula for \(f(c)\) yields an undefined expression of the type \[\frac{0}{0},\frac{\infty}{\infty},\infty\cdot0,\infty-\infty\]

Other indeterminate forms are \(1^\infty, \infty^0\) and \(0^0\). These are treated in Section 4.5.

Our strategy, when this occurs, is to transform \(f(x)\) algebraically, if possible, into a new expression that is defined and continuous at \(x=c\), and then evaluate the limit by substitution (“plugging in”). As you study the following examples, notice that the critical step is to cancel a common factor from the numerator and denominator at the appropriate moment, thereby removing the indeterminacy.

Example 1

Calculate \(\lim\limits_{x\rightarrow 3}\dfrac{x^2-4x+3}{x^2+x-12}\).

Solution The function has the indeterminate form \(\tfrac{0}{0}\) at \(x=3\) because \[\begin{aligned}\text{Numerator at } x=3: & \quad x^2-4x+3 = 3^2 - 4(3) + 3 = 0\\ \text{Denominator at } x=3: & \quad x^2 + x - 12 = 3^2 + 3 - 12 = 0\end{aligned}\]

Step 1. Transform algebraically and cancel. \[\frac{x^2-4x+3}{x^2+x-12} = \underbrace{\frac{(x-3)(x-1)}{(x-3)(x+4)}}_{\text{Cancel common factor}} = \underbrace{\frac{x-1}{x-4}}_{\stackrel{\scriptstyle\text{Continuous}}{\text{at } x=3}} \quad\text{(if } x\neq 3 \text{)}\tag{1}\]

Step 2. Substitute (evaluate using continuity).

Because the expression on the right in Eq. (1) is continuous at \(x=3\), \[\lim\limits_{x\rightarrow 3}\frac{x^2-4x+3}{x^2+x-12} = \underbrace{\lim\limits_{x\rightarrow 3} \frac{x-1}{x+4} = \frac{2}{7}}_{\text{Evaluate by substitution}}\]

Question 2.16 More on Limits Progress Check 2

jZlJh1ycnDoLjqiIR/4zYIzWa6WZL5khtdRXJSzwoaSCoU+gn62C0dSC1zSJEgKoazsAEgvqh3Nk/INUr5nlWg==

Correct.

Recall from algebra that a difference of cubes can be factored as \(a^3-b^3=(a-b)(a^2+ab+b^2)\).

Incorrect.

Example 2 The Form \(\tfrac{\infty}{\infty}\)

Calculate \(\lim\limits_{x\rightarrow \frac{\pi}{2}} \dfrac{\tan x}{\sec x}\).

Solution As we see in Figure 2.33, both \(\tan x\) and \(\sec x\) have infinite discontinuities at \(x=\frac{\pi}{2}\), so this limit has the indeterminate form \(\frac{\infty}{\infty}\) at \(x=\frac{\pi}{2}\).

Figure 2.33: ---

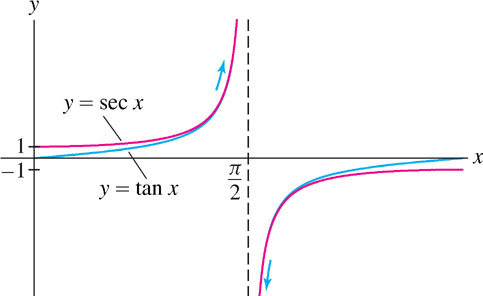
Step 1. Transform algebraically and cancel. \[\frac{\tan x}{\sec x} = \frac{\sin x \left(\frac{1}{\cos x}\right)}{\frac{1}{\cos x}} = \sin x \quad \text{(if }\cos x \neq 0\text{)}\]

Step 2. Substitute (evaluate using continuity).

Because \(\sin x\) is continuous, \[\lim\limits_{x\rightarrow \frac{\pi}{2}} \dfrac{\tan x}{\sec x} = \lim\limits_{x\rightarrow \frac{\pi}{2}} {\sin x} = 1\]

Question 2.17 More on Limits Progress Check 3

Kk3nJex/L7gkI81Wtq25Fj2BGdxv0jmpxk+4087NLQ4vkjBW/NTwfmvgMDDTpsKiWQcD/LpQijdHxG+jlW3gaSE6jnNfuV5c5/aXB1eDUMVaz/bZxSfdZuKIwuIW/yA2

Correct.

Rewrite \(\tan x\) as \(\tfrac{\sin x}{\cos x}\) and reduce the resulting complex fraction. This should set you up for using substitution.

Incorrect.

Example 3 The Form \(\infty - \infty\)

Calculate \(\lim\limits_{x\rightarrow 1}\left(\dfrac{1}{x-1} - \dfrac{2}{x^2 - 1}\right)\).

Solution As we see in Figure 2.34, \(\frac{1}{x-1}\) and \(\frac{2}{x^2-1}\) both have infinite discontinuities at \(x=1\), so this limit has the indeterminate form \(\infty - \infty\).

Figure 2.34: ---

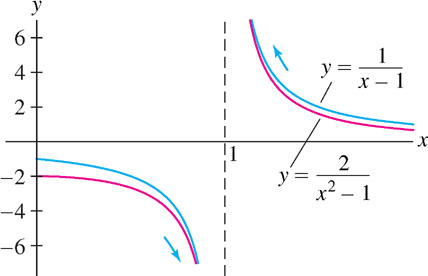
Step 1. Transform algebraically and cancel.

Combine the fractions and simplify (for \(x\neq 1\)): \[\dfrac{1}{x-1} - \dfrac{2}{x^2 - 1} = \dfrac{x + 1}{x^2-1} - \dfrac{2}{x^2 - 1} = \dfrac{x - 1}{x^2-1} = \dfrac{1}{x+1}\]

Step 2. Substitute (evaluate using continuity). \[\lim\limits_{x\rightarrow 1}\left(\dfrac{1}{x-1} - \dfrac{2}{x^2 - 1}\right) = \lim\limits_{x\rightarrow 1} \frac{1}{x+1} = \frac{1}{1+1} = \frac{1}{2}\]

Question 2.18 More on Limits Progress Check 4

AV9rY2ZiOhCOemx+LHA2laR54Y9Im22UZV2Vnvi8PdxlN43zkcUBMy5TgZVJtZcRKucxNH0tgGDKYs0p3IAioZfoIazcGEyG2NUnQmOwKXduDSaV1vfCGJP2SFA4d6uSe77O3Z/yrfH/iD6G

Correct.

Try again.It may seem counter-intuitive, but it helps to factor \(x-4\) as \((\sqrt x -2)(\sqrt x +2)\) and then combine the expressions.

Incorrect.

In the next example, the function has the undefined form \(\tfrac{a}{0}\) with \(a\) nonzero. This is not an indeterminate form (it is not of the form \(\tfrac{0}{0},\tfrac{\infty}{\infty}\) etc.).

Example 4 Infinite But Not Indeterminate

Evaluate \(\lim\limits_{x\rightarrow 2}\dfrac{x^2 - x + 5}{x-2}\).

Solution The function \(f(x) = \frac{x^2 - x + 5}{x-2}\) is undefined at \(x=2\) because the formula for \(f(2)\) yields \(\tfrac{7}{0}\): \[\begin{aligned}\text{Numerator at } x=2: & \quad x^2-x+5 = 2^2 - 2 + 5 = 7\\ \text{Denominator at } x=2: & \quad x-2 = 2 - 2 = 0\end{aligned}\]

But \(f(x)\) is not indeterminate at \(x=2\) because \(\tfrac{7}{0}\) is not an indeterminate form. Figure 2.35 suggests that the one-sided limits are infinite: \[\lim\limits_{x\rightarrow 2^-}\frac{x^2 - x + 5}{x-2} = -\infty \qquad \lim\limits_{x\rightarrow 2^+}\frac{x^2 - x + 5}{x-2} = \infty\]

Figure 2.35: Graph of \(f(x) = \frac{x^2 - x + 5}{x-2}\).

The limit itself does not exist.

We conclude this section with a comment on Example 3 in Section 2.2. In that example we used algebra to reinvestigate Example 1 in Section 2.2. It should now be clear that multiplying numerator and denominator with the conjugate of the denominator allows one to rewrite the expression in such a way to remove the indeterminacy and then use substitution to evaluate the limit directly.

2.5.1 Section 2.5 Summary

When \(f(x)\) is known to be continuous at \(x=c\), the limit can be evaluated by substitution: \(\lim\limits_{x\rightarrow c} f(x) = f(c)\).
We say that \(f(x)\) is indeterminate (or has an indeterminate form) at \(x=c\) if the formula for \(f(c)\) yields an undefined expression of the type \[\frac{0}{0},\frac{\infty}{\infty}, \infty\cdot 0, \infty - \infty\]
If \(f(x)\) is indeterminate at \(x=c\), try to transform \(f(x)\) algebraically into a new expression that is defined and continuous at \(x=c\). Then evaluate by substitution.